Расчёт на жёсткость

Деформацию балки (углы поворота поперечных сечений и прогибы) исследуем с помощью универсальных уравнений метода начальных параметров. С этой целью расчётную схему представим в соответствующем виде (рис. 4.).

Рис. 4. Расчётная схема балки к составлению универсального уравнения

изогнутой оси балки

Записываем в общем виде универсальное дифференциальное уравнение изогнутой (упругой) оси балки – одно для всех участков:

2. Первое интегрирование дифференциального уравнения даёт уравнение углов поворота поперечных сечений:

3. Интегрирование уравнения углов поворота поперечных сечений даст уравнение прогибов:

4. Начальные параметры EI_xy₀ и EI_x θ₀ находим из граничных условий (условий закрепления балки):

а) при z=2 м прогиб на опоре 2 равен нулю (конец участка I), т.е.

б) при z=7 м прогиб на опоре 4 равен нулю (конец участка II) т.е.

в) решая систему уравнений

получим: EI_xθ₀=2,5 кН∙м²; EI_xy₀= 21,667 кН∙м³.

5. Универсальные уравнения углов поворота поперечных сечений и прогибов с учётом найденных начальных параметров и значений нагрузки балки примут вид:

6. Эпюры углов поворота поперечных сечений и прогибов строим по значениям, вычисленным в отдельных сечениях балки с интервалом Δz=1 м. Результаты расчётов сводим в табл. 1.

Таблица 1

Z, м	0,0	1,0	2,0	3,0	4,0	5,0	6,0	7,0	8,0
EIxθ, кН∙м2	2,5	-7,5	-37,5	-30,8	-4,2	22,5	27,5	2,5	-17,5
EIxy, кН∙м3	21,67	20,84	0,0	36,66	55,00	45,00	17,50	0,0	-10,83

Покажем, например, вычисления угла поворота и прогиб сечения балки на расстоянии z=6 м (участок III).

Эпюры EI_xθ и∙EI_xy для удобства анализа необходимо изобразить на одном рисунке под расчётной схемой (рис.5.

20

*

*

Эпюра М_и, кН∙м

10

40

40

*

Эпюра EI_xθ, кН∙м²

*

*

*

*

4,12 м

Эпюра EI_xy, кН∙м³

*

*

*

*

*

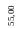
EI_xy_max=55,28

Рис.5. Эпюры изгибающих моментов, углов поворота поперечных сечений и прогибов

На эпюрах EI_xθ и∙EI_xy «звёздочкой» отмечены особые точки – экстремальные значения, точки смены кривизны (точки перегиба). Положения этих точек определяются из дифференциально-интегральных зависимостей между «θ» и «y» и на основании закона Гука при изгибе. Студенту необходимо знать и использовать эти зависимости для полного представления о деформации балки.

Экстремальное значение прогиба в нашем примере по эпюре EI_xy, (оно же и максимальное по модулю) в сечении на расстоянии z=4,12 м (участок II) (положение сечения определено графически, при условии вычерчивания (а не рисования!) всех эпюр с учётом принятых масштабов).

Максимальный (по абсолютной величине – модулю) прогиб стальной балки – (двутавр № 22; Е=2·10⁵ МПа, I_x=2550 см⁴)

Здесь учтён перевод единиц измерений:

|EI_xy_max|=55,28·кН·м³=55,28·10⁶ кН·см³; Е=2·10⁵ МПа =2·10⁴ кН/см².

Условие жёсткости не удовлетворяется, т.к. значит необходимо увеличить жёсткость балки.

Из условия жёсткости получим

Этому условию удовлетворяет двутавр № 24 (I_x=3460 см⁴).

В результате расчётов на прочность и жёсткость принимае

поперечное сечение балки – двутавр № 24