§ 27. Расчет изгибаемых элементов
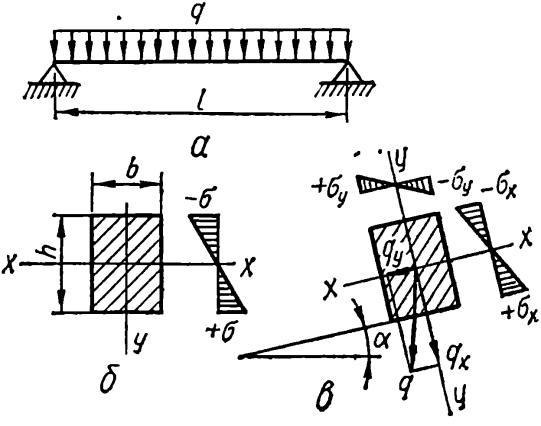
Изгибаемые деревянные элементы — настилы, обрешетки, обшивки, стропильные ноги, прогоны, балки — наиболее распространенные элементы деревянных зданий и сооружений. Поэтому рациональное проектирование их с полным использованием несущей способности ведет к значительной экономии лесоматериала. Балки цельного сечения менее чувствительны к порокам древесины и поэтому их разрешается выполнять из древесины II категории. Различают два вида работы элементов на изгиб — (рис. 41, а); простой изгиб, когда нагрузка действует в плоскости одной из главных осей инерции поперечного сечения элемента(рис. 41, б); косой изгиб, когда направление нагрузки не совпадает ни с одной из главных осей инерции сечения (рис. 41, в).
Расчет элементов на прочность при простом изгибе производится по формуле:
,
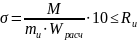где где М — расчетный изгибающий момент,
кН
см;
- коэффициент
условий
работы элемента при изгибе, принимаемый
равным 1, за
исключением
случаев введения поправок на форму и
размеры сечения (например
и
для расчета клееных прямолинейных и
гнутых
элементов);
—
расчетный момент сопротивления (по
площади
нетто)
рассматриваемого поперечного сечения,
;
—
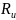расчетное
сопротивление
материала изгибу, МПа. Подбор сечения
по заданному расчетному изгибающему
моменту М при простом изгибе производится
по формуле:
.
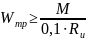По
найденному моменту сопротивления
находятся размеры поперечного сечения
и подбирается пиломатериал по сортименту.
Например, для прямоугольного сечения:
.
Пиломатериал
подбирается так, чтобы принятое сечение
имело
.
Расчет элементов на прочность по нормальным напряжениям при косом изгибе производится по формуле:
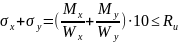(ф.30),
где
—
соответствующие моментам
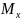и
напряжения изгиба;
и
— составляющие расчетного изгибающего
момента относительно главных осей х и
у;
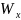и
— расчетные моменты
сопротивления
рассматриваемого поперечного сечения
для осей х
и
y;
— расчетное сопротивление материала
изгибу. Для подбора сечения при косом
изгибе формулу (ф.30) можно преобразовать:
.
(ф.31)
Здесь:
,
если сечение прямоугольное и пролеты
изгибаемого элемента относительно
осей х и у одинаковы. Подставляя эти
величины в формулу
(ф.31)
и решая ее относительно
получим:
.
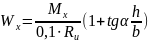Расчет изгибаемых элементов на скалывание производится в местах наибольших поперечных сил (обычно — возле опор) по формуле:
,
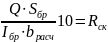где
Q — расчетная поперечная сила в данном
сечении, кН;
,
и
,
— статический момент брутто и момент
инерции брутто
сдвигаемой
части сечения относительно нейтральной
оси;
—
расчетная
ширина сечения, см;
— расчетное сопротивление материала
скалыванию при изгибе, МПа. Проверка
на скалывание при изгибе цельных
деревянных элементов может оказаться
решающей для коротких балок
с большими нагрузками или для балок с
двумя сосредоточенными силами
возле
опор. Для балок цельного сечения
покрытий и перекрытий зданий с равномерной
нагрузкой проверку на скалывание можно
не проводить.
Проверка
жесткости изгибаемого элемента
состоит в определении
наибольшего
изгиба от нормативных нагрузок и в
сопоставлении его
с
предельно допустимым. Обычно прогиб
вычисляется как относительная величина
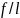в предположении упругой работы
древесины.
Влиянием касательных напряжений на
прогиб балок прямоугольного сечения
обычно пренебрегают и учитывают его
лишь
при
расчете клеенодощатых балок таврового
сечения с тонкими стенками. Вычисление
прогибов производится по формулам
сопротивления
материалов
в соответствии с расчетными схемами.
Для балок симметричного сечения в
плоскости изгиба прогибы можно находить
по обобщенной формуле:
,(ф.34), где
— максимальное напряжение от нормативной
нагрузки, МПа;
k
— коэффициент, зависящий от условий
опирания и нагрузки; находится по
справочной литературе, например, для
балки на двух
опорах
при равномерной нагрузке k = 5/24; для
такой же балки
со
сосредоточенной силой по середине
пролета k = 1/6 и т. д. При подборе сечения
по условию жесткости необходимую
высоту
балки
получаем из выражения (ф.34), приравнивая
его предельному
прогибу:
.
Заменяем
напряжения от нормативной нагрузки на
напряжения от
расчетной
нагрузки
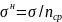(здесь
— усредненный коэффициент
перегрузки).
Тогда при полном использовании прочности
материала —
,
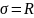получим оптимальную высоту поперечного
сечения балки (ф.36):
. Проверка жесткости при косом изгибе
производится по полному
прогибу,
равному геометрической сумме прогибов
:
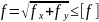,где
— прогиб относительно оси х;
— прогиб относительно оси у. Косой
изгиб всегда вызывает увеличение
размеров изгибаемых элементов, поэтому
следует стремиться к его исключению
или ограничению, например, постановкой
тяжей в плоскости ската крыши по середине
пролета прогонов, уменьшая тем самым
в два раза расчетный
пролет
в плоскости ската.