Теорія ймовірностей та математична статистика
2.1. Для руйнування моста достатньо влучення однієї авіаційної бомби. Знайти ймовірність того, що міст буде зруйновано, якщо на нього скинули 3 бомби та ймовірності влучення яких відповідно дорівнюють 0,6; 0,7 та 0,9.
2.2. Деталь може надійти для обробки на перший верстат з ймовірністю 0,8, а на другий верстат – з ймовірністю 0,2. При обробці деталі на першому й другому верстатах імовірність допустити брак відповідно дорівнює 0,01 і 0,02. Оброблені деталі складають в одному приміщенні. Навмання взята деталь виявилась бракованою. Знайти ймовірність того, що вона оброблялась на першому верстаті.
2.3. За даним законом розподілу дискретної випадкової величини Х
Х |
3 |
4 |
7 |
9 |
12 |
14 |
р |
0,1 |
0,3 |
0,2 |
0,05 |
0,15 |
0,2 |
побудувати многокутник розподілу. Знайти і
2.4. Випадкова величина Х задана функцією розподілу ймовірностей
Потрібно: а) знайти щільність розподілу ймовірностей
б) побудувати графіки функцій і
в) знайти і дисперсію випадкової величини Х;
г) знайти ймовірність
того, що в результаті проведення
випробування випадкова величина набуде
значення з інтервалу
2.5. В результаті вибіркового аналізу добової кількості аварій водопровідної системи на території району одержали певну вибірку
1 0 2 4 0
0 2 3 0 5
2 6 1 5 2
1 0 2 3 1
3 2 4 2 5
Для цієї вибірки потрібно:
а) побудувати дискретний розподіл частот; б) побудувати полігон частот;
в) знайти вибіркову середню ; г) знайти виправлену вибіркову дисперсію ;
д) знайти емпіричну функцію розподілу і побудувати її графік.
Варіант № 6
1. Інтегральне числення функції однієї змінної
1.1. Обчислити інтеграли безпосереднім інтегруванням або внесенням під знак диференціала:
1.
;
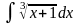2.
;
3.
;
4.
;
5.
;
6.
;
7.
; 8.
;
9.
;
10.
.
1.2.
Обчислити невизначені інтеграли. а)
б)
в)
г)
д)
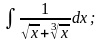е)
1.3. Обчислити визначені інтеграли інтегруванням частинами або методом заміни змінної:
а)
б)
1.4.
Знайти площу фігури, обмежену кривими
і прямою
Теорія ймовірностей та математична статистика
2.1. Кожен із трьох стрільців виконує один постріл по мішені. Ймовірності їхнього влучення в мішень відповідно дорівнюють 0,6; 0,7 та 0,8. Знайти ймовірність того, що результатом цих трьох пострілів буде тільки: а) одне влучення; б) хоча б одне влучення.
2.2.Проростання насіння становить 60%. Яка ймовірність того, що з чотирьох посіяних насінин зійде дві?
2.3. За даним законом розподілу дискретної випадкової величини Х
Х |
-5 |
-4 |
0 |
1 |
2 |
4 |
р |
0,15 |
0,2 |
0,25 |
0,2 |
0,15 |
0,05 |
побудувати многокутник розподілу. Знайти і
2.4. Випадкова величина Х задана функцією розподілу ймовірностей
Потрібно: а) знайти щільність розподілу ймовірностей
б) побудувати графіки функцій і
в) знайти і дисперсію випадкової величини Х;
г) знайти ймовірність
того, що в результаті проведення
випробування випадкова величина набуде
значення з інтервалу
2.5. В результаті вибіркового аналізу добової кількості аварій водопровідної системи на території району одержали певну вибірку
2 4 6 4 5
3 2 5 3 2
0 4 3 4 4
4 1 6 2 6
0 2 2 4 4
Для цієї вибірки потрібно:
а) побудувати дискретний розподіл частот;
б) побудувати полігон частот;
в) знайти вибіркову середню ;
г) знайти виправлену вибіркову дисперсію ;
д) знайти емпіричну функцію розподілу і побудувати її графік.
Варіант № 7
1. Інтегральне числення функції однієї змінної
1.1. Обчислити інтеграли безпосереднім інтегруванням або внесенням під знак диференціала:
1.
;
2.
;
3.
; 4.
;
5.
;
6.
;7.
;
8.
;
9.
; 10.
; 1.2.
Обчислити невизначені інтеграли. а)
б)
в)
г)
д)
е)
1.3. Обчислити визначені інтеграли інтегруванням частинами або методом заміни змінної:
а)
б)
1.4.
Знайти площу фігури, обмежену лінією
і віссю
