5. Расчет компенсатора на жесткость и прочность

Перемещение в месте стыка трубопровода и компенсатора зависит от жесткости компенсатора, которая определяется его геометрическими параметрами Жесткость компенсатора в свою очередь подбирается в зависимости от продольных перемещений и продольных сил, которые возникают от перепада температур и внутреннего давления.

Поэтому на практике параметры компенсаторов подбирают методом последовательных приближений.

В начале жесткость компенсатора принимается равной нулю и определяются перемещения . Исходя из необходимости компенсировать перемещения, определяют параметры и далее жесткость компенсатора.

После этого вновь вычисляют перемещения , но уже с учетом жесткости компенсатора.

Таким образом, после нескольких приближений определяют окончательные параметры компенсатора.

Главной, практически важной характеристикой компенсатора является его жесткость , которая является обратной величиной податливости .

Определение податливости и жесткости П-образного компенсатора.

На рисунке 42 изображена схема П-образного компенсатора. Необходимо определить его податливость и жесткость.

Конструкция компенсатора представляет собой систему, состоящую из круговых отводов и прямолинейных участков труб.

По определению податливостью компенсатора в заданной точке и в заданном направлении является перемещение от единичной силы , в этом направлении.

Компенсатор П-образной формы на расчетной схеме рассматривается , как стержневая система, состоящая из круговых (1, 3-ий) и прямолинейных (2, 4-ый) участков).

Для определения перемещения используем известный из курса сопротивления материалов метод Мора (10.2). Интеграл Мора для П-образного компенсатора примет вид

, (10.3)

где - суммарная длина всех участков, прямолинейных и круговых;

- осевой момент инерции сечения трубы, определяемый по формуле

. (10.4)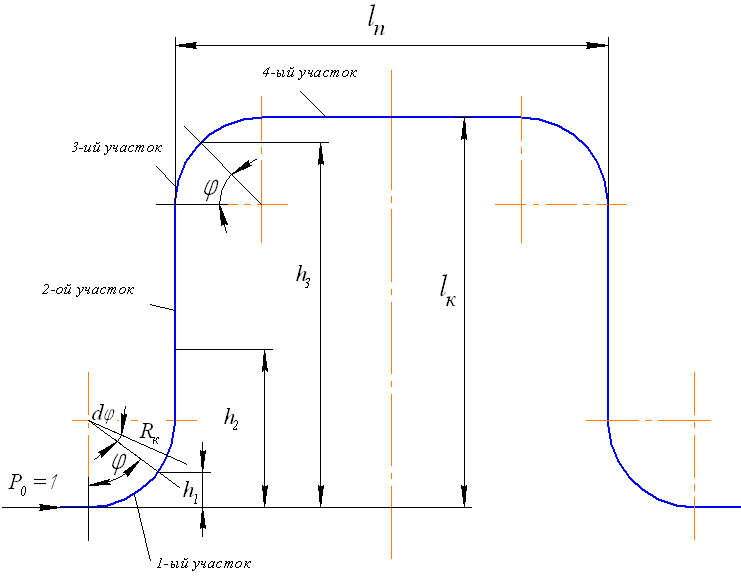

Рисунок 42. Расчетная схема П-образного компенсатора.

С учетом симметрии компенсатора получается следующее выражение для его податливости

, (10.5)

где - определенные интегралы, вычисленные на соответствующих участках.

Рассмотрим, как вычисляется определенный интеграл на первом участке. Изгибающий момент в поперечных сечениях кругового участка компенсатора от единичной силы вычисляется, как произведение единичной силы на плечо (рисунок 42).

(10.6)

Для кругового участка компенсатора удобнее перейти к полярным координатам, тогда

, (10.7)

. (10.8)

После этого получаем интеграл

. (10.9)

После интегрирования получаем следующий результат

. (10.10)

Для второго участка

Для третьего участка

.

.(10.12)

Для половины четвертого участка

. (10.13)

Полученные выражения нужно умножить на 2, чтобы получить полную податливость компенсатора.

Расчет на прочность П-образного компенсатора.

Если в месте примыкания трубопровода к компенсатору в продольном направлении определено перемещение , тогда можно найти отпор компенсатора по формуле

(10.19)

Зная отпор компенсатора, можно найти максимальный изгибающий момент, который будет возникать в сечении наиболее удаленном от линии действия силы отпора компенсатора

(10.20)

Максимальное продольное напряжение, возникающее в месте перехода отвода компенсатора к полочке компенсатора, необходимо вычислять с учетом коэффициента концентрации напряжений

(10.21)

. (10.22)

Если дополнительно учесть все возможные напряжения, которые могут возникнуть в наиболее опасном месте компенсатора, получим выражение по СНиП 2.05.06-85 «Магистральные трубопроводы»

, (10.23)

где - расчетное сопротивление материала компенсатора;

- дополнительные продольные напряжения в компенсаторе от изгиба под действием поперечных и продольных нагрузок (усилий) в расчетном сечении компенсатора.