Лекция № 4 основы моделирования строительных конструкцийи и сооружений

Моделирование является одним из основных видов испытаний конструкций, проводимых с исследовательской целью. Несмотря на то, что наиболее полную информацию о работе конструкций можно получить в процессе натурных испытаний, их проведение во многих случаях сопряжено с большими материальными затратами и непреодолимыми трудностями методического характера. К таким трудностям относится достижение в натурных условиях требуемой точности измерений или исключение влияющих факторов, т. е. обеспечение проведения контролируемого эксперимента. При моделировании можно выделить лишь основные факторы, изучение которых является целью данного эксперимента, и при построении модели предусмотреть варьирование этих факторов на заданных уровнях. Кроме того, в лабораторных условиях намного проще обеспечить требуемую точность измерений всех изучаемых параметров.

Следует отметить, что испытание в лаборатории конструкций, например, фермы пролетом 24 м или плиты перекрытия 3х12 м, также относится к моделированию в масштабе 1:1, поскольку в этом случае нагружение и опирание конструкций моделируются. Вместе с тем, испытания моделей во многом дополняют натурные испытания. Так, изучение воздействий на сооружения кранов, технологического оборудования, ветра и т.д. может быть выполнено только в реальных условиях. Но тщательное изучение распределения воздействия между элементами сооружения успешно изучается на моделях, например, при продувке высотных конструкций в аэродинамической трубе или при генерировании морского волнения в лотках.

4.1. Классификация видов подобия при моделировании

Моделированием называется метод исследования строительных конструкций и сооружений на их моделях с использованием определенных законов подобия процессов и явлений, протекающих в натурных конструкциях и в моделях.

Использование для испытаний в исследовательских целях конструкций натуральных размеров связано с большими материальными и трудовыми затратами. Испытания на модели или на разных моделях различными методами позволяют быстрее, всесторонне и более дешевым способом получить необходимые сведения.

Не следует смешивать понятие моделирования с макетированием строительной конструкции. Макеты создают для наглядности компоновочного или конструктивного решения объекта, чаще всего для демонстрационных целей. Моделирование является методом экспериментально-теоретического исследования объекта.

Моделирование включает следующие операции: построение модели, изучение свойств этой модели при заданных условиях или воздействиях и перенос полученных сведений на моделируемый объект. Моделирование рассматривает только подобные явления и базируется на теории подобия. Параметры, характеризующие подобные явления, связаны между собой определенными преобразованиями, позволяющими от эффектов, изучаемых на модели, перейти к исследуемым явлениям в натуре. В практике моделирования широко используется математическое и физическое подобие.

Математическое подобие может существовать между явлениями разной физической природы, но описываемыми тождественными уравнениями. Например, уравнение Лапласа описывает распределение суммы главных напряжений в плоской задаче теории упругости; этим же уравнением определяется электрический потенциал на каждой точке плоского проводника, к которому подведен ток. Таким образом, измерение физической величины – электрического потенциала – позволяет исследовать распределение механических напряжений. На этом принципе основаны модели-аналоги, представляющие собой электрические цепи замещения, сеточные интеграторы, а также аналоговые машины непрерывного действия.

Физическое подобие требует полного или частичного воспроизведения физических процессов, протекающих в натурном объекте. При этом натура и модель являются одинаковыми по физической природе: соответственные величины модели и натуры отличаются лишь количественно, но не качественно.

Физическое подобие является основой механического моделирования. С использованием принципов механического моделирования решаются две основные задачи: замена расчета внутренних усилий в элементах конструкций определением напряженно-деформированного состояния идеализированных моделей и моделирование действительной работы конструкций в неупругой и предельной стадии нагружения.

Поскольку моделирование базируется на теории подобия, рассмотрим принципы получения условий подобия.

Различают три основных вида моделирования - механическое, математическое и физическое.

Механическое моделирование использует законы механического подобия процессов, протекающих в твердых деформируемых телах равных масштабов. В зависимости от поставленной задачи возможны три направления механического моделирования.

Первое - испытание моделей с целью проверки достоверности методов расчета, в соответствии с которыми запроектирована модель. В этом случае сама модель по отношению к проверяемому аналитическому аппарату является натурной конструкцией. Размеры модели в этом случае не имеют значения, важно лишь, чтобы они соответствовали расчёту и могли быть исполнены при ее изготовлении.

Главная задача такого испытания - оценить пригодность аналитического аппарата, использовавшегося при расчёте, и в случае необходимости внести в него уточнения. При этом вес явления, которые проявляются в модели, точно так же будут иметь место и в натурной конструкции, рассчитанной таким же методом. В этом случае никакого пересчёта результатов испытания с модели на натуру не требуется. Эффективность и целесообразность такого вида моделирования заключается в том, что изготовить малоразмерную модель и провести ее испытание легче, дешевле и быстрее, чем крупноразмерную натурную конструкцию. При необходимости испытание модели проще повторить.

Второе направление - исследование конструкций или процессов, которые не имеют аналитического описания, не имеют методики расчета. В этом случае вместо аналитического расчёта производят испытание модели, исследуют проявляющиеся закономерности, выявляют предельные состояния. Результаты испытания используют затем для разработки методов расчёта аналогичных конструкций.

Второе направление моделирования особенно важно для железобетонных конструкций, методы расчёта которых базируются на закономерностях деформирования в стадии предельного равновесия, эти закономерности, в свою очередь, могут быть выявлены и изучены только при испытаниях натурных конструкций или их моделей.

Третье направление механического моделирования - исследование на модели процессов с целью переноса результатов испытания на натурную конструкцию. В этом случае масштаб модели, её элементов, механические характеристики материалов подбирают по определенным законам подобия.

Математическое моделирование

Сущность его заключается в том, что процессы, протекающие в натурной конструкции при определенной схеме нагружения, описываются математически и исследуются аналитическими методами. Этот вид моделирования требует привлечения соответствующих методов теории сооружений и сопряжён, как правило, с необходимостью решения достаточно большого числа уравнений.

Для математического моделирования сложных многократно статически неопределимых конструкций наиболее подходящим в настоящее время признан метод конечных элементов (МКЭ), изучаемый в курсе строительной механики. Сущность его заключается в том, что многоэлементные дискретные конструкции и континуальные системы разделяют на элементы, работа которых в статическом смысле приближенно или точно изучена. Напряжённо-деформированное состояние смежных конечных элементов сопрягают между собой так, чтобы удовлетворялись условия равновесия и совместности деформаций.

На базе МКЭ были разработаны и нашли широкое применение в проектной практике мощные программы для ЭВМ, например программно-вычислительные комплексы ЛИРА разных модификаций. Эти комплексы позволяют исследовать напряжённо-деформированное состояние практически любых конструкций надземных и подземных сооружений в упругой стадии работы при линейном законе деформирования.

Математическое моделирование особенно удобно при многовариантном проектировании или при исследовании влияния разных переменных параметров на работу конструкции.

Математическое моделирование может использоваться в сочетании с механическим как метод расчёта, требующий экспериментальной проверки на физических моделях.

Физическое моделирование

В основе его лежит использование известных аналогий, наблюдающихся при математическом описании процессов разной физической природы. Так, например, в основе всех зависимостей теории упругости лежит, как известно, обобщенный закон Гука, который при одноосном напряженном состоянии связывает напряжение и деформацию стержня с механической константой материала зависимостью:

σ= Е·ε (4.1)

В электротехнике основным является закон Ома V = R·I, который связывает напряжение и силу тока в проводнике с физической константой проводника R. Каждый курсант или студент без труда заметит также существование аналогий между известными уравнениями статического равновесия фрагментов механических систем и законами Кирхгофа, характеризующими равновесие тока во фрагментах электрических цепей. В недалеком прошлом на базе этих аналогий создавались электрические модели - аналоги для исследований соответствующих механических систем. В настоящее время метод физического моделирования уступает место названному выше методу конечных элементов.

Сущность механического моделирования. Понятие о теории подобия

Подобными в механическом смысле называют такие деформируемые системы, которые являются подобными геометрически и у которых напряжения, деформации, перемещения и другие исследуемые величины в сходственных точках в сходные моменты времени могут быть выражены через определенные соотношения, называемые масштабами перехода.

Теория подобия, лежащая в основе механического моделирования, изучает закономерности соотношений между геометрическими размерами прототипа исследуемой конструкции, так называемой натуры, и её модели, механическими константами материалов, величинами нагрузок, напряжениями и деформациями прототипа и модели.

Условия подобия, согласно этой теории, устанавливают двояким образом. Первый заключается в анализе размерностей величин, относящихся к исследуемому процессу. Если прототип или исследуемый процесс мало изучены, то можно составить для них только перечень описывающих параметров, характеризующих этот процесс и имеющих одинаковые размерности, как у прототипа, так и у его модели. Второй способ исходит из анализа уравнений, описывающих данный процесс, рассматривает поведение объекта при различных воздействиях с учётом реальных граничных условий. Этот способ считается более корректным. В последующем мы познакомимся с каждым из названных способов и убедимся, что результаты, определяющие условия подобия, в конечном счёте получаются одинаковыми.

Вспомним основные параметры, которые в общем случае могут входить в уравнение равновесия и влияют на напряжённо-деформированное состояние конструкций в стадии упругой работы. В квадратных скобках покажем символически их размерность, например, для всех линейных величин l_i[L], для сосредоточенных и любых продольных сил P_j[P], модулей упругости E_i [PL^-2] - размерность напряжения и т. д.

Геометрию конструкции, ее элементов характеризуют линейные размеры l_i [L] и соотношения между ними. Основными видами нагрузок могут быть - P_j[P] сосредоточенные силы; M_i[PL] - сосредоточенные моменты; q_i[PL^-1] - погонная (распределенная по длине); q_i[PL^-1] - распределенная по поверхности конструкции.

Механические свойства упругих материалов характеризуются модулями упругости E_i[PL^-2] и коэффициентами Пуассона µ_i, которые не имеют размерности. Относительные фибровые деформации ε_i, также величины безразмерные.

Общим недостатком представления моделируемых параметров в размерном виде является то, что численные величины и соотношения между ними изменяются в зависимости от принятой системы единиц - СИ, метрической или какой-нибудь иной. Поэтому в дальнейшем, ради удобства анализа, от размерных параметров перейдем к безразмерным.

В зависимости от сложности задач, решаемых методом моделирования, и принятых исходных предпосылок различают два вида подобия - простое, или строгое, и расширенное, или неполное. Различия между ними, достоинства и недостатки каждого отметим, ознакомившись с их особенностями.

Простое подобие упругих деформируемых систем. Метод анализа размерностей

Среди приведенных выше параметров, имеющих размерность, в качестве независимых общих удобно принять два, например l и Е, и через них путём анализа размерностей и простых преобразований перейти к безразмерным комплексам. Обязательным условием простого (строгого) подобия является равенство всех полученных таким образом безразмерных комплексов для прототипа и модели. Их одинаковость математически обозначают словом idem, что в переводе с латинского означает «одинаковый», «один и тот же». В такой форме совокупность критериев подобия модели и прототипа приобретает вид:

в отношении геометрии l = idem;

в отношении материалов Е = idem; µ = idem;

в отношении деформации ε = idem;

в отношении нагрузок получим безразмерные комплексы:

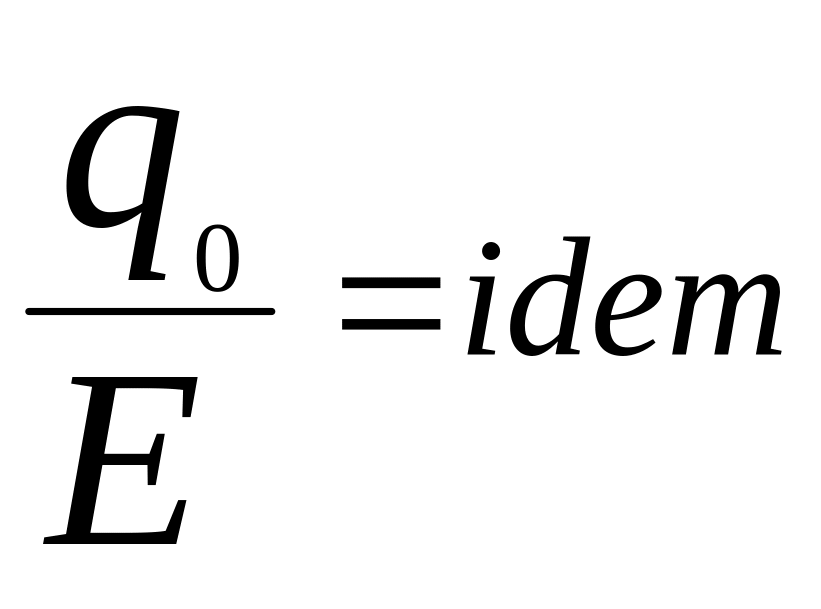; ; ; (4.2)

Критерий подобия l= idem означает, что модель в отношении геометрии должна быть подобна прототипу, т. е. все размеры модели и прототипа должны быть связаны единым масштабным множителем

. (4.3)

Критерии подобия безразмерных параметров µ = idem и ε = idem означают, что в сходственных точках модели и прототипа они должны быть одинаковыми, т. е.

; . (4.4)

Для линейного упругого материала это означает равенство отношений:

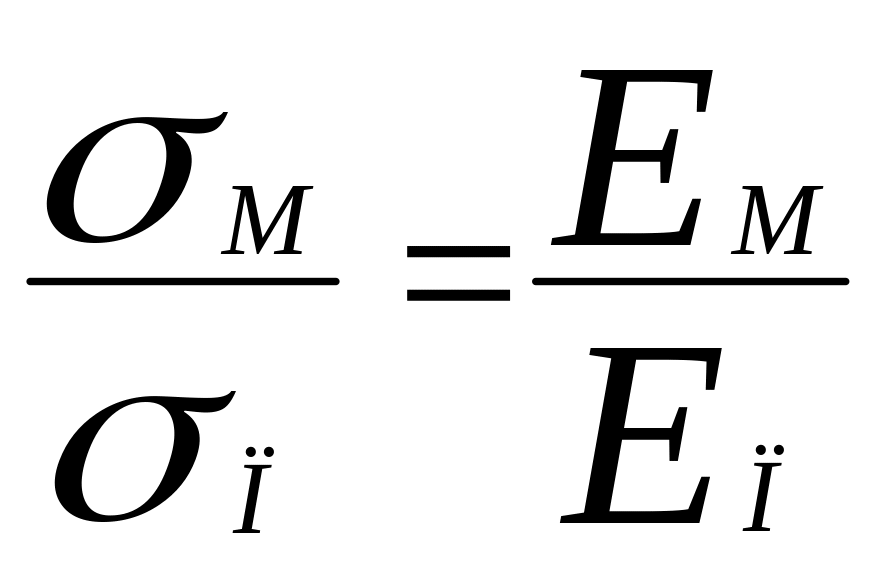или (4.5)

Эти и другие безразмерные отношения целесообразно заменить соответствующими масштабными множителями. Так, зависимости (4.4) и (4.5) можно записать в следующем виде:

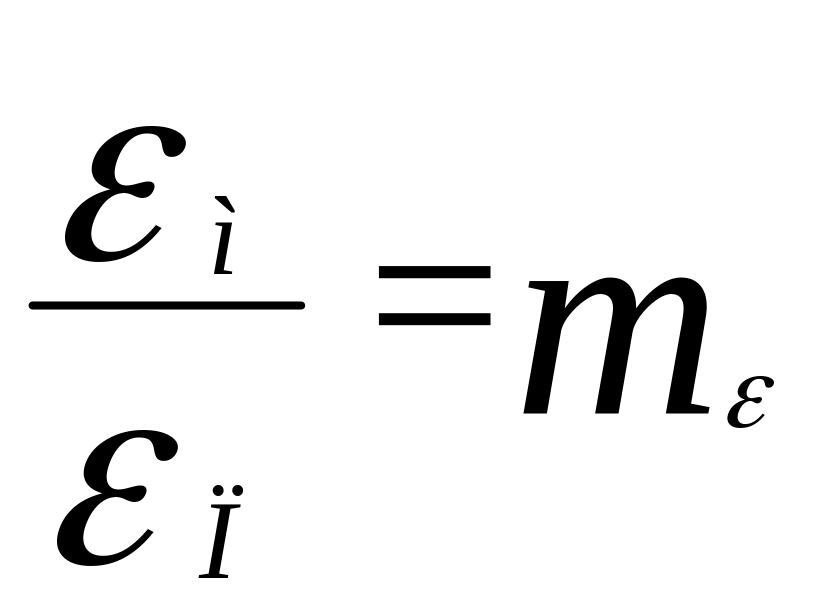; ; ; (4.6)

Из этих отношений, с учетом (4.4) и (4.5), получим:

; ; (4.7)

Соотношения вида (4.7) называются индикаторами подобия. При простом подобии все критерии подобия idem, выраженные через масштабные коэффициенты, также являются индикаторами подобия, равными единице, т. е.:

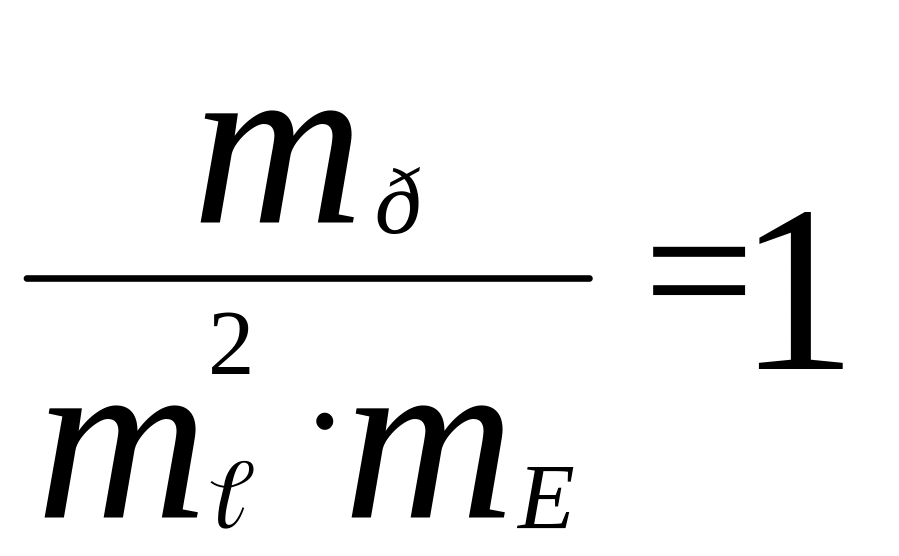; ; ; . (4.8)

Индикаторы (4.8) имеют важное значение, так как с их помощью находят соотношение между нагрузками, действующими на прототип и на модель в любых комбинациях. Рассмотрим некоторые частные случаи. Допустим, что масштабы т_l и т_E известны, т. е. размеры модели и материал, из которого она будет изготовлена, даны. Требуется рассчитать нагрузку на модель, а если нагрузки разные, то соотношение между ними.

Случай 1. К прототипу приложены только сосредоточенные силы Р_1П, Р_2П„ и т. д. Чему должны быть равны Р_1M; P_2M и т.д. в сходственных точках модели, чтобы выполнялись все критерии подобия?

Воспользуемся первым индикатором подобия (4.8), найдем т_р=т_Е·m²_l , а затем, зная т_р , определим P_iМ = P_iН ·т_р . Из последнего выражения следует также, что при нагружении модели на всех стадиях следует соблюдать закон пропорциональности и синхронности изменения нагрузок. Аналогично решается задача относительно любой схемы нагружения, предусмотренной индикаторами (4.8).

Случай 2. К прототипу приложены одновременно сосредоточенные силы P_1П, P_2П и погонные распределенные нагрузки q_1П, q_2П и т. д. Каково должно быть соотношение между интенсивностями нагрузок на модель, чтобы соблюдались все критерии подобия?

Из равенства левых частей первого и третьего критериев подобия (4.8) находим взаимосвязь m_p = m_q m_l .

Установив масштаб т_р без учета т_q, как в случае 1, находим m_q = т_р /т_l, а затем и сами нагрузки q_lM=q_iПm_q Аналогично решается задача при любом сочетании нагрузок.

Определение индикаторов подобия методом анализа уравнений

Сущность метода рассмотрим на примере балки, нагруженной произвольной нагрузкой и испытывающей поперечный изгиб.

Воспользуемся уравнением изогнутой оси балки в общем виде:

. (4.9)

Очевидно, что это уравнение в равной мере описывает закон деформирования, как прототипа, так и его модели. При этом подобие деформации и усилий будет обеспечено, если в обоих уравнениях будет соблюдено соотношение сходственных величин, т. е. их масштабов. Опустив дифференциальные операторы и заменив параметры всех величин их масштабами, получим уравнение:

. (4.10)

Изгибающие моменты в правой части уравнения (4.9) могут быть заменены сводными функциями от конкретной нагрузки на балку. Так, например, при любой погонной нагрузке q(x) можно представить уравнение изгибающих моментов в виде:

. (4.11)

Заменив конкретные параметры масштабами преобразований, получим уравнение:

. (4.12)

В этом уравнении опущен масштаб т_k, который равен единице, поскольку является отношением равных чисел.

Масштабы линейных преобразований принимаем одинаковыми по всем направлениям, а именно m_х = m_v = m_z =m_l, тогда m₁ = т_l⁴ (так как размерность момента инерции см⁴). Подставив в (4.10), с учетом (4.12), получим:

(4.13)

или окончательно:

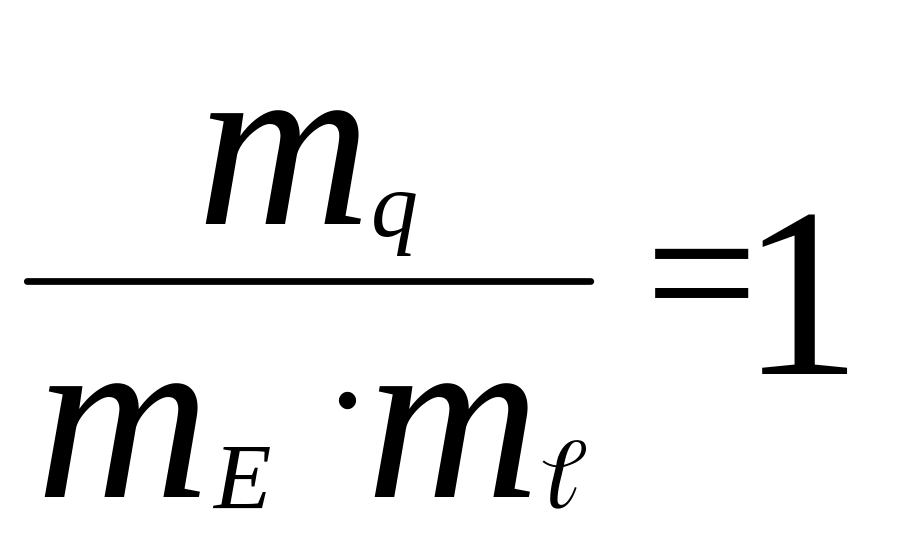. (4.14)

Полученный индикатор подобия при распределенной нагрузке q(x) в точности совпадает с аналогичным в формуле (4.8), полученным методом анализа размерностей.

Если балка нагружена сосредоточенными силами Р_i, то функцию изгибающих моментов можно представить в виде уравнения:

. (4.15)

Заменив конкретные параметры их масштабам, учитывая, что т_k=1, сделав преобразования уравнения (4.10) аналогично предыдущему, получим критерий подобия:

, (4.16)

который в точности совпадает с аналогичным в формуле (4.8). К такому же выводу мы придем, рассматривая конструкции, нагруженные поверхностной нагрузкой, если будем оставаться в пределах гипотез простого подобия.

В заключение еще раз сформулируем необходимые и достаточные условия простого подобия при моделировании задач теории упругости:

1. модель и прототип должны быть геометрически подобными;

2. коэффициенты Пуассона для материала модели и материала прототипа должны быть равны;

3. материал модели должен быть упругим, его выбор обусловливает значение масштаба модулей;

4. все нагрузки на модель должны находиться в таком же соотношении между собой, как и соответствующие нагрузки, действующие на прототип;

5. поскольку масштаб т_Е определен выбором материала для модели, то для произвольного выбора остаются только масштабы т_l либо масштаб одной из нагрузок, например т_p , остальные вычисляют, используя индикаторы подобия.

Расширенное подобие и его особенности

Условия простого (строгого) моделирования с соблюдением полного геометрического и механического подобия содержат набор индикаторов, одновременное выполнение которых подчас вызывает значительные трудности либо оказывается вообще невозможным. В таких случаях приходится идти на неполное, расширенное подобие.

При расширенном подобии ставится ограниченная задача: точно моделируются не все исследуемые параметры, а лишь некоторые, важнейшие, характеризующие исследуемый процесс.

К ним в первую очередь относятся напряжения в контрольных точках. Другие параметры, например деформации, могут не моделироваться или оцениваться приближённо. В тех же случаях, когда необходимо установить картинку перемещения характерных точек или распределение усилий между элементами, можно отказаться от строгого геометрического подобия и моделировать, например, жёсткости соответствующих элементов, от которых главным образом зависят перемещения, а напряжения оценивать приближённо.

Моделирование при неполном расширенном подобии покажем на примерах отдельных видов строительных конструкций.

Тонкие пластинки постоянной или переменной толщины h

Моделирование их с соблюдением полного геометрического подобия затруднительно, так как оказывается сложно исполнить модель с малой толщиной h_м, кроме того, с уменьшением толщины снижается достоверность результатов измерений при испытании, а следовательно, и результатов испытаний в целом. В таких случаях толщину пластинки моделируют в масштабе m_h , отличном от масштаба т_l. Масштабы преобразований основных параметров при этом будут иметь следующие значения. Если коэффициенты Пуассона прототипа и модели равны µ_м = µ_п , то масштаб напряжений будет равен:

; (4.17)

масштаб деформаций:

; (4.18)

масштаб прогибов:

. (4.19)

При µ_п ≠ µ_м деформации моделируются в масштабах:

; (4.20)

прогибы в масштабе:

(4.21)

При моделировании безмоментных оболочек, толщина которых также мала, линейный масштаб т_l серединой поверхности и толщины m_h также могут не совпадать. При выборе материала модели стремятся, чтобы µ_п = µ_м . Масштаб нагрузок назначают из условия:

. (4.22)

Другие виды нагрузки моделируют с соблюдением индикаторов подобия (4.8). Компоненты напряжений при этом будут моделироваться в масштабе:

; (4.23)

деформации в масштабе:

; (4.24)

перемещения в масштабе:

. (4.25)

Моментные оболочки постоянной и переменной толщины следует моделировать с соблюдением условий полного геометрического подобия и нагрузок.

В заключение отметим, что описанные выше методы простого и расширенного подобия дают лишь общее представление о принципиальной сущности исследования строительных конструкций на механических моделях, приведенные сведения не могут рассматриваться как исчерпывающие. При необходимости решения конкретных практических и исследовательских задач требуется более глубокое изучение данного вопроса с привлечением специальной литературы.

Моделирование железобетонных конструкций. Цели и задачи моделирования

В экспериментально-теоретических исследованиях железобетонных конструкций моделирование имеет важное значение. В первую очередь это относится к большепролетным пространственным конструкциям перекрытий и покрытий, которые в настоящее время широко применяют в мировой строительной практике. Для них характерно практически неограниченное многообразие геометрических форм и конструктивных решений. Однако расчёт таких конструкций по предельным состояниям в ряде случаев вызывает серьезные затруднения. Это связано с тем, что создание методик расчёта, аналитических выражений, определяющих условия надёжности, предполагает, что все возможные для данной конструкции предельные состояния, все возможные схемы разрушения и деформации известны. Однако выявлены они могут быть только экспериментально по результатам испытаний, как правило, не одной, а нескольких моделей или натурных конструкций.

В отдельных случаях проектирование пространственных конструкций производят, опираясь на результаты приближенного расчёта, например методом конечных элементов (МКЭ), который, как известно, построен на базе зависимостей теории упругости. Применительно к конструкциям из железобетона, особенно в стадии работы с трещинами, запроектированные конструкции обязательно проверяют испытанием их моделей.

Для получения надежных экспериментальных данных модель должна проектироваться так, чтобы в ней нашли отражение основные конструктивные особенности прототипа. В частности, если моделируется сборная конструкция, элементы которой соединены закладными деталями и шпоночными бетонными швами, то эти особенности должны быть учтены и в модели.

Размеры модели, её масштаб назначают с учётом многих факторов, как-то: наличие стационарных стендов и их размеры, способ нагружения и силовое оборудование, удобство расстановки приборов и доступ к ним. Но главным является размер исследуемой конструкции-прототипа, поскольку толщина поля оболочек и пластинок у модели должна быть не меньше 4-5 мм. Обычно геометрию модели выполняют в едином масштабе от 1:25 до 1:4 по отношению к прототипу.

Материалы для моделей. Индикаторы подобия

Для изготовления моделей применяют мелкозернистый бетон или пескобетон, а в качестве арматуры - стержневую и проволочную арматуру, а также тканые сетки, стандартные или специального изготовления.

Бетон для модели проектируют таким, чтобы модули упругости прототипа и модели на день испытания были примерно равны, т. е. т_Ев = 1. Достичь одновременно с этим подобия по прочности бетона очень трудно, поэтому ограничиваются приближенным совпадением прочностей.

Моделирование рабочей арматуры производят с учётом того, что она включается в работу элементов модели и прототипа после образования трещин в бетоне. При этом продольные арматурные стержни в нормальных сечениях выполняют функцию связей, растянутых сосредоточенными силами N_si=Rsi·Asi или их равнодействующей N_s = ∑ R_si· A_si, а поперечная арматура в наклонных сечениях выполняет функцию распределённых погонных связей с несущей способностью q_Sω = ∑R_Sωi · А_Sωi, где А_Sωi площадь сечения поперечной арматуры, отнесенная к единице длины каркаса (рис. 4.1).

Индикаторы подобия для пересчёта арматуры, по аналогии с индикаторами подобия для нагрузки в виде сосредоточенных сил P_j и погонной распределенной q, согласно формулам (4.8), получают следующий вид:

для продольной арматуры:

, где ; ; (4.26)

в развернутом виде:

. (4.27)

Рассуждая таким же образом, для поперечной арматуры получим зависимость:

(4.28)

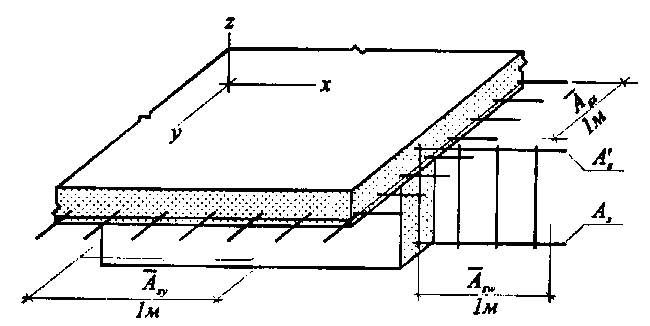
Рис. 4. 1. Обозначения моделируемой арматуры

Моделирование предварительно напряжённых конструкций имеет свои особенности, которые в лекции не рассматриваются.