15. Кореляційний аналіз
Сутність кореляції
Кореляція (від лат. correlatio - співвідношення) - це статистична залежність між випадковими величинами, що носить імовірнісний характер.
Кореляційні зв'язки можна вивчати на якісному рівні з діаграм розсіяння емпіричних значень змінних X і Y і відповідним чином їх інтерпретувати. Так, наприклад, якщо підвищення рівня однієї змінною супроводжується підвищенням рівня іншої, то йдеться про позитивну кореляцію або прямий зв'язок. Якщо ж зростання однієї змінної супроводжується зниженням значень іншої, то маємо справу з негативною кореляцією або зворотним зв'язком. Нульовою називається кореляція за відсутності зв'язку змінних. Проте нульова загальна кореляція може свідчити лише про відсутність лінійної залежності, а не взагалі про відсутність будь якого статистичного зв'язку .
У психолого-педагогічних дослідженнях здебільшого спостерігаються зв'язки нелінійні . Наприклад, зростання мотивації спочатку підвищує ефективність навчення, а потім наступає зниження продуктивності. Кількісна міра кореляційного зв'язку оцінюється за значеннями коефіцієнтами кореляції у межах від -1 до +1. Від'ємні значення коефіцієнтів указують на зворотний зв'язок, додатні - на прямий. Нульове значення може свідчити про відсутність зв'язку. Інтенсивність зв'язку (слабкий зв'язок - помірний - суттєвий - сильний) оцінюється за абсолютним значенням коефіцієнтів кореляції.
Лінійна кореляція
Лінійний кореляційний зв'язок для емпіричних даних, виміряних за шкалою інтервалів або відношень, оцінюється за допомогою коефіцієнта кореляції Пірсона гху
де Хі і у і - значення змінних X і У; х і у - середні X і У; п - обсяг вибірки.
8 Зазначені методи розрахунку з використанням комп'ютерної техніки можна знайти у підручнику [56].
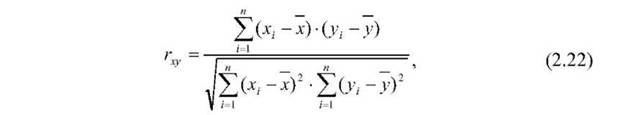
Автокореляція
Автокореляція або автокореляційна функція - це кореляція функції з самою собою зміщеною на певну величину незалежної змінної. Автокореляція використовується для знаходження закономірностей в ряді даних, таких як періодичність. Часто застосовується у статистиці та обробці сигналів для аналізу функцій або серій даних. Математично автокореляційна функція визначається як:
,
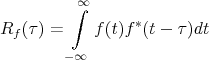де
функція 
інтегрується
у добутку з комплексно спряженою та
зміщеною на певну величину 
(часто
це
час) функцією.
16. Регресі́йний ана́ліз — розділ математичної статистики, присвячений методам аналізу залежності однієї величини від іншої. На відміну від кореляційного аналізу не з'ясовує чи істотний зв'язок, а займається пошуком моделі цього зв'язку, вираженої у функції регресії.
Мета регресійного аналізу
Визначення ступеня детермінованості варіації критеріальної (залежної) змінної предикторами (незалежними змінними).
Пророкування значення залежної змінної за допомогою незалежної.
Визначення внеску окремих незалежних змінних у варіацію залежної.
Регресійний аналіз не можна використовувати для визначення наявності зв'язку між змінними, оскільки наявність такого зв'язку і є передумова для застосування аналізу.
Регресійний аналіз (англ. regression analysis) – це метод визначення відокремленого і спільного впливу факторів на результативну ознаку та кількісної оцінки цього впливу шляхом використання відповідних критеріїв.
Регресійний аналіз проводиться на основі побудованого рівняння регресії і визначає внесок кожної незалежної змінної у варіацію досліджуваної (прогнозованої) залежної змінної величини.
Основним
завданням регресійного аналізу є
визначення впливу факторів на
результативний показник (в абсолютних
показниках). Передусім для цього необхідно
підібрати та обґрунтувати рівняння
зв'язку, що відповідає характеру
аналітичної стохастичної залежності
між досліджуваними ознаками. Рівняння
регресії показує як в середньому
змінюється результативна ознака (
)
під впливом зміни факторних ознак (хі).
У загальному вигляді рівняння регресії можна представити так:
,
де – залежна змінна величина;
х – незалежні змінні величини (фактори).
Залежно від кількості змінних величин виділяють різні види регресійного аналізу. Якщо змінна величина завжди одна, то змінних може бути як одна, так і декілька. Виходячи з цього, виділяють два види регресійного аналізу: парний (простий ) регресійний аналіз і регресійний аналіз на основі множинної регресії, або багатофакторний.
Парний регресійний аналіз – вид регресійного аналізу, що включає у себе розгляд однієї незалежної змінної величини, а багатофакторний – відповідно дві величини і більше.