8.7 Связь между универсальной и удельной газовыми постоянными
Связь между Ср и СV для идеального газа (любой газ до 3 МПа можно условно считать идеальным, а до 50 МПа – с погрешностью) можно определить с помощью уравнения Майера: Ср-СV=R, где СV – удельная изохорная; R –удел. газовая постоянная R=Rμ/μ=8314/μ (Дж/кгК), Ср – удельная изобарная теп-ть.
Rμ-универсальная газовая постоянная
Уравнение Майера через мольную теплоемк.: Сμр- СμV= Rμ=8314, (Дж/КмольК), где Сμр- молярная изобарная; СμV – мольная изохорная.
Уравнение Майера показывает насколько изобарная теплоемкость больше изохорной. Массовая изобарная больше массовой изохорной на величину удельной газовой постоянной. Или молярная изобарная больше молярной изохорной на величину универсальной газовой постоянной.
Показатель адиабаты: К=Ср/СV=Сμр/СμV; Ср>СV в К раз. Например для воздуха К≈1,4 (вообще для 2-х атомных газов). Показатель адиабаты слабо уменьшается с ростом температуры.
8.8 Уравнения состояния идеального и реальных газов
1) уравнение Менделеева–Клапейрона (уравнение состояния идеального газа): Рν=RT,
где Т – абсолютная термодинамическая температура (К); ν - удельный объем:ν=W/m, (м3/кг), где W –объем; m- масса; Р –абсолютное давление (Па);
РW= mRT;
R=Rμ/μ => РW=mTRμ/μ,
где m/μ =N – количество вещества (кмоль);
РW=NRμT=8314NT.
При высоких давлениях или очень низких температурах все газы не подчиняются уравнению Менделеева – Клапейрона, в этом случае используя уравнение состояния реального газа:
1) ур. Ван Дер-Ваальса: (Р+а/v2)(v-b)=RT, где a и b – константы; (а/v2) – поправка на межмолекулярные взаимодействия; b –поправка на собственный объем молекул, а и b эмпирические коэффициенты, вычисляемые по критич.параметрам вещества. Из уравнения Ван Дер-Ваальса для высоких давлений и температур (>2000 K) пренебрегая поправкой (а/v2) получаем уравнение Дюпре: Р((1/ρ)-b)=RT.
2)
Ур. Майера-Богомолова:
,
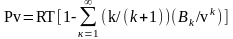для низких давлений, разряжений к=1 =>
,
где Вк
и В1
– эмпирические коэффициенты.
3) ур. Вукаловича-Новикова (Ур. Водяного пара): Рv=RT[1-(A/v)-(B/v2)], где А и В – константы. Для водяного пара составлены таблицы и номограммы.
4) ур. Состояния с вириальными коэффициентами: Pv=Во+(В1/v1)+ (В2/v2),
где Во, В1, В2 – соответственно 0,1,2 – вириальные коэффициенты.
8.9 Изображение процессов в p-V и t-s диаграммах
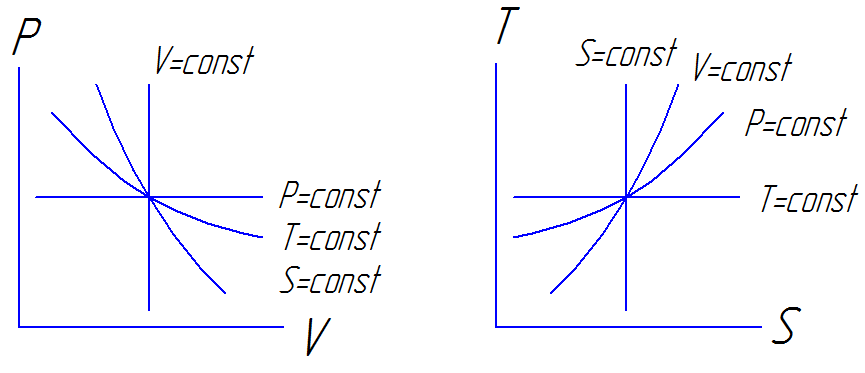
V=const – изохорный процесс
P=const – изобарный процесс
T= const – изотермический процесс
S= const – адиабатный процесс
Работа равна площади под кривой процесса в PV-координатах
Теплота равна площади под кривой процесса в TS-координатах
8.10 Политропный процесс
Политропный процесс – процесс непохожий на не один из простейших, ни один из параметров (Р, Т, S, v) в политропном процессе не является постоянным.
Условились описывать такие процессы уравнения политропы: Pvn=const; В политропном процессе газ считается идеальным, поэтому по аналогии с урпавнениями Пуассона: P1v1n=P2v2n=const, где n –показатель политропы, определяется по спец методике на основе опытных данных. Тvn-1=const; TP-((n-1)/n)=const; Работа: Аn=RT1[1-(P2/P1) (n-1)/n]/(n-1), n=(-∞;+∞). Теплота: Q=Cn(T2-T1), где Cn- удельная теплоемкость политропного процесса:
;
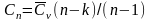Изменение внутренней энергии: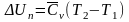
.
я