Задача с2

Плоска рама, що складається з двох тіл, закріплених в точках А, В до нерухомого тіла і з’єднаних в точці С циліндричним шарніром або ковзною муфтою (на схемах рис. С2 умовно показано циліндричний шарнір). Рама навантажена парою сил з моментом М, силами , і розподіленим навантаженням. Визначити реакції опор і зусилля в з’єднанні. Дані наведені в таблиці С2.

Опори, в залежності від конфігурації системи, слід повернути в площині таким чином, щоб збігались дільниці стрижня на схемах опор (див. додаток А) і рами (див. рис. С2).

Момент пари вважається додатним, якщо він намагається повертати раму проти руху годинникової стрілки. Якщо в таблиці стоїть знак мінус, то момент пари направлений за рухом годинникової стрілки.

Вказівка. Задача С2 – на рівновагу системи тіл, на які діє плоска система сил. При її розв’язанні можна спочатку розглянути рівновагу всієї системи в цілому, а потім рівновагу одного з тіл системи, показавши його окремо. Можна розчленити систему на окремі тіла і розглянути рівновагу кожного тіла, враховуючи при цьому третій закон механіки (рівність дії і протидії).

Увага! Систему на окремі тіла можна розчленити тільки по з’єднанні (шарніру або ковзній муфті).

Реакції опор і зусилля в з’єднаннях приведені в додатку А.

Рис. С2.1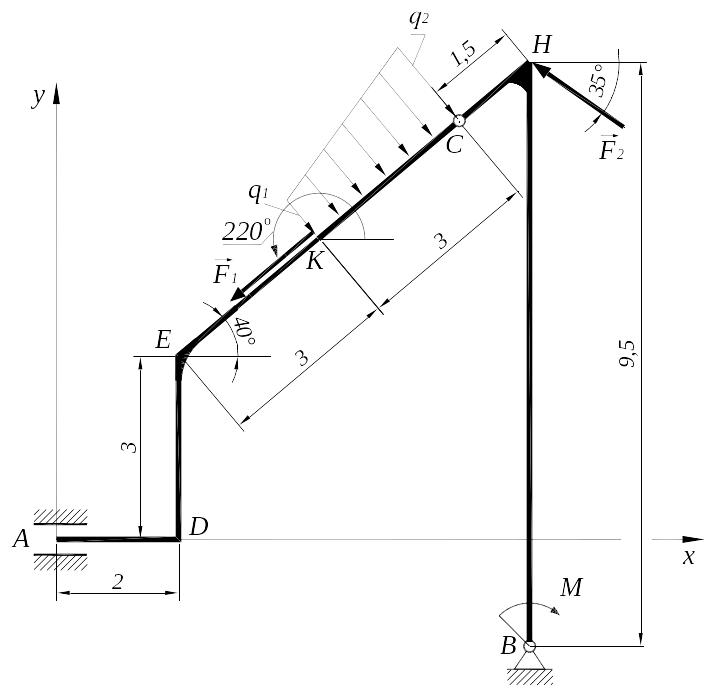

Приклад С2. Плоска рама (рис. С2.1) складається з двох тіл (стрижень і стрижень ) з’єднаних в точці циліндричним шарніром. В точці А рама закріплена напівзащемленою опорою, в точці В – шарнірно нерухомою опорою. На раму в точці К діє сила  кН, , в точці Н – сила  кН, на дільниці СК – розподілене навантаження інтенсивністю  кН/м,  кН/м, на дільниці ВН діє пара сил з моментом  кН·м (напрямленим за рухом годинникової стрілки). Визначити реакції опор А, В і зусилля в з’єднанні С.

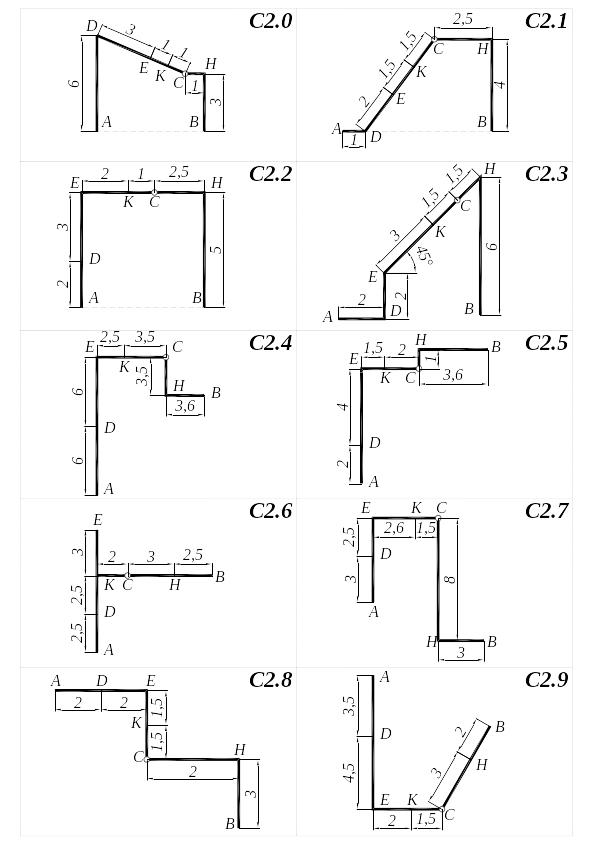
Рис. С2

Таблиця С2

№ рядка	Типи опор в точках		Тип з’єднання в точці С	Сила			Сила			Розподілене навантаження			Пара сил з моментом, М
	А	В		точка при-кладання		модуль сили, кН	точка при-кладання		модуль сили , кН	дільни-ця	модуль q, кН/м	Тип	точка при-кладання	величина кН·м
1			шарнір	С	45	7	D	10	3	KE	4		D	-10
2			ковзна муфта	C	60	8	Е	20	5	HB	6		Е	11
3			шарнір	Е	90	9	К	30	7	DE	q1=4 q2=6		H	12
4			ковзна муфта	К	120	10	Н	40	9	AD	5		С	-13
5			шарнір	Н	135	11	D	50	11	EK	8		Н	-15

Продовження таблиці С2

№ рядка	Типи опор в точках		Тип з’єднання в точці С	Сила			Сила			Розподілене навантаження			Пара сил з моментом, М
	А	В		точка при-кладання		модуль сили, кН	точка при-кладання		модуль сили , кН	дільни-ця	модуль q, кН/м	Тип	точка при-кладання	величина кН·м
6			ковзна муфта	D	150	5	Е	60	13	НC	q1=5 q2=7		C	9
7			шарнір	D	180	4	К	70	15	АD	7		D	-8
8			ковзна муфта	Е	210	3	Н	80	17	DЕ	10		Е	7
9			шарнір	К	225	12	D	45	16	DE	q1=6 q2=10		С	-6
0			ковзна муфта	Н	240	6	Е	90	14	СК	9		С	4

Розв’язання.

1. Розглядаємо окремо рівновагу тіл і . Розчленимо систему по шарніру С.

2. Вибираємо систему координат .

3. Показуємо активні (задані) сили, що діють на стрижень і стрижень . Попередньо розкладаємо їх на складові і , модулі яких дорівнюють

 кН,

 кН,

 кН,

 кН.

Розподілене навантаження замінюємо рівнодійними. Для полегшення обчислень розбиваємо трапецію на прямокутник і трикутник. Модулі рівнодійних для них дорівнюють відповідно

 кН,

 кН.

Розкладаємо сили і на складові, проекції яких дорівнюють

 кН,

 кН,

 кН,

 кН.

4. Відкидаємо в’язі і замінюємо їх реакціями (рис. С2.2, С2.3). В точці А  і , в точці В  і , в шарнірі С  , .

5. На раму діє довільна плоска система сил. Для кожного стрижня можна скласти три рівняння рівноваги, а загальна кількість невідомих – шість. Отже система статично визначна.

6. Складаємо рівняння рівноваги:

Стрижень (рис. С2.2). Використаємо першу форму рівнянь рівноваги:

, (1)

, (2)

. (3)

Рис. С2.2 Рис. С2.3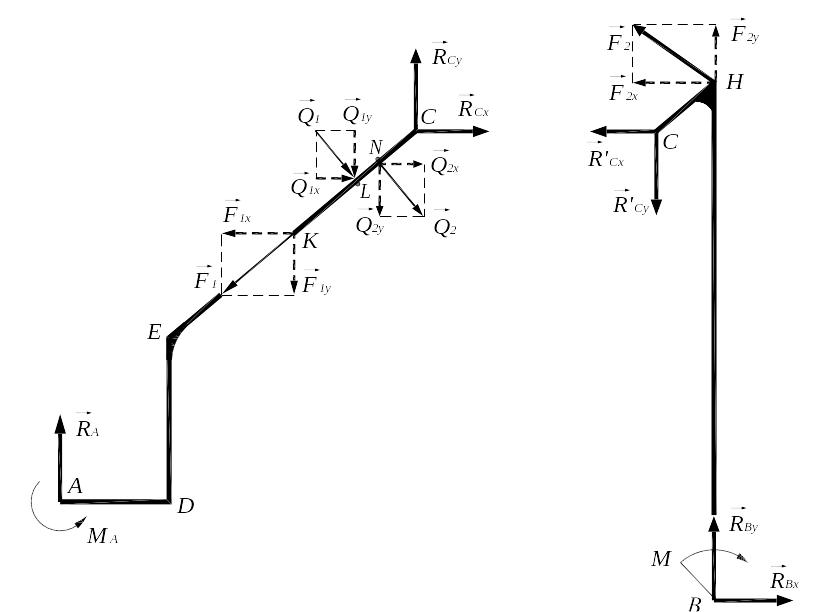

З рівнянь (1) – (3) отримаємо:

,

,

.

Підставимо числові значення і отримаємо

,

, (4)

(5)

Стрижень СНВ (рис. С2.3). Використаємо першу форму рівнянь рівноваги. При цьому врахуємо, що згідно з третім законом механіки . Маємо

, (6)

, (7)

(8)

З рівнянь (6)  (8), поклавши , , отримаємо

,

,

.

Підставимо числові значення. Маємо

,

, (9)

(10)

Підставивши значення в рівняння (10), – в (9), – в (4), а – в (5), отримаємо

,

,

,

Рис. С2.4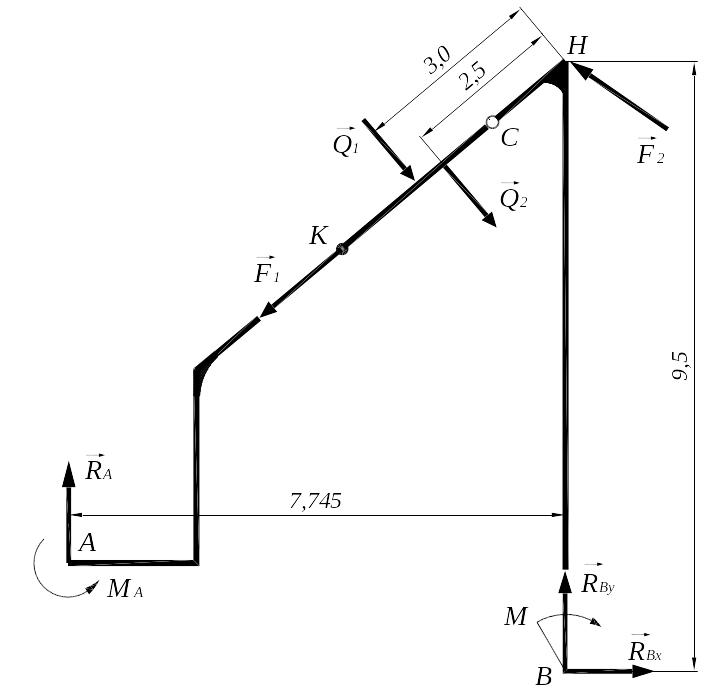

7. Для перевірки правильності визначення опорних реакцій розглянемо рівновагу всієї рами (рис. С2.4). При цьому зусилля в шарнірі С будуть внутрішніми силами і в рівняння рівноваги не ввійдуть. Складемо рівняння рівноваги у вигляді

Оскільки у даному випадку легко обчислювати моменти всіх сил відносно точки С, то сили не розкладаємо на складові. Маємо

Відносна похибка

.

Реакції визначені вірно.

8. Аналіз отриманих результатів.

Знак “мінус” означає, що реакції і напрямлені в сторону, протилежну показаній на рис. С2.3.

Визначимо рівнодійні зусилля в шарнірі С і в опорі В:

кН,

кН.

Відповідь:  кН·м;  кН;  кН;  кН.

Розглянемо один з варіантів використання прикладного математичного пакета серії Mathcad. Для розв’язку задачі скористаємось операторами Given та Find.

1. Задаємо вихідні дані та обнуляємо значення шуканих реакцій. Розмірності сил задано в кН, моменту – в кНм, величина кута  – в рад.

F _1x:=9.96 F_2x:=7.37 Q₁:=9 Q_1x:=5.78 Q_2x:=2.89 M:=8.5

F_1y:=8.36 F_2y:=5.16 Q₂:=4.5 Q_1y:=6.89 Q_2y:=3.45

R_A:=0 M_A:=0 R_Cx:=0 R_Cy:=0 R_Bx:=0 R_By:=0

R_C:=0 R_B:=0

2. Записуємо систему рівнянь рівноваги.

Given

Q₂ + Q₁1.5 + M_A – R_A(2 + 6cos()) = 0

– F_1x + Q_1x + Q_2x + R_Cx = 0

R_A – F_1y – Q_1y – Q_2y + R_Cy = 0

F_2x1.5sin (a)+ F_2y1.5cos(a) – M + R_By1.5×cos(a) + R_Bx×(9.5 – 1.5×cos(a)) = 0

– R_Cx –F_2x + R_Bx = 0

– R_Cy + F_2y + R_By = 0

3. Розв’язок системи рівнянь –

D:=Find(R_A, M_A, R_Cx, R_Cy, R_Bx, R_By)

4. Перевірка правильності визначення опорних реакцій.

Q₂1 + Q₁1.5 + D₀₁  – D₀₀(2 + 6×cos()) + F_2x1.5sin() + F_2y1.5cos() –

– M + D₀₅1.5×cos(a) + D₀₄×(9.5 – 1.5×sin(a)) = – 1.279  10^-13

5. Визначимо рівнодійні реакцій в шарнірі С та в опорі В –

Величини опорних реакцій, отриманих за допомогою Mathcad, збігаються з результатами аналітичного розв’язку.