Контрольное задание к теме №10

1. Дискретная случайная величина х – число мальчиков в семьях с 5 детьми. Предполагая равновероятными рождения мальчика и девочки: а) найдите закон распределения х; б) постройте многоугольник распределения; в) найдите вероятности событий: А – в семье не менее 2, но не более 3 мальчиков; В – не более 3 мальчиков; С – более одного мальчика.

2. С вероятностью попадания при одном выстреле 0,7 охотник стреляет по дичи до первого попадания, но успевает сделать не более 4 выстрелов. Дискретная случайная величина х – число промахов. а) Найдите закон распределения х. б) Постройте многоугольник распределения. в) Найдите вероятности событий: x < 2; x  3; 1 < x  3.

3. 2 стрелка делают по одному выстрелу в одну мишень. Вероятность попадания для первого стрелка при одном выстреле – 0,5, для второго – 0,4. Дискретная случайная величина х –число попаданий в мишень. а) Найдите закон распределения х. б) Постройте многоугольник распределения. в) Найдите вероятность события х  1.

4. В коробке имеются 7 карандашей, из которых 4 красные. Из этой коробки наудачу извлекаются 3 карандаша. а) Найдите закон распределения случайной величины х, равной числу красных карандашей в выборке. б) Постройте многоугольник распределения. в) Найдите вероятность события 0 < x  2.

5. Из 25 контрольных работ, среди которых 5 оценены на «отлично», наугад извлекают 3 работы. Найдите закон распределения дискретной случайной величины х, равной числу оцененных на «отлично» работ среди извлеченных. Чему равна вероятность события x > 0?

6. Дискретная случайная величина х имеет закон распределения:

xi	0	3	4	5	8
pi	0,2	0,1	0,3	p4	0,15

Чему равна вероятность Р₄ = Р (х = 5)? Постройте многоугольник распределения.

7. Имеются 5 ключей, из которых только один подходит к замку. Найдите закон распределения случайной величины х, равной числу проб при открывании замка, если испробованный ключ в последующих опробованиях не участвует.

8. В партии из 10 деталей имеется 8 стандартных. Из этой партии наудачу взято 2 детали. Найдите закон распределения случайной величины, равной числу стандартных деталей в выборке.

9. Дважды брошена игральная кость. Случайная величина х равна разности между числом очков при первом бросании и числом очков при втором бросании. Найдите закон распределения х и вероятность события 2  х  4.

10. Бросается игральная кость до первого появления шестерки. Случайная величина х равна количеству бросаний кости. Найдите закон распределения случайной величины х и вероятность события х  5.

Тема №11 Функция распределения случайной величины

На практике для задания случайных величин общего вида обычно используется функция распределения.

Вероятность того, что случайная величина х примет определенное значение х₀ , выражается через функцию распределения по формуле

р (х = х₀) = F(x₀ +0) – F(x₀). (3)

В частности, если в точке х = х₀ функция F(x) непрерывна, то

р (х = х₀) =0.

Случайная величина х с распределением р(А) называется дискретной, если на числовой прямой существует конечное или счетное множество , такое, что р(,) = 1.

Пусть  = {x₁, x₂,…} и p_i = p({x_i}) = p(x = x_i), i = 1,2,…. Тогда для любого борелевского множества А вероятность р(А) определяется однозначно формулой

. (4)

Положив в этой формуле А = {x_i / x_i < x}, x  R, получим формулу для функции распределения F(x) дискретной случайной величины х:

F(x) = p(x < x) = . (5)

График функции F(x) представляет собой ступенчатую линию. Скачки функции F(x) в точках х = х₁, х₂ …(x₁<x₂<…) равны соответствующим вероятностям р₁, p₂, ….

Пример 1. Найдите функцию распределения

дискретной случайной величины х из примера 1 § 13.

Используя функцию распределения, вычислите

вероятности событий: х < 3, 1  x < 4, 1  x  3.

Р

0 х₁ х₂ х₃ х₄ х

F(x)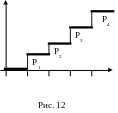

ешение. Используя данные из таблицы,

полученной в § 13, и формулу (5), получим

функцию распределения:

По формуле (1) Р(x < 3) = F(3) = 0,1808; по формуле (2)

р(1  x < 4) = F (4) – F(1) = 0,5904 – 0,0016 = 0,5888;

p (1  x  3) = p ( 1  x <3) + p(x = 3) = F(3) – F(1) + F(3+0) – F(3) =

= F(3+0) – F(1) = 0,5904 – 0,0016 = 0,5888.

Пример 2. Дана функция

Является ли функция F(x) функцией распределения некоторой случайной величины? В случае положительного ответа найдите . Построить график функции F(x).

Решение. Для того чтобы наперед заданная функция F(x) являлась функцией распределения некоторой случайной величины х, необходимо и достаточно выполнение следующих условий (характеристических свойств функции распределения):

1. F (x) – неубывающая функция.

2. , .

3. При любом х  R F(x – 0) = F(x).

Для заданной функции F(x) выполнение

этих условий очевидно. Значит,

F(x) – функция распределения.

Вероятность вычисляем по

формуле (2):

.

График функции F(x) представлен на рисунке 13.

Пример 3. Пусть F₁(x) и F₂(x) – функции распределения случайных величин х₁ и х₂ соответственно, а₁ и а₂ – неотрицательные числа, сумма которых равна 1.

Доказать, что F(x) = a₁F₁(x) + a₂F₂(x) является функцией распределения некоторой случайной величины х.

Решение. 1) Так как F₁(x) и F₂(x) – неубывающие функции и а₁  0, а₂  0, то a₁F₁(x) и a₂F₂(x) - неубывающие, следовательно, их сумма F(x) тоже неубывающая.

2) ;

.

3) При любом х  R F(x - 0) = a₁F₁(x - 0) + a₂F₂(x - 0)= a₁F₁(x) + a₂F₂(x) = F(x).

Пример 4. Дана функция

Является ли F(x) функцией распределения случайной величины?

Решение. Легко заметить, что F(1) = 0,2 > 0,11 = F(1,1). Следовательно, F(x) не является неубывающей, а значит, не является функцией распределения случайной величины. Заметим, что остальные два свойства для данной функции справедливы.