4.3. Забезпечення стабільної роботи автоматів.

На етапі структурного синтезу синхронних цифрових автоматів з пам’яттю однією із головних задач є забезпечення стабільної їх роботи. Поняття стабільності пов’язано із розробкою такої принципової електричної схеми автомата, яка забезпечувала б його функціонування у відповідності з таблицею переходів і виходів. Неправильне функціонування автомата

пов’язане з особливостями фізичної реалізації логічних елементів і елементів пам’яті його схеми, а також різними величинами затримок поширення сигналу в елементах і комбінаційних схемах.

Розглянемо питання забезпечення стабільності роботи автомата детальніше.

Після надходження чергового вхідного сигналу і формування сигналу збудження на входах елементів пам’яті автомат переходить в новий стан. При цьому відбувається формування нових сигналі збудження по ланцюгах зворотних зв’язків (з виходів елементів пам’яті через логічні елементи на входи елементів пам’яті), і автомат переходить в новий стан і т. д. Таким чином, автомат загалом не може зупинитися в якому-небудь певному стані і починає працювати в режимі генератора станів. Для усунення такого ефекту використовують тактування – послідовність спеціальних (зазвичай прямокутних) сигналів, що подаються на входи елементів пам’яті і дозволяють надходження чергових сигналів збудження на входи елементів пам’яті тільки з приходом чергового синхросигналу. При відсутності синхросигналу сигнал збудження не надходить на вхід елемента пам’яті і він не переключається, тобто залишається в якому-небудь стані. Тактуючі сигнали підключають до спеціальних входів елемента пам’яті, які позначаються на рисунках символом і називаються синхровходами.

Однак, введення синхросерії не забезпечує стабільної роботи автомата, якщо не враховувати деякі особливості. При переході автомата із одного стану в інший можливі наступні ситуації:

- якщо черговий синхросигнал на вхід елементів пам’яті автомата надходить раніше, ніж закінчилися перехідні процеси в його комбінаційній схемі збудження і елементах пам’яті після надходження вхідного сигналу, то можливе неправильне формування сигналу збудження на вході одного або кількох елементів пам’яті автомата, тобто автомат може замість правильного переходу здійснити хибний перехід;

- якщо тривалість вхідного сигналу перевищує тривалість переходу автомата в інший стан, то автомат може (при надходженні чергового синхросигналу) проскочити правильний стан і одразу потрапити в наступний стан за рахунок подвійного спрацьовування автомата по одному вхідному сигналу, тобто стан автомата може виявитись нестабільним.

Для забезпечення стабільності автомата потрібно рознести в часі момент подачі інформації на входи його елементів пам’яті і момент знімання інформації з виходів елементів пам’яті. При такому рознесенні формування чергового сигналу збудження будь-якого елемента пам’яті при появі синхросигналу здійснюється тільки за значеннями станів елементів пам’яті в попередній момент часу, а перехідні процеси в елементах пам’яті не впливають на формування сигналу збудження (виходи елементів пам’яті відключені). Звичайно, що період слідування синхросигналів при цьому має вибиратися із врахуванням закінчення перехідних процесів, пов’язаних із затримками поширення вхідного для автомата сигналу логічними елементами комбінаційної схеми збудження.

Розглянемо перехідні процеси, що виникають в комбінаційних схемах збудження цифрового автомата при поширенні вхідного сигналу.

Перехідні процеси в логічних елементах.

Логічним схемам властиве явище затримки спрацьовування. Затримки логічних елементів складаються із затримок їх спрацьовування і затримок поширення сигналів ланцюгами зв’язку між ними. Значну складність врахування затримок становить співвідношення значень затримок самих логічних елементів і затримок в ланцюгах зв’язків. Якщо затримки логічних елементів розмірні, то затримки різних трактів схеми можна визначити тільки після розміщення логічних елементів на поверхні плати чи кристала ВІС, тобто коли стануть відомі фактичні довжини зв’язків. Якщо затримки деяких ланцюгів зв’язків не відповідають вимогам, то виникає ітераційний процес переставлення елементів, який може бути досить тривалим.

В цифрових схемах зазвичай використовуються логічні елементи з часом переключання 10 – 20 нс, що приблизно на порядок перевищує затримку поширення сигналів в будь-якому провіднику монтажної плати типового розміру. Паразитна ємність монтажу при використанні типових плат також не настільки велика, щоб суттєво змінити затримку елемента. В такому разі: затримку монтажу в платі і близького між платного монтажу раціонально не враховувати окремо, а включати її в склад затримки логічного елемента; такі технічні етапи проектування, як розміщення елементів і трасировка зв’язків, виконуються теж тільки один раз і не викликають необхідності корегування функціональної схеми.

Надалі будемо вважати, що затримки в ланцюгах зв’язку включені в затримки логічних елементів.

Ситуації, коли затримки в зв’язках перевищують затримки в елементах, виникають при використанні не дуже швидкодіючих елементів і при передачі сигналів між блоками, розміщеними на значній відстані. Але такі ситуації можна окремо вилучити і врахувати затримку в кабелі.

Затримки різних екземплярів елементів якого-небудь певного типу мають технологічний розкид, який зазвичай описують деяким статистичним законом. Крім того, затримки кожного конкретного елемента залежать від: температури; фронту вхідного імпульсу; на скільки (і які) елементів він навантажений; паразитної ємності монтажу; часу роботи з моменту випуску, тощо.

Кожний елемент певної серії має паспорт. В паспортах елементів вплив частини раніше наведених факторів враховується у вигляді графіків, таблиць, залежностей. Однак, найчастіше вплив цих факторів оцінюється за максимумом. При цьому паспортні значення затримок і фронтів наводяться для найгіршого випадку.

Ефективним засобом аналізу перехідних процесів в схемах є часові діаграми. При їх побудові стани невизначеності схеми, тобто такого стану, який розробнику невідомий, зображають одним із двох способів. Розглянемо їх на прикладі елемента І (див. рис. 4. 5).

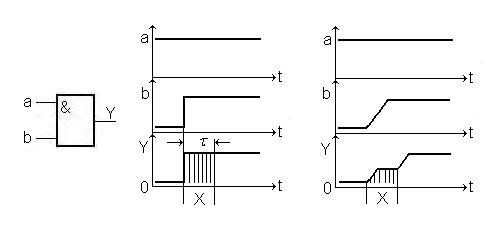
Рис. 4. 5. Часові діаграми логічного елемента І.

Визначення. Рівень виходу логічного елемента впродовж відрізку часу від мінімально можливого до максимально можливого значення затримки, коли фактичний стан виходу елемента розробнику невідомий, називають станом невизначеності і позначають символом „ ”.

Стан „ ”, надходячи на входи інших логічних елементів, може в залежності від типу елемента породжувати на їх виході або визначені стани одиниці чи нуля, або також невизначений стан, позначуваний . Поводження логічного елемента при цьому задається законами троїстої логіки.

; ; ; ; - кон’юнкція

; ; ; - диз’юнкція

; ; ; -

Тут , , - невизначені значення сигналів на входах елементів.

На рис. 4. 5. для елемента І лінії зі стрілками позначають причинно – наслідкові відношення в ланцюжку переключань. Лінія починається на фронті, який безпосередньо викликає переключення розглядуваного елемента, і закінчується стрілкою на фронті вихідного сигналу даного елемента. Зазвичай побудова і аналіз часових діаграм виконуються на ЕОМ за допомогою моделювання.

Гонки. Природа їх виникнення.

В логічних схемах зустрічаються ділянки, де сигнал розгалужується. Два сигнали, що вийшли при цьому, поширюються двома незалежними ланцюжками елементів, а потім обидва сигнали знову зустрічаються на входах одного елемента.

Приклад. Допустимо, є наступна схема, зображена на рис. 4. 6.

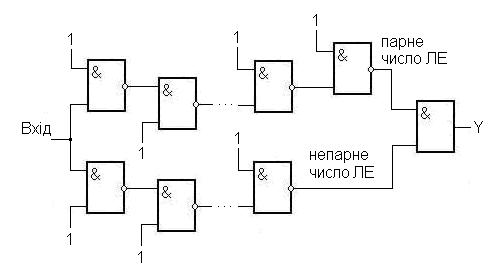
Рис. 4.6. Функціональна комбінаційна схема.

Маємо ланки парного і непарного числа кон’юнкторів. Проаналізуємо роботу даної схеми методами булевої алгебри без врахування затримок. Аналіз показує, що , тобто на виході схеми завжди має бути 0. Зазначимо при цьому, що всі кон’юнктори в схемі прозорі для вхідного сигналу завдяки тому, що всі вони відкриті сигналами одиничного рівня. Сказане можна проілюструвати ідеалізованими часовими діаграмами (див. рис. 4. 7,а).

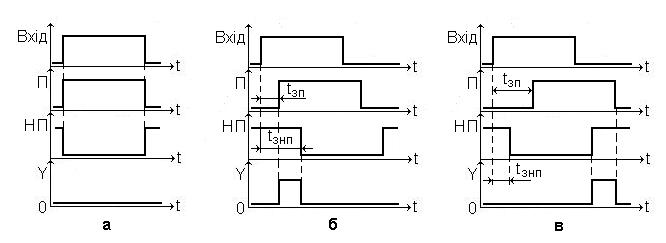
Рис. 4. 7. Часові діаграми роботи КС: а – ідеалізовані;

б − при ; в – при

Однак, реальні елементи мають кінцеву затримку спрацьовування, і якщо позначити затримки в ланках „парна” і „непарна” через і , то в залежності від співвідношення цих величин можемо одержати два процеси: при і . Нехай . Тоді часові діаграми роботи схеми будуть мати вигляд (див. рис 4. 7, б). Як бачимо з часових діаграм, при на виході КС виникає паразитний сигнал – завада. Аналогічним чином можна переконатися, що в реальних умовах завада виникає на виході КС і при (див. Рис. 4. 7, в).

Отже, в реальних умовах при у вихідному сигналі КС появляється завада, не передбачена булевими виразами. При досить великій різниці між і завада буде мати тривалість, набагато більшу ніж час переключання логічного елемента, і амплітуду, рівну амплітуді номінального сигналу. Це вже повноцінний логічний сигнал, на який можуть реагувати наступні елементи. Якщо вихід даної комбінаційної схеми під’єднати до входу тригера автомата з пам’яттю, то завада запам'ятається і буде впливати на наступні процеси в пристрої (зміниться внутрішній стан автомата).

Описане явище називається „гонками” або змаганнями.

Основна проблема полягає в тому, що розробник загалом не знає, в якому тракті затримка виявиться меншою. Це пояснюється тим, що виготовляч елементів гарантує лише максимальний час затримок елемента даного типу і нічого не вказує ні щодо конкретних величин затримок того чи іншого елемента, ні щодо мінімально можливого часу затримки. Спеціальний підбір елементів за затримками в умовах сучасного автоматизованого масового виробництва не допустимий. Перевірка реально одержаного співвідношення затримок також неприйнятна, оскільки дорога. Єдина гарантія для розробника – це ТУ (технічні умови) на елемент, на що і слід розраховувати. Тоді, як же бути в даній ситуації?

Методи боротьби з гонками.

Існують три методи боротьби з гонками: введення тактування; побудова протигоночних схем; врахування мінімального часу затримки.

Найбільш універсальним, ефективним і широко поширеним являється метод тактування. Він полягає в тому, що по всьому цифровому пристрою розводиться єдина система тактуючих (синхронізуючих) сигналів. Широко поширена двотактна або двофазна система синхронізації, в котрій використовуються дві періодичні послідовності синхросигналів і , зміщені в часі (Рис. 4. 8).

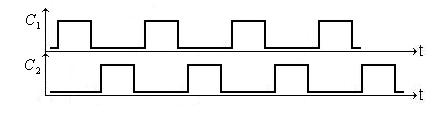
Рис. 4. 8. Двофазна система синхронізації.

Доповнимо розглянутий раніше фрагмент схеми (рис. 4. 6) елементом пам’яті. Одержана схема цифрового автомата (Рис. 4. 9) поділена умовно

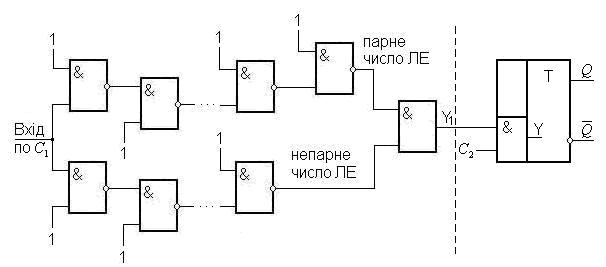
Рис. 4. 9. Функціональна схема цифрового автомата з пам’яттю.

штриховою лінією на дві частини. Ліва частина приймає і обробляє сигнал „Вхід”. Її вихідний сигнал являється вхідним для правої частини автомата, яка запам’ятовує результат на тригері . Допустимо, що сигнал „Вхід” „прив’язаний до синхросерії , тобто подається на вхід одночасно із сигналом . Тоді він буде змінюватися тільки в момент надходження , а в інтервалі між сигналами буде залишатися постійним. Ліва частина даної схеми має паралельні шляхи. В ній існують гонки і можлива поява на виході хибних сигналів.

На вхідний кон’юнктор „ ” правої частини схеми подаються сигнали синхросерії . Обов’язковою умовою являється такий часовий зсув синхросерії відносно синхросерії , який перевищує найдовший інтервал невизначеності, тобто найбільшу затримку із всіх паралельних ланок схеми. Це означає, що сигнал відкриє кон’юнктор „ ” після закінчення всіх перехідних процесів в схемі і пропустить логічно правильне, не спотворене гонкою, усталене значення функції . Зазвичай кон’юнктор „ ” входить в склад тригера, що робить тригер синхронним. Такий тригер переключається тільки за командою синхросигналу і не сприймає інформацію при його відсутності. Кон’юнктор „ ” застосовують і без тригера тоді, коли немає необхідності у запам’ятовуванні вихідного сигналу схеми, а потрібно лише очистити його від завад, викликаних гонками. В такому разі сигнал, що відкриває кон’юнктор „ ”, зазвичай називають не синхросигналом, а стробом, а сам процес відсікання завад – стробуванням.

Система синхронізації є єдиною для всього цифрового пристрою і інтервал між синхросигналами задається на початку розробки. Все, що має знати розробник при такому підході – це максимально можливу затримку найдовшої ланки логічної схеми. Максимальну затримку просто обчислити за паспортними даними використовуваних елементів.

Протигоночні схеми – це схеми, побудовані так, що в них якщо і виникають, то тільки не небезпечні гонки, тобто такі гонки, при яких відсутній ризик появи на виході сигналів, не передбачених логічним виразом. Наприклад, гонка фронту по двох ланках, кожна із яких складається із парного (чи непарного) числа інверторів, і які об’єднуються на виходах елементом АБО. При цьому, хто б не виграв гонку, результат однаково буде вірним, зміниться тільки затримка його одержання. Корисною властивістю протигоночних схем являється їх здатність обробляти дані по мірі їх надходження, тобто асинхронно (без прив’язки до тактуючих сигналів).

Стабільність роботи цифрового автомата може бути забезпечена також при використанні двоярусної пам’яті. При цьому кожний елемент пам’яті дублюється і перепис інформації із нижнього елемента пам’яті у верхній здійснюється при відсутності синхросигналу. Сигнали зворотних зв’язків, що використовуються для формування функцій збудження, і сигнали виходів автомата знімаються з виходів елементів пам’яті верхнього ярусу. При такій організації пам’яті автомата відсутня небезпека формування повторного сигналу збудження за одним і тим же синхросигналом і переходу автомата в новий стан. Це пояснюється тим, що перехід в робочий стан автомата завершується після закінчення дії синхросигналу. Однак використання подвійної пам’яті автомата веде до уповільнення роботи автомата. Якщо зазвичай період синхросигналів вибирається із розрахунку, що сигнал збудження елемента пам’яті встигне пройти найдовшою ланкою логічних елементів і переключить елемент пам’яті, то в цьому разі період потрібно подовжити принаймні на , де − затримка поширення сигналу в логічному елементі ( − на інвертор і − на другий елемент пам’яті).

У випадках, коли із міркувань швидкодії двоярусну пам’ять використовувати не можна, застосовують багатофазну систему тактування вхідних сигналів автомата. Так, наприклад, при двофазній синхронізації і замість одного вхідного сигналу використовуються два різних: і . Таким способом стабільність функціонування автомата забезпечується автоматично.

Отже, проблема гонок в цифровій схемотехніці є надзвичайно серйозною. Більшість помилок у функціональних схемах пов’язана з гонками. Основна причина полягає у обмеженості поля уваги людини. Гонки у розробленій схемі шукаються спеціально.

Останнім часом зростає інтерес ще до одного способу боротьби з гонками – побудови схем, які само синхронізуються. Робочі вузли в таких схемах будуються не протигоночними, а доповнюються спеціальними схемами. Такі схеми виявляють факт закінчення перехідних процесів і виробляють сигнал дозволу для наступних вузлів схеми. Сигнал дозволу являється в певному змісті ніби асинхронним синхросигналом. Даний напрям боротьби з гонками застосовується при побудові ВІС і НВІС.

Перехідні процеси в елементах пам’яті автомата.

Спосіб кодування станів синхронного автомата не впливає на правильність його переходів з одного стану в інший. Однак при неоптимальному кодуванні станів автомата обумовлює появу вихідних сигналів, непередбачених графом автомата. Це пов’язано з розкидом часу переключення окремих тригерів автомата (так званих „гонок“). Наприклад, під час переходу автомата зі стану 10 у стан 01, відбувається переключення двох тригерів. Через те, що один з тригерів може переключитися раніше ніж другий, можливе виникнення проміжних короткочасних станів 00 або 11 (залежно від того, який із тригерів раніше переключається). Ці проміжні стани можуть привести до появи короткочасних помилкових керуючих сигналів.

На рис. 4. 10, а зображений приклад графа автомата, коди станів якого наведені біля вершин графа.

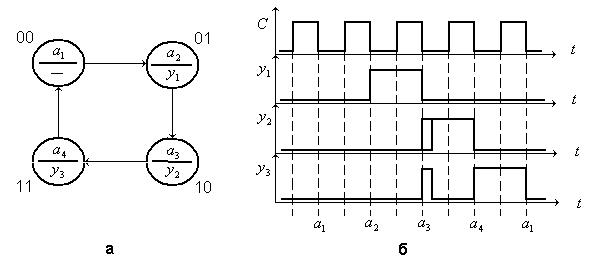
Рис. 4. 10. Приклад виникнення короткочасного помилкового сигналу: а – граф автомата; б – часова діаграма роботи автомата