4. 1. Канонічний метод структурного синтезу автоматів

з пам’яттю

Якщо синтез комбінаційних схем зводиться до реалізації аналітичних виразів булевих функцій за допомогою логічних елементів, то синтез цифрових автоматів з пам’яттю не настільки очевидний.

В загальному випадку задача структурного синтезу автоматів з пам’яттю зводиться до пошуку способів побудови структурних схем складних автоматів на основі композиції деяких елементарних автоматів, тобто пошуку певних способів їх з’єднання між собою. Слід зауважити, що не при всякому виборі системи елементарних автоматів можна побудувати (шляхом їх композиції) будь-який структурний автомат. В разі, коли це можливо, говорять, що задана система елементарних автоматів структурно повна. Однак і на основі структурно повних систем елементарних автоматів ефективно розв’язати задачу структурного синтезу довільного автомата з пам’яттю поки що вдається тільки для структурно повних систем елементарних автоматів деякого спеціального типу.

Розглянемо один із таких методів синтезу, який дозволяє звести задачу структурного синтезу довільного автомата з пам’яттю до задачі синтезу комбінаційних схем. Цей метод називається канонічним методом структурного синтезу автомата з пам’яттю.

Канонічний метод структурного синтезу оперує з елементарними автоматами, що поділяються на два великих класи.

Перший клас складають елементарні автомати з пам’яттю, які називаються елементами пам’яті.

Другий клас складають елементарні комбінаційні автомати – логічні елементи.

Зведення задачі структурного синтезу довільного автомата з пам’яттю до задачі синтезу комбінаційних схем накладає обмеження на тип елементів пам’яті. Результатом роботи методу являються рівняння булевих функцій автомата в канонічній формі подання. Вихідні дані для початку роботи методу – абстрактний автомат з пам’яттю, заданий або графічним способом у вигляді графа, або матричним способом у вигляді таблиць переходів і виходів.

Канонічний метод структурного синтезу умовно можна розділити на наступні етапи:

- кодування;

- вибір елементів пам’яті автомата;

- вибір структурно-повної системи елементів;

- побудова рівнянь булевих функцій виходів і збудження автомата;

- побудова функціональної схеми автомата.

Розглянемо кожний із перелічених етапів детально.

Кодування

Довільний цифровий автомат з пам’яттю на абстрактному рівні подання може бути описаний у вигляді . При переході на структурний рівень подання кожна буква вхідного алфавіту автомата представляється як двійковий вектор або двійковий набір, число компонентів якого дорівнює числу фізично реалізованих вхідних каналів структурного автомата. Одним словом, кожна буква кодується двійковим вектором. Очевидно, мінімальне число фізично реалізованих вхідних каналів в автоматі може бути вирахуване за формулою

,

де - потужність алфавіту входів . Наприклад, якщо , то . Значить кожну букву можна закодувати двійковим вектором, що складається не менше, ніж із двох компонент, наприклад . Кожна буква вихідного алфавіту автомата також подається як двійковий вектор, число компонент котрого дорівнює числу фізично реалізованих вихідних каналів автомата. Аналогічно

мінімальне число компонент двійкового вектора виходів автомата визначається за формулою . Кожна буква алфавіту станів автомата подається двійковим вектором , мінімальне число компонент якого визначається за формулою .

Процес заміни букв алфавітів абстрактного автомата двійковими векторами називається кодуванням і може бути описаний таблицями кодування. Таблиця кодування складається так: у лівій її частині перелічуються всі букви (наприклад, вхідного алфавіту абстрактного автомата), а в правій – двійкові вектори, котрі ставляться у відповідність цим буквам.

Приклад. Абстрактний автомат Мілі заданий суміщеною таблицею переходів і виходів (табл. 4. 5). Кодування букв алфавітів зображено відповідними таблицями кодування (табл. 4. 6; 4. 7; 4.8). При цьому, оскільки , то ; ; .

Таблиця 4. 5 Таблиця 4. 5 Таблиця 4.7

Стани автомата	Вхідні сигнали			Вхідні сигнали	Код вхідних сигналів		Стани	Код станів
					0 1

Таблиця 4. 8 Таблиця 4. 9

Вихідні сигнали	Код вихідних сигналів		Стани автомата	Вхідні сигнали
	00 01 10 11		00 01 10	01/00 01/01 10/00	00/10 00/11 01/01

Зауважимо, що в загальному випадку кожній букві, що кодується, може бути приписаний довільний двійковий вектор, але обов’язково дві різні букви (одного й того ж алфавіту) мають кодуватися різними двійковими векторами.

Якщо замінити у вихідній таблиці переходів і виходів букви на двійкові вектори, то одержимо так звану структурну таблицю переходів і виходів автомата (табл. 4. 9). На одержанні структурної таблиці переходів і виходів, етап кодування закінчується.

Вибір елементів пам’яті автомата.

Заміна таблиці переходів на структурну таблицю переходів призводить до того, що функція автомата переходів стає векторною. Це означає, що аргументами такої функції є всі можливі пари двійкових векторів ( ), а сама функція набуває значення із множини двійкових векторів станів автомата. Згідно із структурною таблицею переходів автомата його векторна функція переходів кожної пари двійкових векторів ( ) ставить у відповідність визначений двійковий вектор , що на абстрактному рівні визначається співвідношенням . Звідси виходить, що структурний автомат має запам’ятовувати двійковий вектор кожного чергового стану автомата, для чого слугують елементи пам’яті.

При канонічному методі структурного синтезу автоматів як елемент пам’яті використовуються елементарні автомати Мура з двома станами, які мають повну систему переходів і виходів.

Повнота системи переходів автомата в загальному випадку означає, що для будь-якої пари станів автомата існує вхідний сигнал, який переводить елементарний автомат із одного стану в інший. Таблиця переходів елементарного автомата з повною системою переходів повинна мати в кожному своєму рядку всі можливі стани.

Повнота системи виходів означає, що різним станам автомата відповідають різні вихідні сигнали. Зазвичай нульовому стану елементарного автомата відповідає нульовий вихідний сигнал, одиничному – одиничний.

Очевидно, що число елементів пам’яті структурного автомата дорівнює числу компонент вектора його станів.

Як елементи пам’яті структурного автомата зазвичай використовуються - тригери; - тригери; - тригери; -тригери, які відповідають вимогам стосовно повноти переходів і виходів. Таблиці їх переходів подані табл. 4. 1 – табл. 4. 4 відповідно.

Таблиця 4. 1 Таблиця 4. 2 Таблиця 4. 3

Стани -тригера	Вхідний сигнал			Стани -тригера	Вхідний сигнал			Стани -тригера	Вхідні сигнали
	0	1			0	1			00	01	10
0 1	0 0	1 1		0 1	0 1	1 0		0 1	0 1	1 1	0 0

Таблиця 4. 4

Стани -тригера	Вхідні сигнали
	00	01	10	11
0 1	0 1	0 0	1 1	1 0

Умовні графічні позначення синхронних тригерів і системи підграфів переходів, що пояснюють спосіб зміни стану тригерів, зображені на рис. 4. 1. Тригери мають тільки два стани: нульовий стан ( і ) та одиничний ( і ). Входи , , , , , називаються інформаційними. Таблиці переходів тригерів складаються тільки для інформаційних входів. Всі інші входи являються допоміжними. Перехід тригерів з одного стану в інший визначається інформаційними сигналами, а момент переходу – перепадом синхросигналу (в даному випадку перепад з 0 в 1). Асинхронні входи тригерів і дозволяють встановлювати початковий стан тригерів. Для - тригера

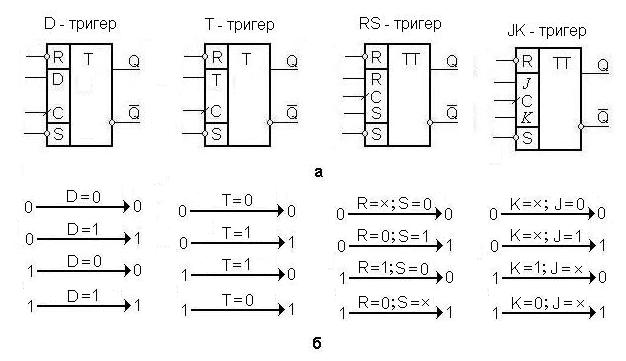
Рис. 4. 1. Синхронні тригери: а – умовні графічні позначення;

б – система під графів переходів

вхідна комбінація заборонена, оскільки може призвести до неоднозначної роботи тригера.

Вибір функціонально-повної системи елементів.

Функціонування структурного автомата в часі припускає керування переключанням кожного елементарного автомата його пам’яті у відповідності із структурною таблицею переходів синтезованого автомата. Останнє здійснюється за допомогою спеціальної комбінаційної схеми, що підключається до інформаційних входів елементарного автомата пам’яті і реалізує перемикальні функції, які керують його переключенням. Такі перемикальні функції називаються функціями збудження елемента пам’яті. Загалом різних функцій збудження стільки, скільки різних інформаційних входів має елементарний автомат пам’яті в структурному автоматі, що синтезується.

Функція збудження будь-якого елемента пам’яті є довільною перемикальною функцією і для її реалізації комбінаційною схемою необхідно використати яку-небудь функціонально-повну систему логічних елементів.

Теоретичним фундаментом канонічного метода структурного синтезу автоматів з пам’яттю являється теорема про структурну повноту.

Теорема про структурну повноту. Всяка система, яка складається із якої-небудь функціонально-повної системи логічних елементів та елементарних автоматів Мура з нетривіальною пам’яттю, котрі мають повну систему переходів і повну систему виходів, є структурно-повною (тобто дозволяє синтезувати довільний цифровий автомат з пам’яттю).

Таким чином, для побудови структурного автомата необхідно крім елементів пам’яті мати комбінаційну схему, яка реалізує перемикальні функції збудження елементів пам’яті автомата, а для вироблення вихідних сигналів структурного автомата – спеціальну комбінаційну схему формування вихідних сигналів автомата.

Побудова рівнянь перемикальних функцій

збудження і виходів автомата

Кодування і вибір системи елементів однозначно визначають комбінаційну схему автомата. Спочатку будується таблиця істинності функцій збудження тригерів і функцій виходів автомата, а потім із побудованої таблиці виписуються рівняння даних перемикальних функцій. Одержані аналітичні записи перемикальних функцій можуть бути мінімізовані будь-яким відомим методом.

Вихідними даними для побудови таблиці істинності функцій збудження тригерів являється структурна таблиця переходів автомата і таблиця переходів елемента пам’яті.

Таблицею істинності перемикальних функцій виходів автомата є його структурна таблиця виходів. Таким чином, рівняння перемикальних функцій виходів автомата не залежить від типу використовуваних елементів пам’яті, однак залежить від їх кількості.

Розглянемо приклад синтезу автомата Мілі. Для організації пам’яті використовуємо, наприклад, - тригери, а для побудови комбінаційних схем – елементи булевого базису.

На основі структурної таблиці переходів і виходів автомата (табл. 4. 9) і таблиці переходів - тригера (табл. 4.3) складаємо таблицю істинності перемикальних функцій збудження тригерів і перемикальних функцій виходів автомата (табл. 4. 10).

Таблиця 4. 10

Код ПС		Код СП		Код вх. сигналів	Вихідні сигнали				Функції збудження тригерів
0	0	0	1	0	1	0	0	0	x	0	0	1
0	1	0	1	0	0	1	0	0	x	0	0	x
1	0	1	0	0	1	0	0	0	0	x	x	0
0	0	0	0	1	0	0	1	0	x	0	x	0
0	1	0	0	1	0	0	0	1	x	0	1	0
1	0	0	1	1	0	1	1	0	1	0	0	1

ПС – початковий стан, СП – стан переходу; знаком „ x “ в таблиці істинності позначені довільні значення аргументів.

На підставі таблиці істинності автомата визначаємо МДНФ функцій збудження тригерів і функцій вихідних сигналів. Аргументами функцій є значення (тобто структурний вхідний сигнал ) та у початковому стані:

; ; ; ;

; ; ; .

Функціональна схема автомата зображена на рис. 4. 4, де УПС −

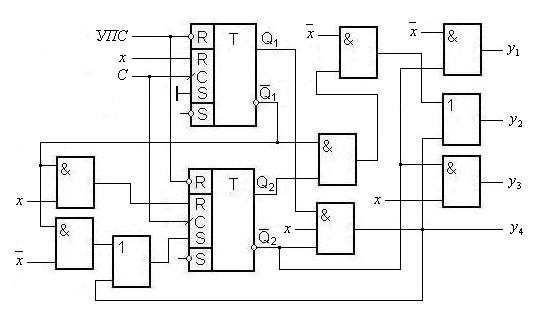
Рис. 4. 4. Функціональна схема автомата

установлення початкового стану, − тактуючі сигнали.

Якщо синтезований автомат є автоматом Мура, то задача побудови рівнянь перемикальних функцій збудження тригерів розв’язується так же. Рівняння ж перемикальних функцій виходів автомата Мура будуються дещо по-іншому. Це пов’язано з тим, що виходи автомата Мура залежать тільки від станів автомата.