1.7 Алгоритм расчета модели системы «пласт – скважина – насос»

1) задание начальных условий:

2) задание управляющих воздействий на весь период переходных процессов: пуск: , останов:

3) в цикле схемы интегрирования:

3.1) расчет давления в забое: ,

расчет напора насоса:

расчет дебита насоса путем численного нахождения корней уравнения (10) через функцию roots(c) , где - вектор-строка коэффициентов уравнения (10).

В обоих случаях из решений уравнений выбираются подходящий корень и назначаются как дебит насоса

3.2) расчет вектора состояния по схеме (14)

Примерные графики переходных процессов системы, полученные в результате моделирования по представленному примеру, изображены на рисунках 3, 4 и 5.

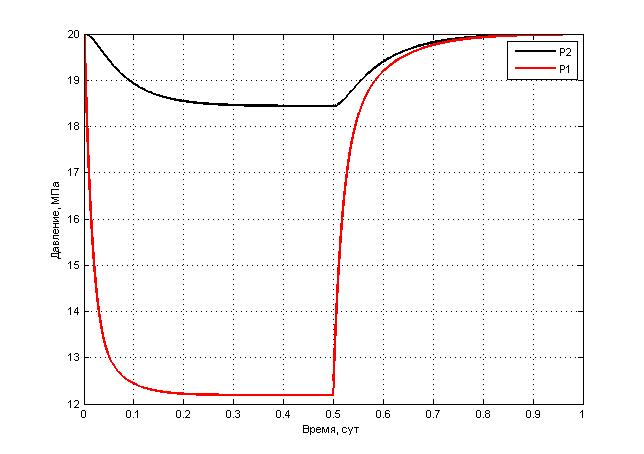
Рис. 3 Переходные процессы давлений в скважине

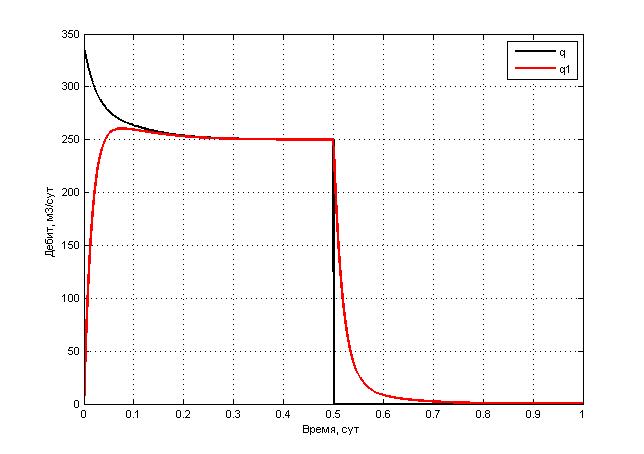
Рис. 4 Переходные процессы расходов жидкости в скважине

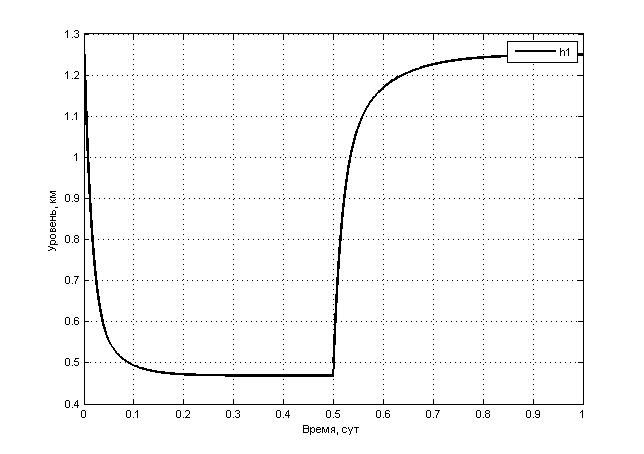
Рис. 5 Переходный процесс уровня жидкости в скважине

2. Схема мнк-идентификации гидродинамики скважинной системы

2.1 Задача гидродинамических исследований скважин (гдис)

К гидродинамическим исследованиям принято относить весь комплекс мероприятий, направленных на измерение ряда параметров скважины (давление, температура, расход, время и др.) на установившихся и неустановившихся режимах ее работы. К основной цели ГДИС относится в–первую очередь - определение параметров призабойной зоны скважины и пласта. Применительно к рассматриваемой модели скважины, эти параметры включают:

а) среднепластовое давление - : среднее давление в зоне пласта (или на контуре питания скважины), принимаемое постоянным.

б) комплексные коэффициенты гидропроводности (продуктивности) скважины - «ПЗ - забой», - «коллектор - ПЗ»

в) параметр гидроупругой характеристики пласта -

2.2 Метод мнк – идентификации гидродинамических параметров пласта

Рассмотрим возможность решения задачи ГДИС с использованием метода МНК – идентификации на базе представленной ранее модели. Для этого необходимо модель скважины (12 - 13) представить в линейно-регрессионном виде. При этом из уравнений системы необходимо исключить те переменные, которые недоступны к прямому измерению.

Примем, что непосредственному измерению, в каждый момент времени доступны следующие переменные: - дебит скважины (насоса), - динамический уровень жидкости в затрубном пространстве. Тогда вывод линейно-регрессионного уравнения будет происходить следующим образом:

а) для исключения переменной не доступной к измерению, выразим ее из второго уравнения системы (12) и подставим в первое уравнение системы:

где - символ оператора дифференцирования.

оставляя в левой части переменную и группируя остаток относительно переменной и ее производной , получим:

(15)

Выражение (15) представляет собой искомое линейно-регрессионное уравнение, и может быть записано в виде:

где - вектор параметров, - вектор регрессионных переменных, формируемый по данным измерений сигналов и .

Оценку вектора параметров получают при помощи схемы МНК – идентификации, при этом решающее правило имеет вид: где , .