1.4 Принципы построения асу и их классификация

. Принципы построения САУ.

САУ несмотря на все разнообразие по конструкции, принципу действия существуют ограничения количество способов их построения. 1) разомкнутая без рефлексная система управления.

ЗУ – задающее устройство; Uз – задающее воздействие; ИУ – исполняющее устройство; U – управляющее воздействие; f – возмущение;Y – выходной сигнал. ЗУ- руководствуясь какими либо внутренними сигналами (часы) измеряет Uз. Через УУ и ИУ это изменение передается на объект управления вызывая изменения управляемой величины Y. Пример: управление стиральных машин. Дост-во: простота конструкции. Недостатки: при наличии возмущающей f выходная величена Y будет отклоняться от определ-го значения, но УУ ничего об этом не знает и никак на это не реагирует. 2) Разомкнутая система управления по возмущениям или принцип Понсле.

Дf – датчик возмущения. Т.к причина отклонения выходной величины Y возмущение f, то его измеряем и в зависимости от его величины, формы формируем управляющее воздействие на объект, чтобы скомпенсировать влияние возмущения на объект. Дост-ва: высокое быстродействие, реагирует на причину. Недостатки: для полной и точной комплектации необходимо иметь точную математическую модель по каналам управления и каналам возмущения. Это дорого и даже эта модель с течением времени

становится не точной. Возмущений может быть несколько, все возмущения измерить дорого и сложно. В результате управляемая величина Y будет отклоняться от заданного значения. 3) замкнутая САУ по отклонению (принцип по отклонению ).

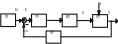
Е=Uз – Uос -> ошибка регулирования управления или отклонения. Здесь величина измеряется и сравнивается с заданным значением. В зависимости от величины и знака отклонения Е управляющее УУ через ИУ воздействует на ОУ стремлясь уменьшить величину отклонения. Дост-ва: универсальность, устройство управления реагирует на любые отклонения. Недостатки: противоречивость самого принципа. Для этого чтобы уменьшить отклонения надо его с начало допустить. 4) Комбинированное САУ.

тр

Действие основного возмущения компенсируется управлением по разомкнутому принципу, а не точность компенсации и влияние неучтенных возмущений устраняется управлением по замкнутому контуру. 5) Адетивное САУ.

СС- система самонастройки.

1.5 Классификация элементов автоматических систем

Классификация систем автоматического управления.

!) По структуре САУ: а) разомкнутые, б) замкнутые, в) комбинированные. 2) По сложности структуры: а)одноконтурные (одна цепь ООС); б) многоконтурные; в) одномерные (если управл. одной переменной); г) многомерная; д) каскадное САУ; е) многоуровневые; ж) иерархические. 3) По цепям управления: а) Uз=const, система автоматической стабилизации; б) Uз=var переменная величина, но измеряется по заранее замкнутой системе т.е программное САУ; в) Uз = var но характер его изменения неизвестен т.е следящее САУ. 4) По виду математического описания: I. а) линейные системы, б) нелинейные

системы. II. а) стационарные если коэфф-ты урав-ий постоянные величины, б) нестационарные системы если коэфф-ты урав-ий динамики системы яв-ся функциями времени. III. а) система сосредоточенными параметрами если описыв. обыкнов. диф. уравнениями, б) система с распределенными параметрами если описыв. диф. урав-ми в частных производных. IV. а) детерминированные системы, б) стохастические если коэфф. уравн-я яв-ся случайными фун-ми. 5) По закону управления: I. Системы с типовыми линейными и не линейными регуляторами: пропорциональный, ПИ, ПИД, ПД, РП, РС; II. оптимальные системы это когда мы стремимся достичь min или max некоторого показателя, III. Адаптивные, самонастраивающиеся системы, в этом случае подстраивается к изменяющимся параметрам окружающей среды, IV. Экстремальные – когда система управления ищет экстремум на характеристиках управления, V. Сомообуч. и самоорганизующие системы. 6) По виду действующих в системе сигналов: I. аналоговые, непрерывные системы, сигналы яв-ся непрерывными ф-ми, II. дискретные сигналы в системе квантованы по уровню, III. импульсные системы, сигналы в системе квантованы по времени, IV. цифровые, когда сигнал квантован и по уровню и по времени, V. смешанные, часть системы яв-ся аналоговой, часть непрерывной, а часть дискретной. Схемы:

T – период квантования.