9 Пример рассчета задания
Дана схема сложной линейной цепи постоянного тока (рис. 9.1) со следующими параметрами:
-
= 15 В,
= 3 Ом,
= 4 Ом,
= 10 Ом,
= 10 В,
= 1 Ом,
= 7 Ом,
= 8 Ом.
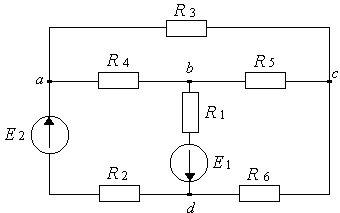
Рисунок 9.1
Выполним
расчет токов
,…
в данной
схеме последовательно всеми предлагаемыми
методами расчета сложных цепей, а также
расчет токов в активных ветвях, а также
токи
,
методом эквивалентного генератора с
погрешностью не более
.
9.1 Метод непосредственного применения законов Кирхгофа
9.1.1. Определим количество ветвей, узлов и независимых контуров в схеме (рис. 9.2):
,
,
9.1.2.
Произвольно выбираем и указываем на
схеме (рис 9.2) направления токов
в ветвях
9.1.3.
Составляем
уравнений
в соответствии с I
законом Кирхгофа:
узел
:
узел
:
узел
:
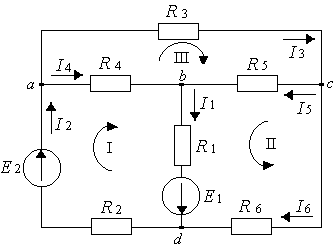
Рисунок 9.2
9.1.4.
Выбираем следующие
независимых
контура (I
контур –aвd,
II
контур – bcd,
III
контур – abc)
и принимаем указанное на схеме (рис.
9.2) направление обхода этих контуров: I
и III
контуры – по стрелке часов, II
контур – против стрелки часов.
9.1.5. Составляем для указанных независимых контуров уравнения в соответствии со II-м законом Кирхгофа:
контур
I:
,
контур
II:
контур
III:
9.1.6.
Получаем следующую систему из
линейных уравнений:
9.1.7. Для решения полученной системы линейных уравнений методом Гаусса приведем ее к канонической векторно-матричной форме:
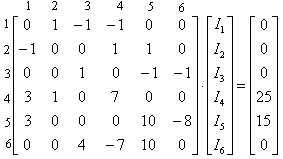
9.1.8. Решение полученной системы с помощью программы “Расчет сложной цепи постоянного тока” дает результат: значения токов
А,
А,
А,
А,
А,
А.
9.1.9. Проверка выполнения баланса отдаваемой и потребляемой мощностей:
;
Вт
=
Вт.
9.1.10. Так как в этом случае все токи имеют знак “+”, нет необходимости изменять их первоначально принятое направление.
9.1.11. Проведем дополнительно контроль решения, проверив выполнение II закона Кирхгофа во внешнем контуре acd:
,
3,0904·1 + 1,1642·4 + 0,2816·8 = 10,0005 ≈10.
9.2 Метод контурных токов
9.2.1.
В качестве
независимых
контуров выбирают следующие контуры
(рис. 9.3): I
контур – abd,
II
контур – bcd,
III
контур – abc.
9.2.2.
Принимаем,
что в каждом из указанных контуров
контурные токи
,
,
протекают по стрелке часов, как это
показано на рис. 9.3.
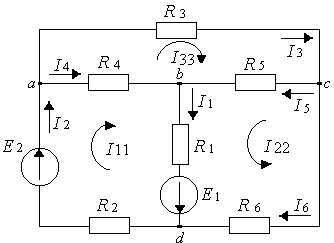
Рисунок 9.3
9.2.3. Вычисляем значения собственных сопротивлений контуров:
Ом,
Ом,
Ом.
9.2.4. Вычисляем значения взаимных сопротивлений контуров:
Ом,
Ом,
Ом.
9.2.5. Вычисляем значения контурных ЭДС:
В,
В,
В.
9.2.6.
Составляем
систему из
линейных уравнений относительно
контурных токов
,
,
:
9.2.7. Решим данную систему с помощью формулы Крамера:
- - ± + +
= 4851 – 210 – 210 – 1029 – 1100 – 189 = 2113,
- - ± + +
= 11025 – 1050 – 2500 – 945 = 6530,
- - ± + +
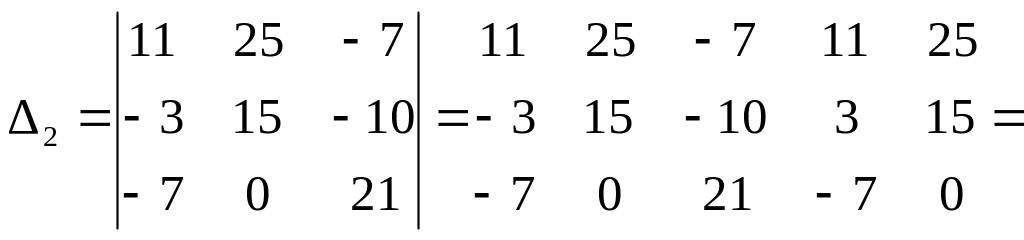
= – 3465 + 1750 +735 + 1575 = 595,
- - ± + +
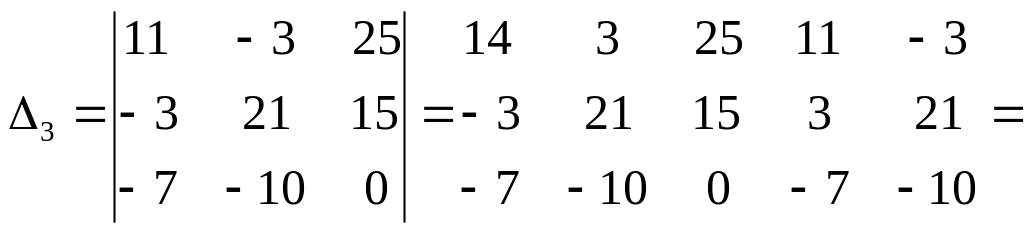
= – 315 + 750 + 3675 – 1650 = 2460.
9.2.8. Решение данной системы имеет вид:
А,
А,
А.
9.2.9. Вычисляем значения токов в ветвях схемы (рис. 9.4):
А,
А,
А,
А,
А,
А.
9.2.10. Укажем на схеме (рис. 9.4) полученные направления токов в ветвях:
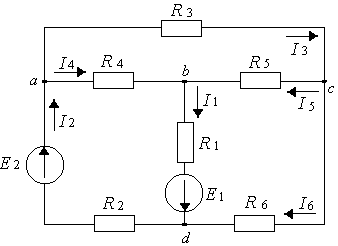
Рисунок 9.4