2.4. Послідовне коло змінного струму

Р озглянемо тепер послідовне з’єднання активного опору, індуктивності та ємності у колі змінного струму. Сила струму в даному колі на всіх ділянках однакова і змінюється за законом (1). У цьому законі ( ) необхідно знайти амплітудне значення сили струму . Також треба знайти сумарне падіння напруги на всіх послідовно з’єднаних елементах кола. Складність цієї задачі полягає в тому, що фаза коливань напруги на різних елементах буде різною. Таким чином, треба додати коливання з однаковими частотами але різними фазами. Для цього скористаємось відомим з теорії коливань методом векторного додавання амплітуд.

Н апруги на окремих ділянках кола з урахуванням їхніх фаз показані на векторній діаграмі, рис. 4. Пояснимо цей рисунок.

Нехай амплітудне значення струму відкладено вздовж горизонтальної осі. Коливання напруги на індуктивності буде випереджувати коливання струму на (або на 90⁰). Тоді вектор , який відповідає амплітудному значенню напруги на індуктивності, буде перпендикулярним до вектора і направленим вгору.

Коливання напруги на ємності будуть відставати від коливань струму на . Тоді вектор (амплітудного значення напруги на ємності) буде перпендикулярним до вектора і направленим вниз.

Коливання напруги на активному опорі будуть відбуватися в тій самій фазі, що і коливання струму. Тоді вектор , який відповідає амплітудному значенню напруги на активному опорі, буде направлений праворуч, паралельно напрямку .

Отже, амплітуда сумарної напруги дорівнює векторній сумі амплітуд напруг на окремих ділянках: . Довжину вектора можна знайти за теоремою Піфагора: буде гіпотенузою трикутника з катетами та . Вона дорівнює , або враховуючи співвідношення (4), (6) та можна записати

.

За другим правилом Кірхгофа, сума амплітуд напруг на окремих елементах кола повинна дорівнювати амплітуді зовнішньої ЕРС, . Тоді можна записати:

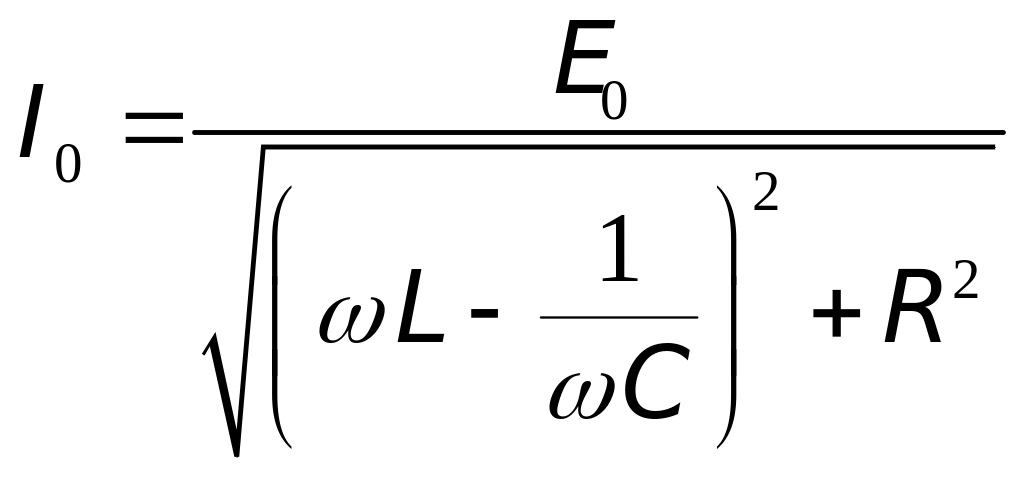(7)

Вираз (7) називають законом Ома для послідовного кола змінного струму. Тут величина

(8)

називається повним опором кола змінного струму або імпедансом. Повний опір складається з активного R і реактивного опорів.

3.Експериментальна частина

3.1. Прилади та устаткування: джерело змінного струму, вольтметр, міліамперметр, реостат, котушка індуктивності, конденсатор.

3.2. Мета роботи:

1. Визначення індуктивності котушки та ємності конденсатора.

2. Визначення повного опору R-L-C кола.

3. Порівняння експериментально знайденого повного опору кола з теоретично обчисленим.

3.3. Порядок проведення вимірювань

3.3.1.Визначення індуктивності котушки.

З беріть електричну схему (рис. 5), яка складається з джерела змінного струму, реостата Р, котушки індуктивності L , міліамперметра mA і вольтметра V.

Котушка індуктивності має активний опір R (опір дроту, з якого вона виготовлена). Тому закон Ома для цього кола (з індуктивним та омічним опорами але без конденсатора) має вигляд: 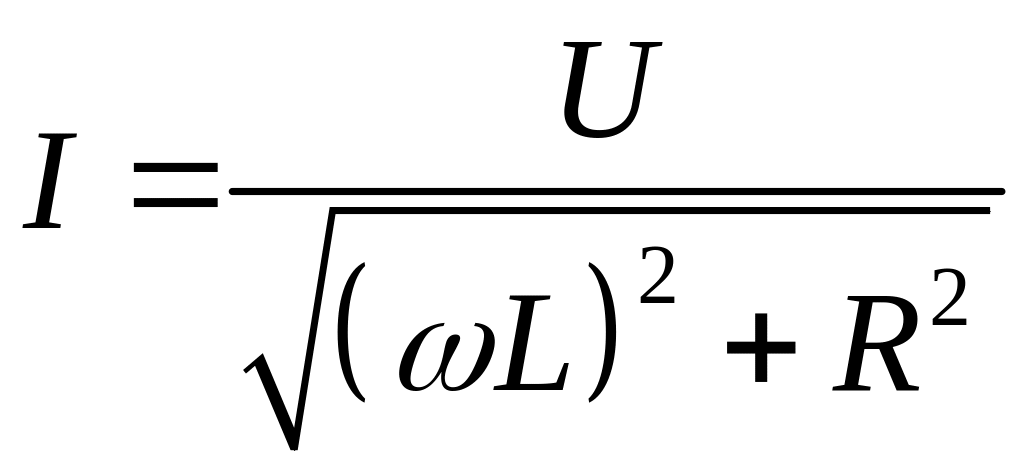. Звідси індуктивність котушки дорівнює

(9)

Після перевірки зібраної електричної схеми викладачем, встановіть за допомогою реостата задане значення сили струму I та визначте відповідну йому напругу U. Вимірювання проведіть для п’яти різних значень сил струмів. Результати вимірювань занесіть в таблицю1.

Таблиця 1.

№ п/п	I, A	U, B	U/I, Oм	Δ(U/I)	[Δ(U/I)]2	R=… Oм
1
. . .
5
Ср.

Знайшовши середнє значення (U/I)_CP , (9) індуктивність котушки.

Похибку індуктивності знайдіть за формулою:

. (10)

Остаточний результат запишіть у вигляді:

3.3.2.Визначення ємності конденсатора.

З беріть електричну схему (рис.6) – в ній замість котушки індуктивності вмикають конденсатор С.

Якщо знехтувати активним опором з’єднувальних провідників, то для цього кола закон Ома прийме вигляд . Звідси

(11)

Для п’яти значень сил струмів I визначте відповідні їм напруги U. Результати вимірювань занесіть в таблицю 2.

Таблиця 2.

№ п/п	I, A	U, B	RC=U/I, Ом	Δ RC, Ом	(Δ RC)2, Ом2
1
. . . .
5

Обчисліть середнє значення ємнісного опору і за формулою (11) – ємність конденсатора.

Визначте середньоквадратичну похибку ємності конденсатора:

. (12)

Остаточний результат запишіть у вигляді:

.

3.3.3. Визначення повного опору R-L-C кола.

Зберіть електричну схему (конденсатор і котушка з’єднані послідовно – рис. 7).

Для заданих п’яти значень сили струму I виміряйте відповідні значення напруги U.

Результати занесіть в таблицю 3.

Таблиця 3.

№	I, A	U, B	Z=U/I, Ом	ΔZ, Ом	(ΔZ)2, Ом2
1
…
5

Обчисліть середнє значення повного опору R-L-C кола.

Знайдіть середньоквадратичну похибку повного опору за формулою

. (13)

Остаточний результат запишіть у виді:

Теоретичне значення повного опору Z_ТЕОР обчисліть за формулою (14), аналогічній виразу (8):

(14)

Порівнюючи Z_ТЕОР і Z_ЕКСП, переконайтесь у справедливості закону Ома для змінного струму.