Завдання для самоперевірки і рівень

1. Обчисліть: –11 · 7.

а) 77; б) –74; в) –77; г) –87.

2. Обчисліть: –12 · (–6).

а) 72; б) –72; в) 62; г) –62.

3. Обчисліть: –45 : (–15).

а) –3; б) 5; в) 2,5; г) 3.

4. Зведіть подібні доданки: 17a + 5a – 10a + 3.

а) 12a + 3; б) 12 + 3; в) 15; г) 2a + 3.

5. Розв’яжіть рівняння: 5x – 3 = 2x.

а)  ; б) 1; в) –1; г)  .

6. Які координати має точка А?

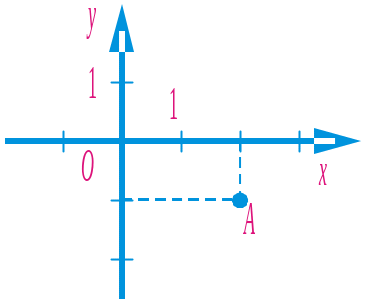
а) (1; 2); б) (–1; –2); в) (2; –1); г) (–1; 2).

Іі рівень

7. Обчисліть:

а) 2,8  15; б) 5  (–1,6);  в) 9 : (–1,5). 

8. Спростіть вираз:

а) –(a + 2) + 2(4  3a); б) 4(2,5  2x) + 2(1,8x + 1).

9. Розв’яжіть рівняння:

а) 2х – 3 = 5 – 3х; б) 4(3,5 + 3х) = 3 + 10х.

Ііі рівень

10. Знайдіть значення виразу:

а) 4,8 : (2,6 + 3,4) + 0,8; б)  + 7,5.

11. Розв’яжіть рівняння:

а) 2,9y  4(1,2  y) = 5,4(y + 2); б) х –   =   + х.

12. У трьох бідонах є 92 л молока, до того ж, у другому бідоні молока удвічі більше, а у третьому  на 4 л менше, ніж у першому. Скільки молока в кожному бідоні?

IV рівень

13. Знайдіть значення виразу (2a  8b + 3)  (–2)  5(–a + 1,8b  1,4), якщо а = 5; b = 1.

14. Шлях між двома містами автомобіль подолав за 1,5 год, а мотоцикліст  за 2 год. Знайдіть відстань між містами, якщо швидкість мотоцикліста на 18 км/год менша від швидкості автомобіля.

15. У першому сховищі є 120 кг яблук, а в другому — 90 кг яблук. Щогодини з першого сховища беруть по 15 кг яблук, а з другого — по 5 кг яблук. Через скільки годин у першому сховищі залишиться яблук удвічі менше, ніж у другому?

ЗАвдання за курс математики 6 класу

Обчисліть:

1389. а) б)

в) ; г) ;

д) : е)  8;

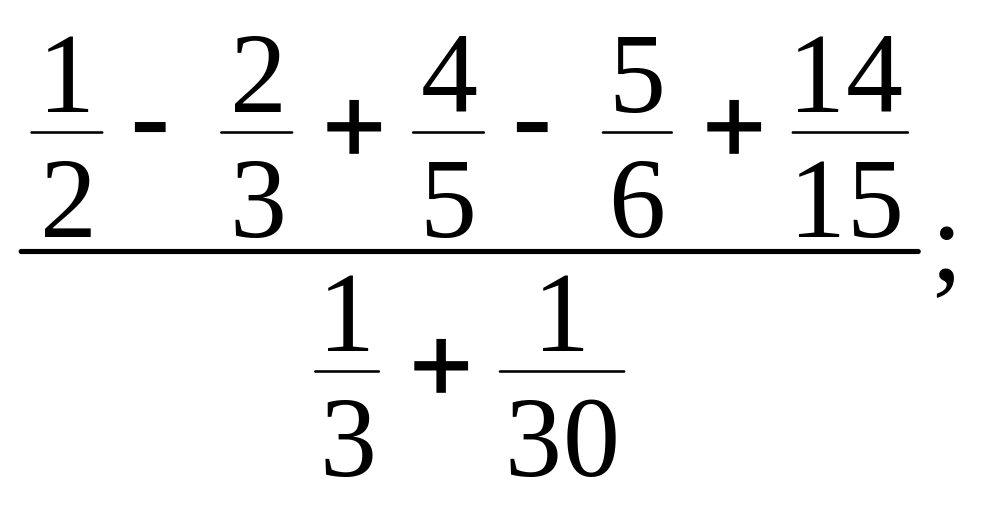є) ж)

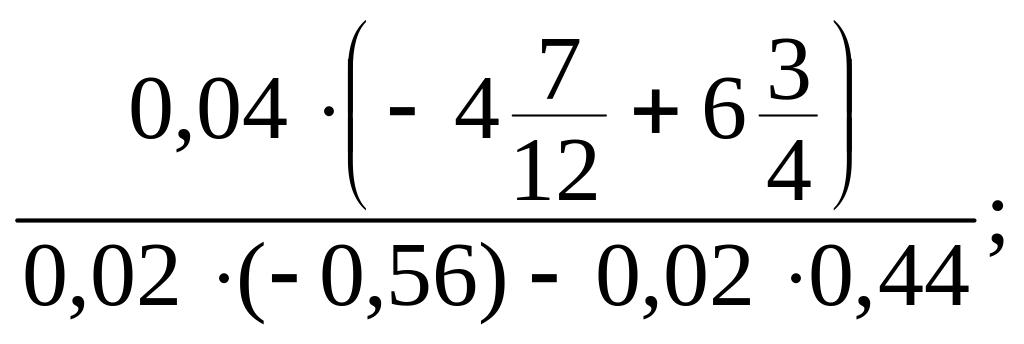
з)

и) 2 ·  + (9,7  1,6) : (0,9).

1390. Порівняйте значення виразів:

а) (4,5²  19,25)³  1,7 і (1,1²  1,3²) : 0,2;

б) (0,1)²  (6,5²  43,245) і (2,5  3)³  (2)³ – 1,99.

1391. Знайдіть пропущені числа:

а) 

б)

1392. Cпростіть вираз:

а) 2(4a  5)  (2  3a); б) 3(5  7x) + 4(x  7);

в) 1,5(2  0,2a) + 3(a + 1); г) 2(1  2a + 7b) – (4a  8b + 1);

д)  (0,5x  1,1)   ; е) (0,25x + 0,3y)  3(0,7x  0,3y).

Розв’яжіть рівняння:

1393. а) 3х  (х + 17) = 21; б) 10  2(7  х) = 8;

в) 4  2(n + 7) = 2n  2(n + 3); г) 5(y + 4) + 3y = 2(3y  4);

д) 2,4х  7,6 = –8(1,2х + 5); е) 2(х  0,8) = 0,8(х  0,8);

є) х  7 + 5(3,6 – 2(x – 3)) = 1; ж) 10(х  1,02) – 2(х  1,2) = 4х;

з) и)

1394. а) 2х + 4,7 = 6,5; б) 6х – 3,2 = 15; в) 2х  (9 – 3х) = 5.

1395. Із чисел 1, 2, 18, 41, 69, 83, 102 випишіть спочатку прості числа, а потім складені. Розкладіть складені числа на прості множники.

1396. Знайдіть НСД і НСК чисел:

а) 20 і 28; б) 35 і 129; в) 48, 64 і 72.

1397. Знайдіть усі дільники числа 72.

1398. Поставте замість зірочок такі цифри, щоб число:

а) 8 ділилось на 9 і на 10; б) 254 ділилось на 3 і на 10;

в) 47 ділилось на 2 і на 3; г) 85 ділилось на 3 і на 5.

1399. Доведіть, що число 249 · 349³ – 117 · 217³ ділиться на 10.

1400. Заповніть порожні кружечки на рисунку 84, знайшовши дроби або від­сотки від числа 80.

1401. Заповніть порожні кружечки на рисунку 85, якщо дріб або відсоток від шуканих чисел дорівнює 12.

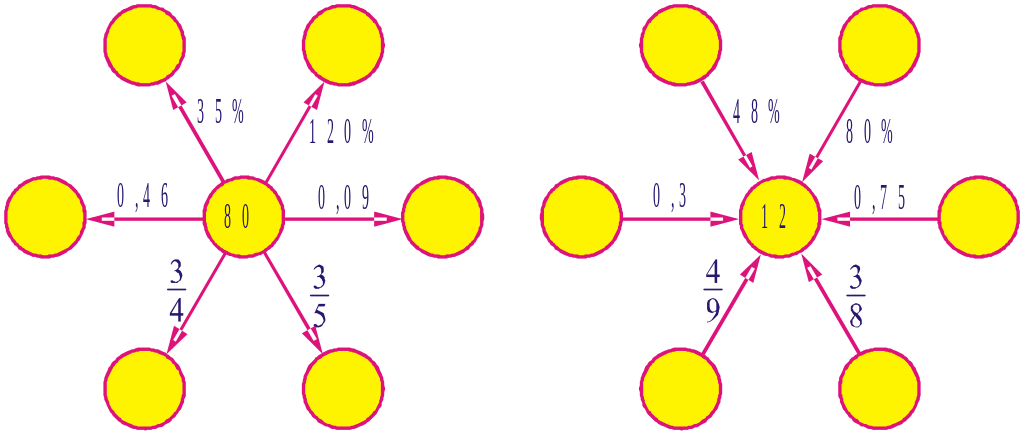Рис. 84     Рис. 85

1402. Чисельник звичайного дробу становить 60% від знаменника. Знайдіть цей дріб, якщо: а) його знаменник дорівнює 5; б) його чисельник дорівнює 9.

1403. Книжка має 160 сторінок. За перший день учень прочитав 15% кіль­кості сторінок книжки, а за другий  в 1,5 разу більше, ніж за перший. Скільки сторінок залишилося прочитати учневі?

1404. Поле площею 18 а засадили картоплею й овочевими культурами, до того ж під картоплю відвели площу на 50% більшу, ніж під овочеві культури. Скільки арів поля відвели під овочеві культури?

1405. Долаючи шлях від міста А до міста В завдовжки 209 км, автобус за першу годину проїхав усього шляху, а за другу — 50% решти шляху. Скільки кілометрів проїхав автобус за ці 2 год?

1406. Ательє закупило тканини трьох видів. Шовк становить усієї тканини, сукно  90% від кількості шовку, а решта  ситець. Яку частину всієї тканини становить ситець? Скільки всього мет­рів тканини було куплено, якщо ситцю купили 165 м?

1407. У школі є 3 шостих класи. У 6–А класі навчається 30% усіх шестикласників, у 6–Б  в 1,2 разу більше, ніж у 6–А. Скільки відсотків усіх шестикласників навчається в 6–В класі? Скільки всього учнів навчається в шостих класах, якщо в 6–В класі є 34 учні?

1408. Один екскаватор може викопати траншею за 8 год, а інший  за 12 год. За який час викопають траншею обидва екскаватори, працюючи разом?

1409. Два муляри можуть викласти стіну за 12 год. За який час може викласти цю стіну перший муляр, якщо другий може це зробити за 20 год?

1410. Перший робітник може виготовити замовлену партію деталей за 6 год, а другий цю ж партію  за 8 год. Спочатку протягом 2 год робітники працювали над замовленням разом, а потім другий робітник закінчував роботу сам. Скільки часу працював над замовленням другий робітник самотужки?

1411. Через першу трубу можна випустити всю воду з басейна за 8 год, а через другу  за 12 год. До обіду з басейна випустили 330 м3 води. Після обіду протягом 1 год випускали воду лише через першу трубу, а потім відкрили ще й другу і за 2 год випустили всю воду. Скільки води було в басейні спочатку?

1412*. Із двох пунктів виїхали одночасно назустріч один одному два автомобілі, і через 1 год 30 хв відстань між ними дорівнювала 30 км. Перший автомобіль може проїхати всю відстань між цими пунктами за 4 год, а другий  за 3 год. Знайдіть швидкість кожного автомобіля.

1413. Із 6 га поля зібрали 87 ц гречки. Скільки гречки зібрали з 34 га поля за такої ж урожайності?

1414. 2,5 кг сплаву олова, міді й цинку містить 800 г олова і 900 г міді. Скільки олова і скільки цинку є у 3,5 кг такого сплаву?

1415. Знайдіть імовірність того, що при підкиданні грального кубика випаде парне число, більше від 2.

1416. В урні є 20 однакових за розміром кульок — 15 білих і 5 чорних. Кульки перемішали. Знайдіть імовірність того, що навмання вийнята кулька буде білою.

1417. З пункту А о 8 год виїхав автобус, а о 9 год услід за ним виїхав легковий автомобіль, швидкість якого на 20 км/год більша від швидкості автобуса. Автобус, рухаючись без зупинок, прибув до пункту В о 14 год, а легковий автомобіль  о 13 год 30 хв.

а) Знайдіть швидкості автомобіля й автобуса.

б) О котрій годині легковий автомобіль наздогнав автобус?

в) На якій відстані від пункту А відбулась їх зустріч?

1418. Відстань між пристанями А і В дорівнює 40 км. Від А до В за течією річки рухається моторний човен, швидкість якого у стоячій воді дорівнює 18 км/год, а від В до А  інший моторний човен, швидкість якого у стоячій воді дорівнює 16 км/год. Коли вони зустрілися, то виявилось, що перший човен ішов 1 год, а другий  1,5 год. Знайдіть швидкість течії річки.

1419. Катер пройшов шлях між двома пристанями, рухаючись за течією річки, за 4,5 год. На зворотний шлях він затратив 6,5 год. Швидкість течії річки дорівнює 4 км/год. Знайдіть відстань між пристанями.

1420*. У двох мішках було 155 кг борошна. Коли з першого мішка пересипали у другий 20 кг, то в першому залишилося тієї кількості, що стало у другому. Скільки борошна було в кожному мішку спочатку?

1421. Сплав міді та цинку, загальна маса якого дорівнює 2 кг, містить 75% міді. Скільки цинку потрібно додати до цього сплаву, щоб одержати новий сплав, який містить 60% міді?

1422. У 10%-й розчин солі додали 100 г солі й одержали 15%-й розчин. Знайдіть масу початкового розчину.

1423. За альбом, 2 лінійки і циркуль заплатили 2 грн. 60 коп. Альбом утричі, а циркуль в 1,5 разу дорожчі від лінійки. Знайдіть ціни альбому, лінійки і циркуля.

1424. На координатній прямій позначте точку D(3) і таку точку С, щоб довжина відрізка CD дорівнювала 2,5 одиниць. Визначте координату точки С. Скільки може бути таких точок?

1425. Знайдіть площі заштрихованих фігур, зображених на рисунку 86, якщо сторони квадратів дорівнюють по 10 см.

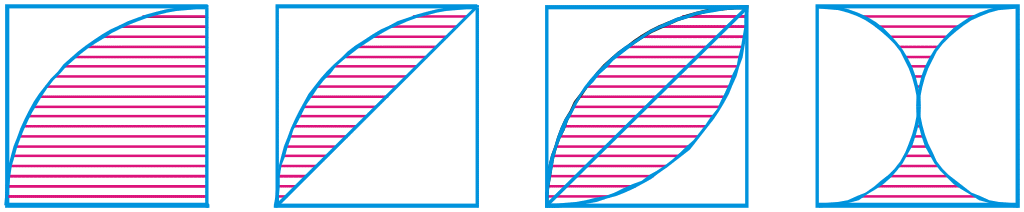Рис. 86