4. Прості й складені числа

Візьмемо кілька натуральних чисел і знайдемо усі їх дільники.

Числа	Дільники	Кількість дільників
1 2 3 4 12 17 21 30	1 1; 2 1; 3 1; 2; 4 1; 2; 3; 4; 6; 12 1; 17 1; 3; 7; 21 1; 2; 3; 5; 6; 10; 15; 30	1 2 2 3 6 2 4 8

Бачимо, що числа мають різну кількість дільників.

Число 1 має найменше дільників — лише один. Числа 2, 3, 17 мають по два дільники: 1 і самого себе. Числа 4, 12, 21 і 30 мають більше, ніж два дільники.

Натуральне число називають простим, якщо воно має тільки два різні дільники: одиницю і саме це число. Число, яке має більше, ніж два дільники, називають складеним.

Отже, числа 2, 3, 17 — прості, а числа 4, 12, 21, 30 — складені. Число 1 не належить ні до простих, ні до складених.

Якщо число має дільник, відмінний від 1 і самого себе, то це число має більше, ніж два дільники, і тому воно є складеним. Число 12 475 — складене, бо має дільником, наприклад, число 5.

Найменшим простим числом є число 2. Найбільшого простого числа не існує. Усі прості числа, крім числа 2, є непарними.

Таблиця простих чисел, що не перевищують 997, вміщена на форзаці підручника.

Усно

84. Чи правильно, що:

а) 31 — просте число; б) 51 — просте число;   

в) 1 — просте число; г) 36 182 — складене число?

85. Доведіть, що числа 175 410, 368 136, 195 435, 111 111, 909 909 є складеними.

86. Чи є значення виразів 112 + 3148, 103  11 та 14 + 3 складеними числами?

87. Чи правильне твердження:

а) кожне парне число є складеним;

б) добуток двох простих чисел є складеним числом?

Рівень А

Скільки дільників мають числа? Випишіть спочатку прості числа, а потім складені:

88. 26; 41; 63; 72; 82; 91.

14; 33; 37; 40; 43; 65.

Доведіть, що числа є складеними:

90. 541 701; 5929; 14 641.

341 105; 43 681; 117 649.

Запишіть замість зірочки таку цифру, щоб утворилося складене число:

92. а) 317; б) 123; в) 5177.

а) 741; б) 418; в) 1896.

Рівень Б

94. Чи можна записати просте трицифрове число, використавши лише один раз кожну із цифр:

а) 2, 6, 8; б) 0, 0, 7; в) 1, 2, 3?

Простим чи складеним є число, записане за допомогою:

95. а) 11 двійок; б) 9 одиниць; в) усіх 10 цифр?

а) 7 п’ятірок; б) 7 трійок; в) 6 одиниць?

97. Чи правильне твердження:

а) добуток будь-яких двох натуральних чисел є складеним числом;

б) якщо натуральне число n ділиться на 3, то n — складене число;

в) якщо натуральне число n ділиться на 4, то n — складене число?

98*. Щоб перевірити, буде число 323 простим чи складеним, Миколка почав послідовно перевіряти, чи будуть числа 2, 3, 4, 5, 6, ... дільниками числа 323. Однак встановивши, що число 3 не є дільником числа 323, Миколка відразу міг би сказати, що деякі наступні числа також не є дільниками числа 323. Які це числа?

99*. Число n просте, до того ж, n > 2. Чи буде наступне за ним число n + 1 простим?

Здогадайтеся

100. Перемноживши чотири простих послідовних числа, Наталя одержала в результаті число, остання цифра якого дорівнює нулю. Які числа вона перемножила і який результат одержала?

Цікаві розповіді Решето Ератосфена

Історія математики знає імена вчених, які чимало працювали над складанням таблиць простих чисел. Перші такі спроби робилися ще у Стародавній Греції.

Для знаходження простих чисел давньогрецький учений Ератосфен (бл. 276 – бл. 194 р. до н. е.) запропонував певний спосіб. Він виписував усі числа від 1 до якогось числа а. Викреслював число 1, яке не є простим. Підкреслював число 2 і викреслював усі числа, які діляться на 2, тобто числа 4, 6, 8, ... . Наступне незакреслене число 3 є простим. Ератосфен підкреслював це число і викреслював усі числа, які діляться на 3. Підкреслював наступне невикреслене число 5, яке є простим, і т. д. У такий спосіб серед чисел, що не перевищують а, можна «висіяти» всі прості числа.

Якщо «висіяти» всі прості числа, що не перевищують 30, то одержимо:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29 — перші 10 простих чисел.

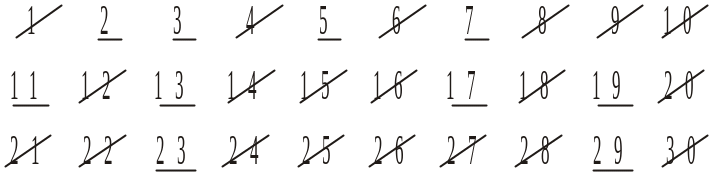
Метод Ератосфена «висіювання» простих чисел називають ще «решетом Ератосфена». Це пов’язано з тим, що давні греки писали на папірусах або табличках, покритих воском, і числа не викреслювали, а виколювали голкою, після чого папірус або табличка нагадували решето.

У 1603 році італійський математик П’єтро Катальді опублікував у Бо­лоньї першу відому нам таблицю простих чисел, менших від 750. Пізніше математики просувалися все далі у глибини натурального ряду чисел, відкриваючи все нові й нові прості числа.

Уже в 1770 році німецький математик Іоан Генріх Ламберт (1728 – 1777) надрукував таблицю найменших дільників усіх чисел, менших від 102 000, які не діляться на 2, 3 і 5. Це була величезна робота. Недаремно ж, закликаючи вчених продовжити складання таблиці, Ламберт гарантував безсмертя тому, хто доведе таблицю дільників до 1 000 000.

У середині XIX століття у пресі з’явилися повідомлення, які здавалися абсолютно неймовірними: до Віденської академії наук надійшов рукопис празького математика Кулика, що містив таблицю дільників чисел, які не діляться 2, 3 і 5, яку вчений розширив до 100 мільйонів.

Редактор таблиць простих чисел Лемер відвідав Відень і пересвідчився, що в бібліотеці академії зберігається сім великих томів рукописних таблиць «Великий канон дільників усіх чисел, які не діляться на 2, 3 і 5, і простих чисел між ними до 100 330 201 Якуба Філіпа Кулика, публічного ординарного професора вищої математики у Празькому університеті».

Якуб Філіп Кулик (1793 – 1863) народився у Львові. Закінчивши місцеву гімназію, він вивчав філософію, право і математику в Львівському університеті, а з 1814 року працював професором математики ліцею. З 1826 року Кулик став професором вищої математики Празького університету. Чимало сил учений віддав розвитку культури, науки й освіти у рідному краї. Він подарував чимало книг галицьким гімназіям та Львівському університету. Кулик є автором багатьох наукових праць, але в історію математики він увійшов як неперевершений обчислювач і укладач математичних таблиць.

Вправи для повторення

101. Автомобіль мав подолати шлях між Львовом i Тернополем за 2 год. Якби він їхав зі швидкістю 60 км/год, то запізнився б на 15 хв. Яка відстань між містами?

102. Мотоцикліст, пробувши в дорозі 1 год 30 хв, приїхав до міста Суми. Їхав він зі швидкістю 40 км/год. На скільки хвилин раніше прибув би до Сум мотоцикліст, якби він їхав зі швидкістю, на 10 км/год більшою?

103. Знайдіть площу квадрата зі стороною 3,6 см. Відповідь запишіть у квадратних дециметрах.

104. Знайдіть об’єм куба з ребром 11 дм. Відповідь запишіть у кубічних метрах.

105. Виконайте дії:

а) 3² – 2³; б) (107 – 972 : 36)²; в) 1,03² – 0,03².