44. Паралельні та перпендикулярні прямі

Ви вже знаєте, що уявлення про площину дає поверхня стола, віконного скла, водойми в тиху погоду (якщо уявити, що всі вони необмежено продовжені в усі боки).

Нехай на столі лежить тонка спиця, а інша стирчить. Розглядатимемо поверхню стола як площину, а спиці — як прямі a та b (рис. 52а). Про прямі a та b кажуть, що вони не лежать в одній площині.

Розглянемо інший випадок. Нехай обидві спиці лежать на столі (рис. 52б). У цьому випадку кажуть, що прямі a та b лежать в одній площині.

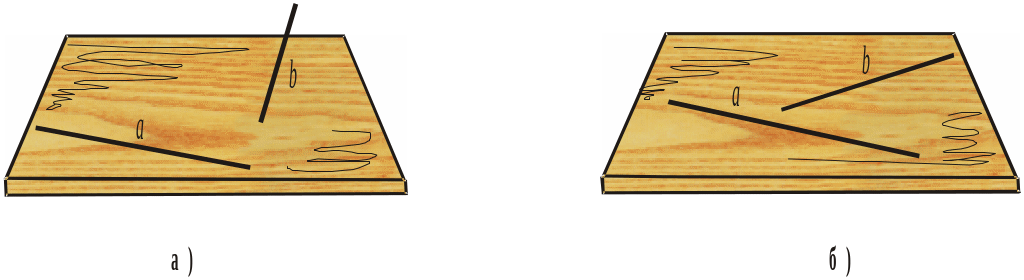Рис. 52

Надалі розглядатимемо прямі, що лежать в одній площині.

Нехай маємо дві прямі АВ і СD (рис. 53). Вони перетинаються, хоча на рисунку не зображено точку їх перетину. Цю точку можна знайти, продовживши зображення прямої СD.

                               Рис. 53              Рис. 54

Прямі a та b (рис. 54) не перетинаються. Такі прямі називають паралельними.

Дві прямі називають паралельними, якщо вони не перетинаються.

Уявлення про паралельні прямі дають рейки залізничної колії на прямолінійній ділянці, слід від санчат при прямолінійному русі, протилежні краї дошки тощо.

Якщо прямі a та b паралельні, то записують: a ^ b; читають: «пряма a паралельна прямій b».

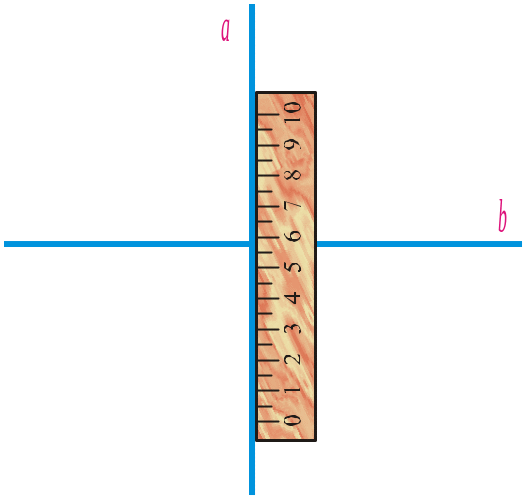
Візьмемо лінійку і косинець. Прикладемо косинець до лінійки однією стороною прямого кута і проведемо пряму a вздовж іншої сторони прямого кута (рис. 55). Пересунемо косинець уздовж лінійки і проведемо ще одну пряму b уздовж цієї сторони прямого кута. Побудовані прямі a та b є паралельними.

Рис. 55

На рисунку 56 зображено прямі a та b, які мають лише одну спільну точку О. Кажуть, що прямі a і b перетинаються.

Якщо при перетині прямих АD і ВС (рис. 57) у точці О промені ОА й ОВ утворюють прямий кут, то прямі AD і BC називаються перпендикулярними.

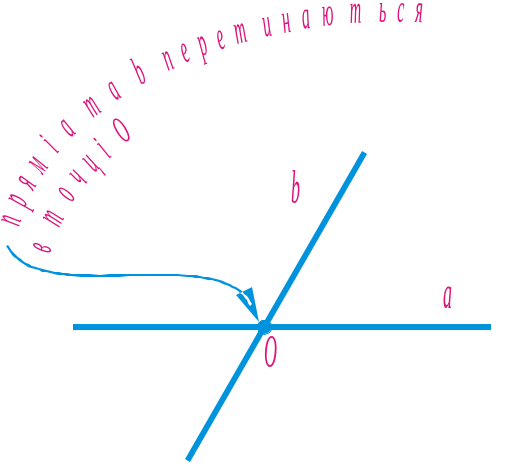
Рис. 56                                      Рис. 57                                 

Дві прямі називають перпендикулярними, якщо вони перетинаються під прямим кутом.

Отже, прямі ВС і АD на рисунку 57 перпендикулярні. Перпендикулярність прямих позначають значком «», записують: ВСАD. Цей запис читають так: «пряма ВС перпендикулярна до прямої АD».

Оскільки кут DОА є розгорнутим (рис. 57), а розгорнутий кут дорівнює 180, то

DОВ = 180 – АОВ = 180 – 90 = 90.

Аналогічно можна встановити, що DОС = СОА = 90. Отже, усі чотири кути, що утворюються при перетині перпендикулярних прямих, є прямими кутами.

Побудувати перпендикулярні прямі можна за допомогою косинця і лінійки. Виконання побудови показане на рисунку 58.

Рис. 58. a та b — перпендикулярні прямі

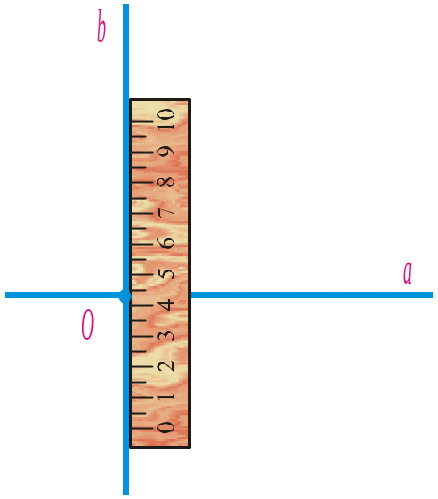
Нехай маємо деяку точку O та деяку пряму a. Як через точку O провести пряму b, перпендикулярну до прямої a?

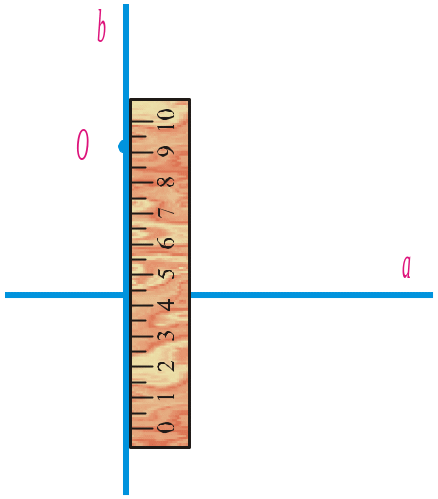
Якщо точка O належить прямій a, то побудова перпендикулярної прямої показана на рисунку 59, якщо точка O не належить прямій a, — на рисунку 60.

Рис. 59
Рис. 60
Усно

1308. Які з прямих, зображених на рисунку 61, є паралельними? Встановіть це «на око», а потім перевірте себе, користуючись лінійкою і косинцем.

1309. Наведіть приклади паралельних прямих на предметах, які є довкола.

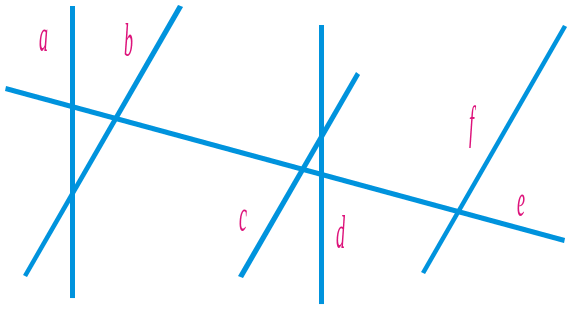
                 Рис. 61        Рис. 62    Рис. 63

1310. На рисунку 62 KLMN — прямокутник. Назвіть протилежні сторони цього прямокутника. Які з його сторін є паралельними?

1311. На рисунку 63 ABCD — прямокутник. Чи паралельні прямі МС і АD?

1312. Які з прямих, зображених на рисунку 64, є перпендикулярними? Встановіть це «на око», а потім перевірте себе, користуючись косинцем або транспортиром.

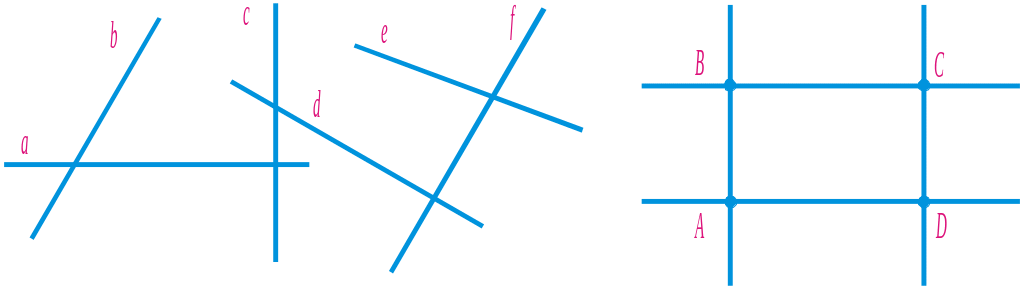                        Рис. 64                                          Рис. 65

1313. На рисунку 65 АВСD — прямокутник. Які з прямих АВ, ВС, СD і DА є перпендикулярними?

1314. Наведіть приклади перпендикулярних прямих на предметах, які є довкола.

Рівень А

1315. Через точку А, що не належить прямій b, проведіть пряму c, паралельну прямій b.

До даної прямої а проведіть дві паралельні прямі b і с. Користуючись лінійкою і косинцем, переконайтеся, що bс.

1317. Накресліть трикутник АВС. Виміряйте довжину сторони АВ та позначте її середину буквою D. Через точку D проведіть пряму, паралельну прямій АС. Переконайтесь, що проведена пряма ділить сторону ВС навпіл.

Накресліть прямокутник KLMN зі сторонами KL = 4 см і LM = 2 см. Через середину сторони KL проведіть пряму, паралельну прямій LM. Переконайтесь, що проведена пряма ділить сторону MN навпіл.

1319. Через точку D, що не належить прямій с, проведіть пряму d, перпендикулярну до прямої с.

Побудуйте деякий трикутник АВС і через точку В проведіть пряму, перпендикулярну до прямої АС.

1321. Прямі АВ і СD перпендикулярні, О — точка їх перетину (рис. 66). Промінь ОМ ділить кут DОВ навпіл. Знайдіть величини кутів МОВ, СОМ і АОМ.

   Рис. 66                                                   Рис. 67

Прямі АВ і СD перпендикулярні, О — точка їх перетину (рис. 67). Кут NОА становить третю частину прямого кута. Знайдіть величини кутів NОА, NОС, DОN і NОВ.

Рівень Б

1323. На рисунку 68 прямі АВ і СD, а також прямі MN і KL перпендикулярні, DOM = 60. Знайдіть величини кутів МОА, АОK, АОN.

На рисунку 68 АВСD, MNKL, кут KОС удвічі менший від кута АОK. Знайдіть величини кутів KОС, СОN, МОС.

1325. На рисунку 68 АВСD, MNKL, кут АОK на 30 більший від кута KОС. Знайдіть величини кутів АОK, KОС, KОВ.

Рис. 68

Здогадайтеся

1326. До магазину завезли 223 л олії у бідонах по 10 л і 7 л. Скільки було бідонів?

Вправи для повторення

1327. Олегові потрібно набрати на комп’ютері 80 сторінок тексту. За перший день він набрав кількості всіх сторінок. Скільки сторінок залишилося набрати Олегові?

1328. Швидкість судна за течією річки дорівнює 28 км/год, а швидкість проти течії становить швидкості за течією. Знайдіть швидкість течії річки.

1329. Периметри квадрата і прямокутника рівні між собою. Знайдіть сторону квадрата, якщо прямокутник завдовжки 18 см і завширшки 14 см.

1330. Ділянка прямокутної форми завдовжки 60 м має площу 750 м². Знайдіть периметр ділянки.