34. Додавання від’ємних раціональних чисел

До раціональних чисел належать додатні числа (цілі та дробові), від’ємні числа (цілі та дробові) та число нуль. Ми вже вивчили дії додавання, віднімання, множення і ділення над додатними раціональними числами і нулем. А тепер навчимося виконувати їх над раціональними числами у випадках, коли обидва числа від’ємні або одне додатне, а інше — від’ємне (числа різних знаків).

Розглянемо приклад.

Нехай у березні фермер узяв у банку кредит 5 тис. грн., а у квітні  ще 3 тис. грн. Тоді за березень i квітень разом фермер узяв 5 + 3 = 8 (тис. грн.) кредиту. Оскільки кредити є боргами фермера перед банком, то позначатимемо їх від’ємними числами: 5 тис. грн.; 3 тис. грн.; 8 тис. грн. Тоді суму кредитів у тисячах гривень за 2 місяці можна записати так:

(5) + (3) = 8.

Який знак має сума двох від’ємних чисел?

Знайдіть модулі доданків і модуль суми. Яка існує залежність між ними?

Бачимо, що сумою чисел 5 і 3 є від’ємне число; модуль суми дорівнює сумі модулів доданків: 8 = 5 + 3. Тому відшукання суми чисел 5 і 3 можна записати так:

(5) + (3) = (5 + 3) = (5 + 3) = 8.

Отже, сумою двох від’ємних чисел є від’ємне число, модуль якого дорівнює сумі модулів доданків. Щоб додати два від’ємні числа, потрібно додати їх модулі й поставити перед одержаним числом знак «–».

Від’ємні числа — борг Борг 5 + борг 3 = борг 8 (–5) + (–3) = –8

У сумі від’ємних доданків перший доданок пишуть, як правило, без дужок. Наприклад: 1,2 + (3,1) = (1,2 + 3,1) = 4,3.

Для додавання від’ємних чисел справджуються переставна і сполучна властивості.

Наприклад, –5 + (–7) = –7 + (–5); (–3 + (–4)) + (–11) = –3 + (–4 + (–11)).

Прочитайте

1. Обчислити:

а) 14 319 + (9848); б) 3  + 

● а) 14 319 + (9848) = 24 167; б) 3  +   = 5

           = 5 =  ●

Для тих, хто хоче знати більше

Домовимося зменшення величини виражати від’ємним числом, а збільшення  додатним. Якщо температура зменшилась на 2С, то можна сказати, що вона змінилась на 2С. Якщо ж температура збільшилась на 2С, то можна сказати, що вона змінилась на 2С. Якщо протягом першої половини дня температура повітря зменшилась на 3С, а протягом другої вона зменшилася на 4С, то протягом дня температура зменшилась на 3 + 4 = 7. За допомогою від’ємних чисел зміну величини температури протягом дня можна записати так: 3 + (4) = 7.

Усно

1011. Обчисліть:

а) 1 + (7); б) 10 + (20); в) (10) + (90);

г) (17) + (13); д) (0,2) + (2,8); е)

Рівень А

Обчисліть:

1012. а) –17 + (–15); б) –99 + (–11); в) –113 + (–17);

г) –35 + (–42); д) –41 + (–115); е) –27 + (–83);

є) –18 + (–43); ж) –11,1 + (–14); з) –17 + (–21,7).

1013. а) 142 + (36); б) 288 + (849); в) 2 318 + (8839);

г) 13,7 + (11,9); д) 80,81 + (7,32); е) 375 + (6,32);

є) ж) з)

а) 83 + (28); б) 793 + (287); в) 10 973 + (4908); г) 1,31 + (9,9); д) 8,82 + (9,78); е) 199 + (8,92);

є) ж) з)

1015. а) 48 + (205 + (853)); б) (9,3 + (2,77)) + (26,93).

а) (17 + (154)) + (909); б) 7,56 + (6,5 + (23,04)).

1017. Знайдіть значення виразу 1,2 + (а), якщо а = 5; а = 17,9; а = 

Знайдіть значення виразу 4,5 + а, якщо а = 4,5; а = 26,8.

1019. Поставте замість зірочки знак «<» або «>» так, щоб утворилась правильна нерівність:

а) 32 + (19)  63; б) 83 + (38)  100.

Рівень Б

Обчисліть:

1020. а)   + (2,4); б) 0,75 + 

в)   + (0,43 + (5,38)); г)

а)   + (1,5); б)

1022. До суми чисел і додайте число, протилежне числу .

До числа, протилежного числу 2,3, додайте суму чисел  і  .

1024. За перший день рівень води в річці змінився на 9 см, за другий  на 8 см, а за третій  на 6,5 см. На скільки сантиметрів змінився рівень води за три дні?

Протягом першої половини дня температура повітря змінилась на 1,5С, а протягом другої  на 3,5С. На скільки градусів змінилась температура повітря протягом дня?

Здогадайтеся

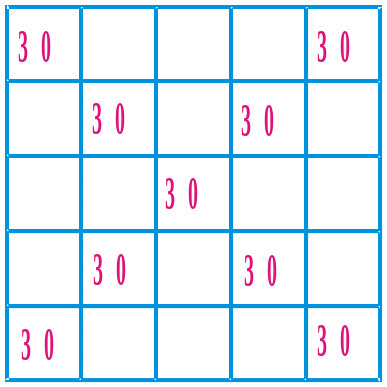
1026. У вільні клітинки квадрата впишіть числа 30 або 5 так, щоб сума чисел у кожному рядку та кожному стовпці дорівнювала 100.

Вправи для повторення

1027. Обчисліть:

а) 15,82  0,25 + 14  7,3 + 0,31   ;

б) 0,3  14,8 + 9  2,3  0,32  0,25.

1028. Скільки тонн сіна вийде із 2,7 т трави, якщо при сушінні трава втрачає 75% своєї маси?

1029. Майстер виготовляє протягом зміни 50 деталей, а учень  40 деталей. На скільки відсотків продуктивність праці майстра вища від продуктивності праці учня?

1030. Скільки грамів солі потрібно додати до 160 г води, щоб одержати 20%-й розчин солі?