Завдання для самоперевірки і рівень

1. Знайдіть відношення чисел: 20 до 5.

а) 15; б) 4; в)  ; г) 5.

2. Чи є правильною пропорція 1,2 : 5 = 22 : 100?

а) Так; б) ні; в) не знаю; г) це не пропорція.

3. Знайдіть x, якщо

а) 2; б) 3,5; в) 3; г) 35.

4. Із 24 кг свіжих слив отримують 8 кг сушених. Скільки сушених слив отримають із 36 кг свіжих?

а) 24 кг; б) 9 кг; в) 16 кг; г) 12 кг.

5. Як називають фігури, зображені на кожному з рисунків?

а)	б)	в)

6. Знайдіть довжину кола радіуса r, якщо r = 5 см.

а) 31,4 см²; б) 15,7 см; в) 3,14 см; г) 31,4 см.

Іі рівень

7. Розв’яжіть рівняння 2,6 : x = 13 : 20.

8. Вкладник вніс до банку 600 грн. під 15% річних. На скільки більше грошей буде на рахунку вкладника через рік?

9. Знайдіть площу круга радіуса r, якщо r = 4 см.

Ііі рівень

10. Розв’яжіть рівняння (x – 7) : 0,2 = 15 : 4.

11. До магазину завезли 3 т 200 кг борошна вищого та першого ґатунків, до того ж, борошна першого ґатунку завезли 2 т 400 кг. Скільки відсотків від усього борошна становить борошно вищого ґатунку?

12. Швидкість легкового автомобіля дорівнює 80 км/год, а вантажного — 60 км/год. На скільки відсотків швидкість вантажного автомобіля менша від швидкості легкового?

IV рівень

13. З першої ділянки зібрали 21 ц помідорів, а з другої  у разу більше. Скільки відсотків усіх помідорів зібрали з першої ділянки?

14. У воді розчинили 300 г солі та одержали 15%-й розчин солі. До розчину долили 500 г води. Скільки відсотків солі містить новий розчин?

15. Виконайте необхідні вимірювання й обчисліть площу фігури, зображеної на рисунку.

§ 5. Раціональні числа. Додавання і віднімання раціональних чисел

30. Додатні та від’ємні числа. Число 0

Розглянемо кілька прикладів.

1. Біля табору туристів дорога проходить із заходу на схід (див. рис. 25). Туристи вийшли з табору і рухаються дорогою зі швидкістю 5 км/год.

Де перебуватимуть туристи через годину?

Щоб встановити місцезнаходження туристів через годину після їх виходу з табору, потрібно знати, на захід чи на схід від табору вони рухаються.

Якщо туристи рухаються на схід, то через годину вони будуть у пункті А. Про пункт А можна сказати, що він розташований на відстані 5 км на схід від пункту О.

Рис. 25

Якщо туристи рухаються на захід, то через годину вони будуть у пункті В. Про пункт В можна сказати, що він розташований на відстані 5 км на захід від пункту О.

Отже, положення туристів відносно табору можна задати числом і напрямом: 5 км на схід від пункту О; 5 км на захід від пункту О.

2. Увечері господиня залишила біля криниці відро з водою. Наступного ранку температура повітря надворі була 4. Що у відрі: вода чи лід?

Щоб дати відповідь на поставлене запитання, потрібно знати, що показує термометр — 4 тепла чи 4 морозу. Якщо термометр показує 4 тепла, то у відрі вода. Про таку температуру ще кажуть: 4 вище нуля, або плюс 4, пишуть: +4. Якщо термометр показує 4 морозу, то у відрі лід. Про таку температуру ще кажуть: 4 нижче нуля, або мінус 4, пишуть: – 4.

	Отже, згадану температуру можна задавати числом зі знаком «+» або «–»:  + 4;  – 4. Температура може дорівнювати і +15, +7,6, –12, – 1,5 тощо. Числа зі знаком «+» розміщені на шкалі термометра (рис. 26) вище нуля, а числа зі знаком «–»  нижче нуля. Числа зі знаком «+» називають додатними. Наприклад: +2; +8,5;  додатні числа. Числа зі знаком «–» називають від’ємними. Наприклад: –1, –3,2; –  від’ємні числа. Число 0 відділяє додатні числа від від’ємних. Воно є ні від’ємним, ні додатним.		Рис. 26
Записуючи додатні числа, знак «+», як правило, опускають i, наприклад, замість +4 пишуть 4. При цьому розуміють, що +4 = 4, тобто +4 i 4  це різні позначення одного й того ж числа. Від’ємні числа визна­чають не лише температуру. Ними, наприклад, можна задавати положення деякого місця земної поверхні відносно рівня моря (див. рис. 27).		Рис. 27

Прочитайте

1. У зошиті у клітинку накреслили горизонтальну пряму і позначили на ній точку О. Точка А лежить ліворуч від точки О на 3 клітинки. Точку А змістили праворуч на 5 клітинок й одержали точку В. Яке положення точки В відносно точки О?

Рис. 28

 Точка В лежить на 2 клітинки праворуч від точки О. 

Усно

889. Прочитайте числа: 4,2; –3; 1000; 0; –2,87; Які з них є: а) від’ємними; б) додатними?

890. Вкажіть покази термометрів, зображених на рисунку 29.

Рис. 29 891. Прямолінійна ділянка шосе проходить з півночі на південь (рис. 30). Охарактеризуйте положення автомобіля відносно станції О, якщо він перебуває в пункті А; у пункті В.

Рис. 30

892. Іра зайшла в ліфт дванадцятиповерхового будинку на сьомому поверсі, проїхала 4 поверхи і вийшла. На якому поверсі вийшла Іра?

893. Якщо мале підприємство має на рахунку в банку 5000 грн., то кажуть, що воно має +5000 грн. Якщо ж підприємство взяло у банку 5000 грн. кредиту, то кажуть, що воно має –5000 грн. Скільки грошей має мале підприємство, якщо воно: а) має на рахунку 700 грн.; 1500 грн.; б) взяло у банку кредит 750 грн.; 3000 грн.?

Рівень А

894. Запишіть за допомогою чисел зі знаками «+» або «–» повідомлення служби погоди: а) 15 градусів тепла; б) 2 градуси морозу; в) 20 градусів морозу; г) 7 градусів тепла.

Запишіть за допомогою знаків «+» або «–» положення вершин гір і впадин морів відносно рівня моря: а) висота гори Говерла 2061 м; б) висота гори Еверест 8848 м; в) найбільша глибина Чорного моря 2211 м; г) найбільша глибина Аравійського моря 5803 м.

896. Якщо у футбольному турнірі команда забила 8 м’ячів, а пропустила 5, то ця команда забила на 3 м’ячі більше, ніж пропустила. У такому випадку кажуть, що різниця забитих і пропущених командою м’ячів дорівнює +3. Якщо ж навпаки, команда забила 5 м’ячів, а пропустила 8, то різниця забитих і пропущених м’ячів дорівнює –3. Заповніть таблицю.

Команда	Забито м’ячів	Пропущено м’ячів	Різниця м’ячів
«Зоря» «Нива» «Лисоня» «Бровар»	18 11 10 8	9 8 12 18

897. У зошиті у клітинку накресліть горизонтальну пряму і позначте на ній деяку точку О. Позначте на цій прямій точки А, В, С, D такі, що:

а) точка А лежить праворуч від точки О на 7 клітинок;

б) точка В лежить ліворуч від точки О на 5 клітинок;

в) точка С лежить праворуч від точки А на 2 клітинки;

г) точка D лежить ліворуч від точки В на 2 клітинки.

898. Точка А лежить праворуч від точки О на 5 клітинок. Точку А змістили праворуч на 3 клітинки й одержали точку В. Яке положення точки В відносно точки О?

Точка С лежить ліворуч від точки О на 7 клітинок. Точку С змістили праворуч на 3 клітинки й одержали точку А. Яке положення точки А відносно точки О?

900. Накресліть горизонтальну пряму і позначте на ній деяку точку О. Позначте точку М, яка лежить праворуч від точки О на 4 клітинки, та точки N і K, які лежать на відстані 6 клітинок від точки М. Яке положення точок N і K відносно точки О?

Точка А лежить праворуч від точки О на 5 клітинок, а точка О  праворуч від точки В на 3 клітинки. Скільки клітинок містить відрізок АВ?

Рівень Б

902. Заповніть таблицю.

Дата	Температура повітря о 12 год	Зміна температури через 8 год	Температура повітря о 20 год
3.09 7.09 15.09 17.09 5.11 1.12 3.12 8.12	+18С +12С +11С +10С +3С –2С –5С –7С	Знизилась на 5С Підвищилась на 1С Знизилась на 2С Підвищилась на 3С Знизилась на 4С Підвищилась на 2С Підвищилась на 3С Знизилась на 5С	+13С

903. Села A, B, C і D розташовані на прямолінійному шляху, що йде з півночі на південь. Відомо, що село A розташоване південніше від села B на 12 км, село С  північніше від села В на 6 км, село D  південніше від села С на 10 км. Із села B у південному напрямі виїхав велосипедист і, проїхавши 6 км, зупинився. Чи проїхав велосипедист якесь із названих сіл? Вкажіть положення велосипедиста відносно сіл А та D.

Однією трасою, але у протилежних напрямах, їдуть автомобіль зі швидкістю 72 км/год і мотоцикліст зі швидкістю 48 км/год. У даний момент відстань між ними дорівнює 24 км. Якою може бути відстань між автомобілем і мотоциклістом через 10 хв?

Протягом дня равлик відповз від гілки вгору по дереву на 32 см, а протягом ночі опустився на: а) 23 см; б) 41 см. На скільки сантиметрів від гілки і в якому напрямі від неї перемістився равлик протягом доби?

906. Підводний човен спочатку плив на глибині 250 м, далі опустився ще на 300 м, а потім піднявся на 350 м. На якій глибині опинився підводний човен?

Здогадайтеся

907. До річки підійшли три генерали: Грізний, Лихий і Суворий, кожен зі своїм слугою. Їм потрібно переправитися на інший берег річки на двомісному човні, до того ж, кожен генерал заборонив своєму слузі бути поруч з іншими генералами під час його відсутності. Як організувати переправу?

Цікаві розповіді Про від’ємні числа

Першими зустрілися з потребою у від’ємних числах географи, моряки, картографи, оскільки їм необхідно було характеризувати положення міст, розміщених, з одного боку, на північ чи південь від головного міста, а з іншого — на захід чи схід від нього. Головними місцями відліку були вибрані екватор і Грінвічський меридіан. Пізніше в археологів, істориків виникла потреба характеризувати шкалу часу, починаючи від року народження Ісуса Христа.

Геологам потрібно було характеризувати нерівності земного рельєфу, а саме — висоту гір, глибину впадин морів і океанів, приймаючи за початок рівень моря (рис. 31).

Фізикам, інженерам, астрономам, лікарям потрібно було вимірювати температуру. У XVIII ст. шведським ученим Цельсієм (1701 – 1744) була створена вимірювальна шкала, у якій за початок відліку (нуль) була прийнята температура плавлення льоду.

Від’ємні числа люди винайшли значно пізніше, ніж натуральні числа i звичайні дроби. До ідеї від’ємного числа першими прийшли китайці у ІІ ст. до н. е. Необхідність введення нових на той час чисел обумовлювалась проблемами самої математики  від’ємні числа потрібні були для розв’язування рівнянь. Потім індуси дали тлумачення додатних i від’ємних чисел у вигляді «майна» i «боргу».

У Європі від’ємні числа почали використовувати, починаючи з ХІІ ст. Однак ставились до від’ємних чисел з недовірою, називаючи їх «фіктивними», «абсурдними», «хибними» тощо. «Справжніми» числами вважали лише додатні числа. Тільки у XVII ст., коли видатний французький математик Рене Декарт (1596  1650) запропонував зображувати від’ємні та додатні числа точками координатної прямої, від’ємні числа були повністю визнані й стали повноправним атрибутом математики.

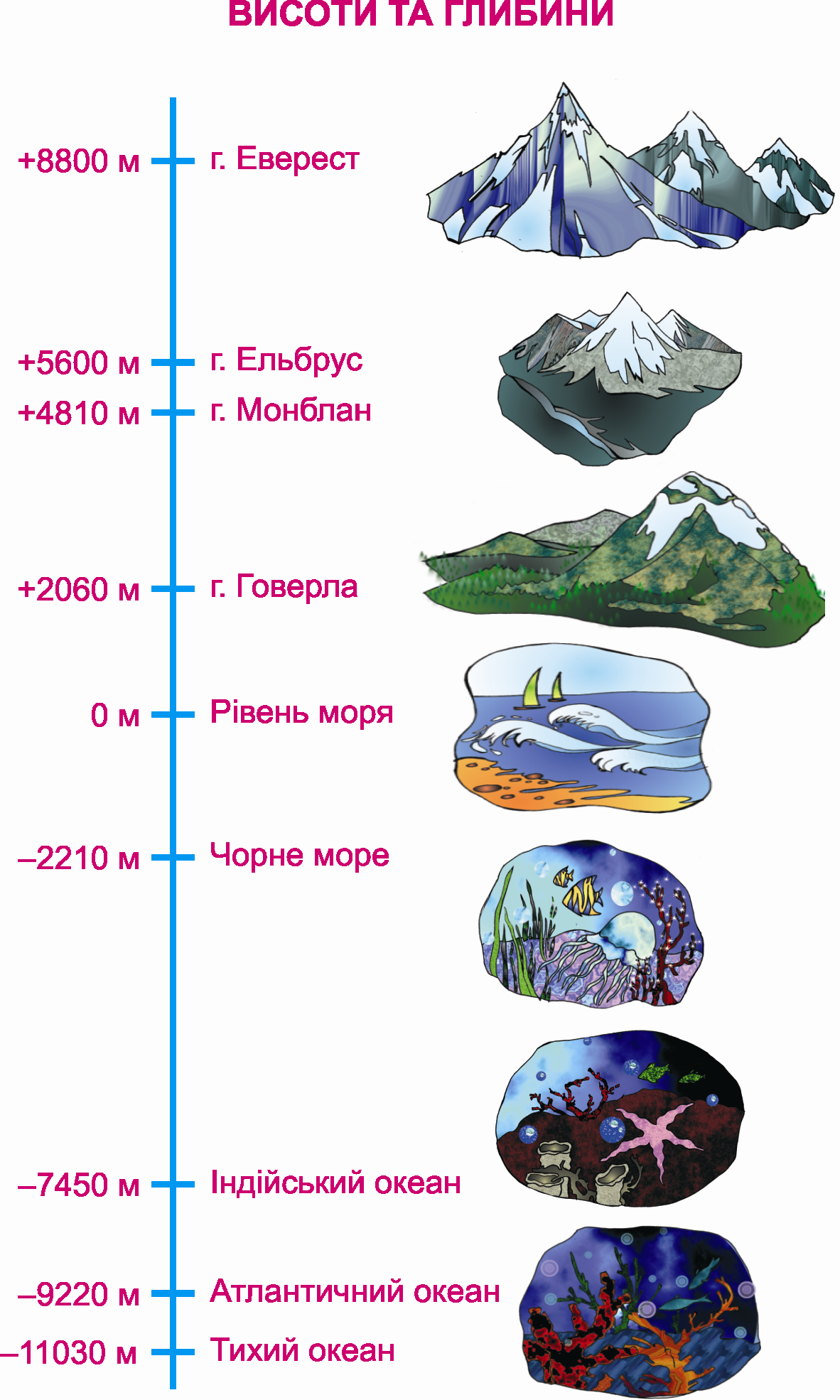
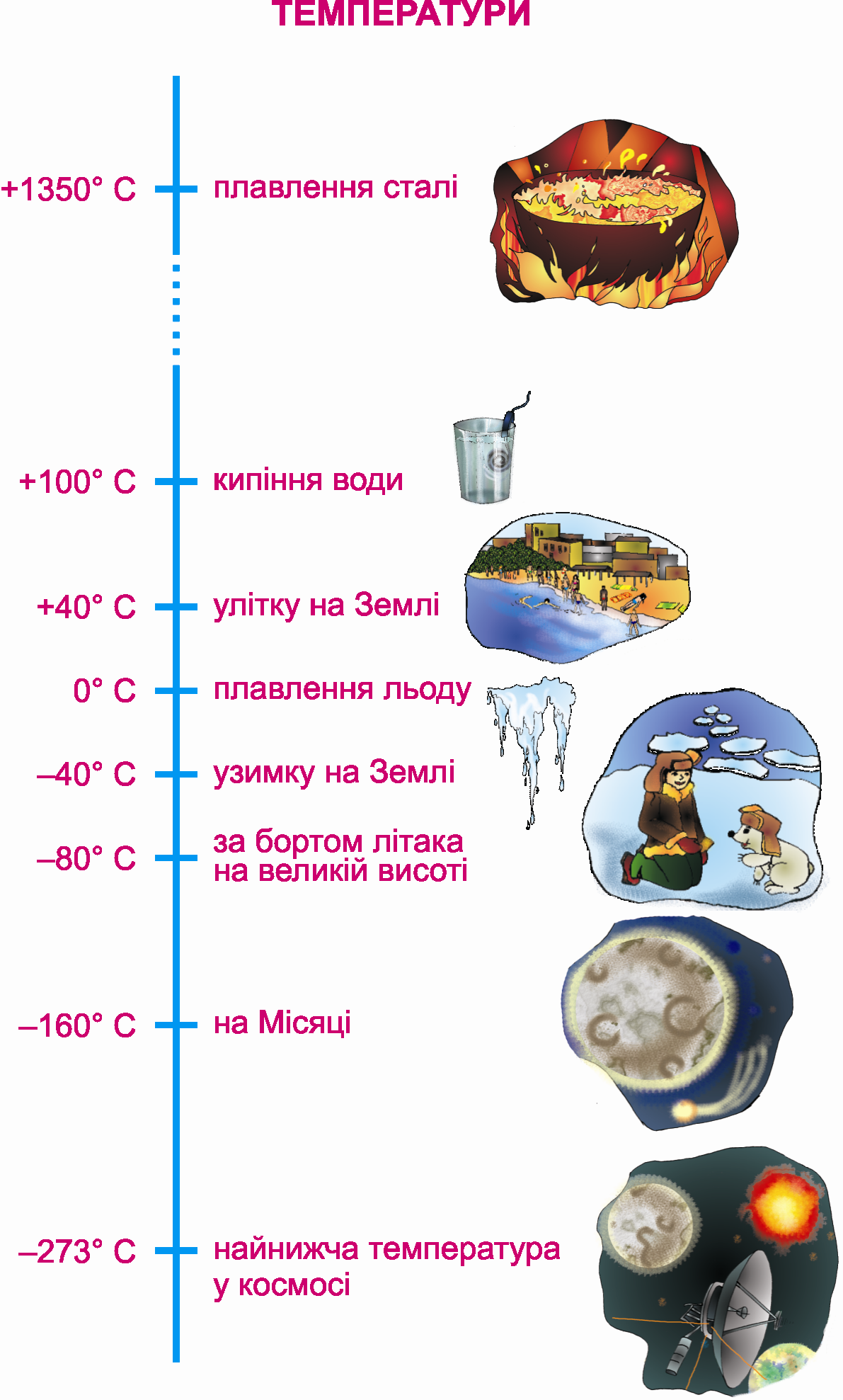Рис. 31

Вправи для повторення

908. Виконайте дії:

а) 376  208 – 134 415 : 435; б) 342 342 : 38 + 123  217;

в) г) (96,6 + 98,6) : 6,4 – 0,05 : 0,5.

909. Накресліть координатний промінь, узявши за одиничний відрізок 5 клітинок зошита. Позначте на ньому точки: А(2); В(0,8); С(1,4); D ; Е .

910. Прямий кут поділили променем на два кути так, що один з них у 4 рази більший від іншого. Скільки градусів має кожний з утворених кутів?