27. Коло. Довжина кола

Уявлення про коло дають кермо автомобіля, обруч, каблучка тощо. Нарисуємо коло. Для цього позначимо на площині деяку точку O. Візьмемо циркуль, поставимо його ніжку з голкою в точку O і розхилом у 3 см іншою ніжкою циркуля опишемо фігуру. Одержимо коло із центром у точці O. Усі точки кола розміщені на відстані 3 см від центра.

Сполучимо центр кола з довільною точкою A цього кола відрізком (рис. 5). Відрізок OA, а також його довжину називають радіусом кола. Радіус побудованого кола дорівнює 3 см. Відрізок, що сполучає дві точки кола і проходить через його центр, а також довжину цього відрізка називають діаметром. Діаметр кола удвічі довший від радіуса цього кола.

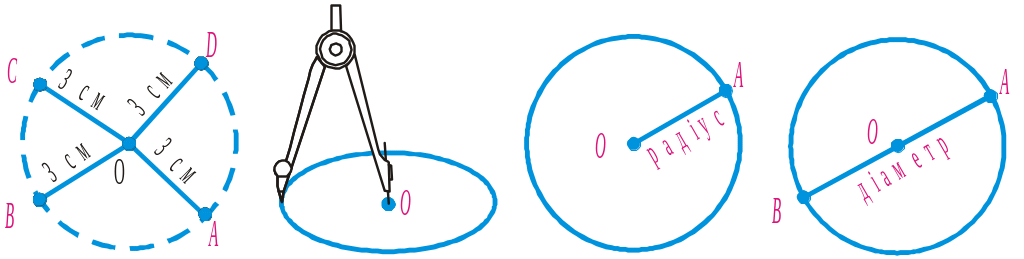Рис. 5

Дві точки A та B, що лежать на колі (рис. 6), розбивають його на дві частини. Кожну із цих частин називають дугою кола. Точки A та B — кінці цих дуг. Якщо точки A та B є кінцями діаметра, то вони розбивають коло на дві рівні частини, кожну з яких називають півколом.

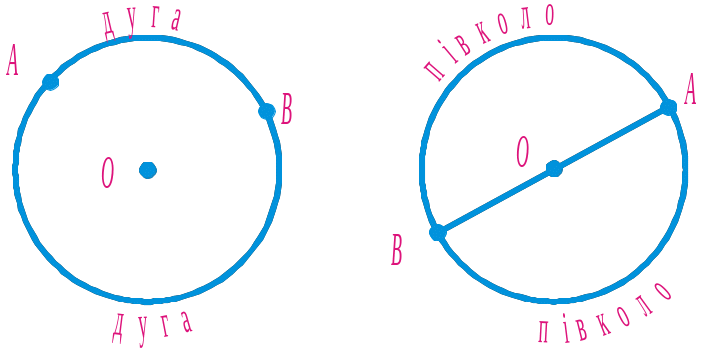Рис. 6

Практична робота

Тема роботи. Довжина кола.

Обладнання. Циркуль, лінійка, нитка.

Хід роботи

1. Будуємо коло, радіус якого дорівнює 2 см.

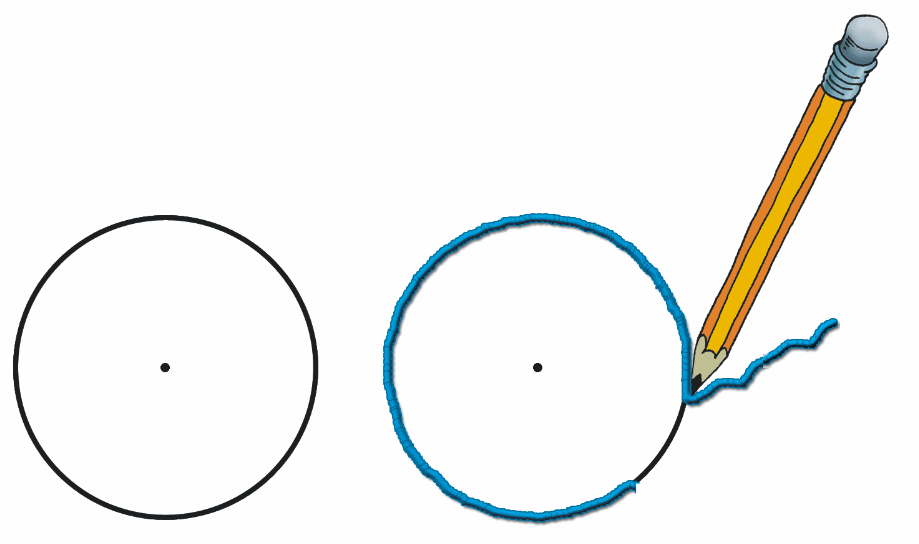Рис. 7

2. Накладаємо на коло нитку (див. рис. 7).

3. Ставимо ручкою відмітку на нитці в тій точці, у якій нитка збігається зі своїм початком.

4. Розгортаємо нитку та вимірюємо її довжину до відмітки. Ця довжина дорівнює довжині кола.

Рис. 8

5. Діаметр кола d дорівнює 4 см: d = 4 см; довжина кола С дорівнює: С = ... .

6. Знаходимо відношення

Виявляється, що для всіх кіл відношення довжини кола до довжини його діаметра є одним і тим же числом. Це число позначають грецькою буквою  (читають: «пі»), воно записується нескінченним десятковим дробом  = 3,1415926… . Отже, = , звідки

С = d.

Довжина кола дорівнює добутку числа  й діаметра кола.

Оскільки діаметр кола дорівнює двом радіусам, то довжина кола радіуса r дорівнює 2r. Маємо ще одну формулу для довжини кола:

С = 2r.

Далі для розрахунків ми, як правило, округлюватимемо число  до сотих:   3,14, а в окремих випадках братимемо   .

Прочитайте

1.  Накреслити коло, радіус якого дорівнює 2 см. Де лежить точка, розміщена від центра на відстані 1 см; 2 см; 3 см? Чому дорівнює діаметр кола?

 Точка A, відстань від якої до центра дорівнює 2 см (рис. 9), належить колу. Точка B, відстань від якої до центра дорівнює 1 см (рис. 9), лежить усередині кола. Точка C, відстань від якої до центра дорівнює 3 см (рис. 9), лежить зовні кола. Діаметр кола: 2  2 = 4 (см). 

Рис. 9

2. Знайти довжину кола, радіус якого дорівнює 1,5 см.

 С = 2r  2  3,14  1,5 = 9,42 (см). 

Усно
791. На рис. 10 зображено коло радіуса 12 мм. а) Які відрізки, зображені на цьому рисунку, є радіусами кола? б) Чому дорівнює діаметр кола? в) Порівняй з радіусом кола довжини відрізків ОА, ОВ, ОС.	Рис. 10

792. Знайдіть довжину кола, діаметр якого дорівнює 10 см.

793. Знайдіть довжину кола, радіус якого дорівнює 5 дм.

Рівень А

794. Позначте у зошиті точку O. Накресліть коло довільного радіуса із центром у цій точці. Виміряйте радіус кола.

Накресліть коло, діаметр якого дорівнює 36 мм.

796. Накресліть коло із центром O радіусом 25 мм та пряму AB, яка перетинала б це коло у двох точках M і K. На якій відстані від центра O лежать точки M і K?

797. Накресліть коло із центром O радіусом 3 см. Позначте на ньому точку A і проведіть коло з центром A і тим же радіусом. Чи проходить друге коло через точку O?

Накресліть відрізок AB завдовжки 4 см. Узявши точки A та B за центри, проведіть два кола, радіуси яких дорівнюють 25 мм. Позначте точки перетину цих кіл буквами M і K. На якій відстані лежать точки M і K від точок A та B?

Накресліть коло, радіус якого дорівнює 3 см. Де лежить точка, розміщена від центра на відстані 25 мм; 30 мм; 35 мм?

800. Дано два кола, радіуси яких дорівнюють 1 см і 3 см, із центром в одній і тій же точці О. Промінь із початком у точці О перетинає ці кола в точках А та В. Знайдіть довжину відрізка АВ.

Знайдіть довжину кола:

801. а) діаметр якого дорівнює: 2,5 см; 36 см; 0,24 м; б) радіус якого дорівнює: 5 см; 3,6 см; 0,4 м.

а) діаметр якого дорівнює: 3 см; 0,8 дм; 0,12 м; б) радіус якого дорівнює: 6 см; 1,4 дм; 1,2 м.

Виміряйте діаметри і довжини верхніх країв двох різних склянок. Знайдіть відношення довжин кіл до відповідних діаметрів (результати округліть до десятих).

804. Планер пролетів чотири рази по колу, радіус якого дорівнює 25 м. Скільки метрів пролетів планер?

805. Довжина кола дорівнює 11 м. Знайдіть діаметр кола (  ).

Довжина кола дорівнює 33 см. Знайдіть радіус кола (  ).

807. Який шлях подолає в пустелі верблюд, пройшовши коло, радіус якого дорівнює 3 км?

Рівень Б

808. Хвилинна стрілка годинника описала півколо. За який час вона це зробила? За який час вона повернеться на чверть кола?

Годинна стрілка описала півколо. За який час вона зробила такий поворот?

810. Накресліть відрізок AB завдовжки 4 см. Побудуйте точки, відстань від яких до точки А дорівнює 3 см, а до точки В — 2 см.

Проведіть деяку пряму a та виберіть точку А, яка не лежала б на цій прямій. Як на прямій a знайти точки, відстань до яких від точки А дорівнює 3 см? Чи завжди такі точки існують?

812. Накресліть відрізок AB завдовжки 4 см. Побудуйте коло найменшого радіуса, яке проходить через точки A та B.

813. Накресліть коло, радіус якого дорівнює 2 см. Позначте точку A всередині цього кола. Знайдіть на колі точку, відстань від якої до точки A найменша (найбільша). Порівняйте ці відстані з радіусом.

Найбільша і найменша відстані від точки K, яка лежить усередині кола, до точок цього кола дорівнюють 15 мм і 5 мм відповідно. Знайдіть радіус та діаметр кола.

815. За скільки часу можна облетіти на літаку Землю вздовж екватора на висоті 10 км, рухаючись зі швидкістю 1200 км/год? Результат округліть до 0,1 год. (Радіус екватора наближено дорівнює 6370 км.)

816. Супутник рухається по коловій орбіті на висоті 36 000 км і робить повний оберт навколо Землі за 24 год. З якою швидкістю рухається супутник, якщо радіус Землі наближено дорівнює 6400 км?

Радіус кола збільшили з 10 см до 11 см. На скільки збільшилась довжина кола?

818. Довжина кола збільшилась від 157 см до 226,08 см. На скільки збільшився радіус кола? 819. Із прямокутника вирізали частину, обмежену півколом (рис. 11). Зробіть необхідні вимірювання і знайдіть периметр утвореної фігури.

Рис. 11

820. Діаметр колеса тепловоза дорівнює 80 см. За 2 хв колесо робить 800 обертів. Яка швидкість тепловоза в кілометрах за годину? Результат округліть до десятих км/год.

Здогадайтеся

821. На шалькових терезах потрібно зважити 13 кг цукру, маючи лише гирю 1 кг. Якою найменшою кількістю зважувань це можна зробити?

Вправи для повторення

822. У саду росте 180 фруктових дерев. Серед них 120 яблунь, 30% усіх інших дерев становлять вишні, а решта — груші. Скільки груш росте в саду?

823. У трьох містах разом є 285 тис. жителів. У першому місті є 120 тис. жителів, у другому — 80% тієї кількості, що в першому. Скільки жителів у третьому місті?

824. У парку першого дня посадили 96 дерев, а другого — 72 дерева, що становить 80% від кількості дерев, посаджених третього дня. Скільки дерев посадили за три дні?

825. Розв’яжіть рівняння:

а) (x + 0,05) · 0,6² = 5,4; б) (1,5 – х) · 7,2 = 1,2².