
- •Галина Янченко, Василь Кравчук Математика
- •Юні друзі!
- •§ 1. Подільність чисел
- •1. Дільники натурального числа
- •2. Ознаки подільності на 2, 5 і 10
- •50*. Використовуючи цифри 0, 2, 5, 7, 8 не більше одного разу, запишіть чотирицифрове число, що ділиться на 4; на 25.
- •3. Ознаки подільності на 9 і на 3
- •4. Прості й складені числа
- •5. Розкладання натуральних чисел на прості множники
- •6. Найбільший спільний дільник
- •7. Кратні натурального числа. Найменше спільне кратне
- •Пам’ятка до §1
- •Запитання для самоперевірки і повторення
- •Завдання для повторення § 1
- •§ 2. Додавання і віднімання звичайних дробів
- •8. Основна властивість дробу
- •9. Застосування основної властивості дробу а) Скорочення дробу
- •Б) Зведення дробу до нового знаменника
- •231. Скоротіть неправильні дроби та виділіть їх цілі частини:
- •10. Зведення дробів до спільного знаменника. Порівняння дробів
- •261. Розмістіть у порядку зростання дроби: ; ; ; ; ; .
- •265. Розмістіть дроби в порядку спадання: ; ; ; ; ; .
- •11. Додавання і віднімання дробів з різними знаменниками
- •301. Маса першої деталі дорівнює кг, а другої на кг менша. Знайдіть масу другої деталі.
- •303. За перший день заасфальтували км дороги, а за другий на км менше. Скільки кілометрів дороги заасфальтували за два дні?
- •305. За перший день Ігор прочитав кількості сторінок книжки, за другий , а за третій решту. Яку частину книжки прочитав Ігор за третій день?
- •Пам’ятка до §2
- •Запитання для самоперевірки і повторення
- •Завдання для повторення § 2
- •13. Задачі на множення дробів
- •417. Збільште число 100 на 20%, а одержане при цьому число зменште на 20%.
- •14. Взаємно обернені числа
- •436. Чи існує число, обернене до нуля?
- •15. Ділення звичайних дробів
- •16. Задачі на ділення дробів
- •486. На присадибній ділянці зібрали 8 кг огірків, що становить 40% зібраних овочів. Скільки кілограмів овочів зібрали?
- •17. Перетворення звичайних дробів у десяткові. Періодичні десяткові дроби
- •18. Вправи на всі дії зі звичайними дробами
- •19. Текстові задачі
- •Пам’ятка до §3
- •21. Випадкові події
- •22. Імовірність випадкової події
- •23. Пропорція
- •24. Пряма пропорційна залежність
- •І спосіб
- •Іі спосіб
- •20 Частин х кг;
- •3 Частини 1,8 кг.
- •704. На плані з масштабом 1 : 100 кімната має розміри 6,8 см 4,5 см. Скільки потрібно фарби для фарбування підлоги в цій кімнаті, якщо для фарбування 7,5 м2 підлоги пішло 0,75 кг фарби?
- •25. Відсоткове відношення
- •26. Відсоткові розрахунки
- •27. Коло. Довжина кола
- •Практична робота
- •Хід роботи
- •28. Круг. Площа круга
- •Практична робота
- •Хід роботи
- •828. А) радіус якого дорівнює 5 см; 11 см; 0,3 дм; б) діаметр якого дорівнює 0,6 м; 7 м.
- •29. Стовпчасті та кругові діаграми
- •Пам’ятка до §4
- •Запитання для самоперевірки і повторення
- •Завдання для повторення § 4
- •Завдання для самоперевірки і рівень
- •Іі рівень
- •Ііі рівень
- •IV рівень
- •§ 5. Раціональні числа. Додавання і віднімання раціональних чисел
- •30. Додатні та від’ємні числа. Число 0
- •31. Координатна пряма. Раціональні числа
- •32. Модуль числа
- •33. Порівняння чисел
- •34. Додавання від’ємних раціональних чисел
- •35. Додавання двох чисел з різними знаками
- •36. Віднімання раціональних чисел
- •37. Розкриття дужок
- •Пам’ятка до §5
- •Запитання для самоперевірки і повторення
- •Завдання для повторення §5
- •39. Переставна і сполучна властивості множення. Коефіцієнт
- •40. Розподільна властивість множення. Зведення подібних доданків
- •41. Ділення раціональних чисел
- •42. Розв’язування рівнянь
- •43. Розв’язування задач за допомогою рівнянь
- •44. Паралельні та перпендикулярні прямі
- •45. Координатна площина
- •46. Приклади графіків залежностей між величинами
- •Пам’ятка до §6
- •Запитання для самоперевірки і повторення
- •Завдання для повторення §6
- •Завдання для самоперевірки і рівень
- •Іі рівень
- •Ііі рівень
- •IV рівень
- •ЗАвдання за курс математики 6 класу
- •Задачі підвищеної складності Подільність натуральних чисел
- •Відсотки
- •Звичайні дроби
- •Раціональні числа
- •Задачі на складання рівнянь
- •Логічні задачі
- •Предметний покажчик
- •Відповіді
- •Розділ iіі. Пропорції і відношення
- •Розділ IV. Раціональні числа та дії над ними
- •Навчальне видання
- •46010, М. Тернопіль, вул. Поліська, 6а. Тел. 8-(0352)-43-10-31, 43-15-15, 43-10-21.
Пам’ятка до §3
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
Запитання для самоперевірки і повторення
1. Як знайти добуток двох звичайних дробів?
2. Як знайти дріб від числа?
3. Як знайти відсотки від числа?
4. Які числа називають взаємно оберненими? Наведіть приклад.
5. Як поділити один дріб на інший?
6. Як знайти число за його дробом?
7. Як знайти число за його відсотками?
8. Як перетворити звичайний дріб у десятковий?
9. Наведіть приклад нескінченного періодичного десяткового дробу.
Завдання для самоперевірки
І рівень
1. Виконайте
множення
![]() .
.
а)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]()
2. Виконайте
ділення
![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
3. Розв’яжіть
рівняння
![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
4. Розв’яжіть
рівняння
![]() .
.
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
5. У книзі 300 сторінок. Учень прочитав книги. Скільки сторінок прочитав учень?
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]()
6. Запишіть десятковим дробом .
а) 0,4; б) 0,2; в) 2,5; г) 0,25.
ІІ рівень
7. Знайдіть
значення виразу
![]() .
.
8. Швидкість вантажного автомобіля дорівнює 60 км/год, що становить швидкості легкового. Знайдіть швидкість легкового автомобіля.
9. У класі є 30 учнів, 20% з них навчаються у музичній школі. Скільки учнів навчається у музичній школі?
ІІІ рівень
10. Знайдіть
значення виразу
![]() .
.
11. Периметр прямокутника дорівнює 6,4 см, його довжина становить периметра. Знайдіть ширину прямокутника.
12. Швидкість течії річки дорівнює 3 км/год, що становить 15% швидкості катера у стоячій воді. Знайдіть швидкість катера за течією річки i проти течії.
IV рівень
13. Знайдіть
значення виразу
![]()
14. Після того як Сергій витратив 40% усіх своїх грошей на купівлю книжки, а решти на купівлю зошитів, у нього залишилося 3 грн. Скільки грошей було в Сергія спочатку?
15. Сума двох чисел дорівнює 15,3. Знайдіть ці числа, якщо одне з них становить 50% іншого.

§ 4. ПРОПОРЦІЇ і ВІДНОШЕННЯ
20. Відношення. Основна властивість відношення
Задача. Для класу закупили 90 зошитів, з них 60 у клітинку, а решта у лінійку. У скільки разів усіх зошитів більше, ніж зошитів у клітинку? Яку частину всіх зошитів становлять зошити у клітинку?
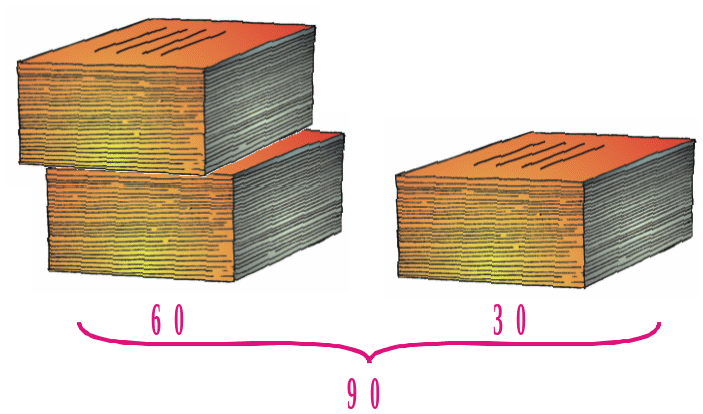
Щоб знайти, у скільки разів усіх зошитів більше, ніж зошитів у клітинку, потрібно 90 поділити на 60, тобто знайти частку чисел 90 і 60:
90 : 60 = ![]() =
=
= 1,5.
=
=
= 1,5.
Отже, усіх зошитів в 1,5 разу більше, ніж зошитів у клітинку. Частка чисел 90 і 60 вказує, у скільки разів число 90 більше від числа 60.
Відповімо на друге
запитання задачі. Оскільки всього є
90 зошитів, то
1 зошит це
![]() частина усіх зошитів, а 60 зошитів
це
частина усіх зошитів, а 60 зошитів
це
![]() ,
або
усіх зошитів. Отже, зошити у клітинку
становлять
усіх
зошитів. Цю ж відповідь ми одержали б,
одразу поділивши 60 на 90. Тому частка
чисел 60 і 90 вказує, яку частину становить
число 60 від числа 90.
,
або
усіх зошитів. Отже, зошити у клітинку
становлять
усіх
зошитів. Цю ж відповідь ми одержали б,
одразу поділивши 60 на 90. Тому частка
чисел 60 і 90 вказує, яку частину становить
число 60 від числа 90.
Щоб відповісти на обидва запитання задачі, нам доводилося шукати частки двох чисел. Такі частки називають відношеннями двох чисел: частку 90 : 60 = 1,5 називають відношенням числа 90 до числа 60; частку 60 : 90 = відношенням числа 60 до числа 90.
|
Відношенням двох чисел називають частку цих чисел. Відношення вказує, у скільки разів одне число більше від іншого, або яку частину становить одне число від іншого. |
Якщо є дві величини,
виміряні однією і тією ж одиницею
вимірювання, то відношенням цих величин
називають відношення їхніх числових
значень. Наприклад, відношення 6 км
до 10 км
дорівнює 6 : 10 = ![]() відношення 10 кг
до 2 кг
дорівнює 10 : 2 = 5.
Знайти відношення 600 г до 2 кг можна
так: 2 кг = 2000 г, тому шукане
відношення
600 : 2000 = 0,3
(або 600 г = 0,6 кг,
тому шукане відношення
0,6 : 2 = 0,3).
відношення 10 кг
до 2 кг
дорівнює 10 : 2 = 5.
Знайти відношення 600 г до 2 кг можна
так: 2 кг = 2000 г, тому шукане
відношення
600 : 2000 = 0,3
(або 600 г = 0,6 кг,
тому шукане відношення
0,6 : 2 = 0,3).
Оскільки відношення є часткою, а частка не змінюється, якщо ділене і дільник помножити або поділити на одне й те ж число, відмінне від нуля, то відношення не зміниться, якщо кожне з чисел відношення помножити або поділити на одне й те ж, відмінне від нуля, число. Цю властивість називають основною властивістю відношення. Наприклад:
40 : 32 = 20 : 16 = 10 : 8 = 5 : 4.
На основі цієї властивості можна замінити відношення дробових чисел на відношення натуральних чисел. Наприклад:
1,5 : 2,5 = 15 : 25 = 3 : 5;
![]()
Прочитайте |
|
1. Спортсмен пробіг 100 м за 10 с, а ракета пролетіла 24 км за 3 с. У скільки разів швидкість ракети більша від швидкості спортсмена?
1) 100 : 10 = 10 (м/с) — швидкість спортсмена.
2) 24 : 3 = 8 (км/с) — швидкість ракети.
Знайдемо швидкість ракети у м/с: 8 км/с = 8000 м/с.
3) 8000 : 10 = 800 (разів).
Відповідь. У 800 разів.
Усно |
|
607. Знайдіть відношення чисел: 15 до 5; 10 до 30; 7 до 2. На що вказує кожне із цих відношень?
608. Назвіть
кілька чисел, відношення яких дорівнює
2;
![]() ;
;
![]() .
На що вказує кожне з названих відношень?
.
На що вказує кожне з названих відношень?
Рівень А |
|
Знайдіть відношення:
609. а) 375 до 15; б) 102 до 30; в) 15 до 45; г) 130 до 52;
д) 3,5 до 0,7; е)
0,72 до 1,2; є)
до
![]() ж) 1,4 до
ж) 1,4 до
![]()
610. а) 3 дм до 2 дм; б) 2 дм до 10 см; в) 1 м до 5 дм;
г) 1 т до 25 ц; д) 2 ц до 400 кг; е) 2 грн. до 50 к.
|
а) 18 до
12; б) 4,5 до 1,05; в) 0,5 до
|
г)
![]() до
до
![]() д)
д)
![]() до
до
![]() е)
240 г до
360 г;
е)
240 г до
360 г;
є) 25 см до 4 дм; ж) 2 кг до 8 ц; з) 3 грн. до 120 к.
612. Урожайність пшениці на першому полі — 48 ц із гектара, а на другому 36 ц. У скільки разів урожайність пшениці на першому полі більша від урожайності на другому? Яку частину від урожайності на першому полі становить урожайність на другому?
|
Перша труба завдовжки 3,2 м, а друга 4 м. У скільки разів друга труба довша за першу? Яку частину від довжини другої труби становить довжина першої? |
|
Довжина тролейбусного маршруту дорівнює 10 км, до того ж, 6 км маршруту припадають на околиці, а решта на центральну частину міста. У скільки разів весь маршрут довший за ту його частину, яка припадає на околиці? Яка частина маршруту припадає на околиці? |
615. Бригада заасфальтувала 4,2 км дороги між двома селами, і їй залишилося заасфальтувати ще 1,8 км. Яку частину всієї дороги заасфальтовано; не заасфальтовано? Яку частину від заасфальтованої дороги становить незаасфальтована ділянка? У скільки разів заасфальтована ділянка довша від незаасфальтованої?
Спростіть:
616. а)
50 : 150; б)
150 : 225; в)
18 : 72; г)
![]()
|
а) 125 : 50; б)
17 : 102; в)
112 : 48; г)
|
Замініть відношення дробових чисел відношенням натуральних:
618. а) 0,3 : 0,27;
б) 0,03 : 1,2; в) ![]() г)
г)
![]()
|
а) 1,5 : 0,3; б) 0,02 : 2,2; в) |
620. Із 200 кг молока одержали 50 кг вершків. Яку частину молока становлять вершки?
|
Із 4 т цукрових буряків одержали 840 кг цукру. Яку частину в цукрових буряках становить цукор? |
622. Ділянку засадили картоплею, витративши для цього 80 кг картоплі, а восени з цієї ділянки зібрали 5 ц 20 кг картоплі. У скільки разів зібраний урожай більший від маси картоплі, яку посадили?
|
Довжина ящірки дорівнює 15 см, а крокодила — 4,5 м. У скільки разів крокодил довший від ящірки? |
624. Том Сойєр пофарбував 1,5 м2 паркану, а його друг Бен — на 0,75 м2 більше. У скільки разів більша частину паркану, яку пофарбував Бен, від частини паркану, яку пофарбував Том?
Рівень Б |
|
625. У зоопарку були мавпи різних порід: горили, шимпанзе й орангутанги. Найбільше було вертких шимпанзе, аж 18, поважно походжали горили, кількість яких становила від кількості шимпанзе, спокійно розглядали відвідувачів орангутанги, яких було вдвічі менше, ніж горил. Яку частину всіх мавп становили горили?
626. 0,3 кг сиру коштує 5 грн. 40 к., а 250 г бринзи — 4 грн. У скільки разів кілограм сиру дорожчий від кілограма бринзи?
|
0,4 кг цукерок коштує 4 грн. 80 к., а 200 г печива — 1 грн. 20 к. У скільки разів кілограм цукерок дорожчий від кілограма печива? |
||
|
Андрій пройшов 2 км за 0,5 год, а черепаха проповзла 20 м за 15 хв. У скільки разів швидкість учня більша від швидкості черепахи? |
||
|
Здогадайтеся |
|
|
629. Число 666 збільште у півтора разу, не виконуючи над ним жодних арифметичних дій.
Вправи для повторення |
|
630. Є три види конвертів і п’ять видів марок. Скільки є варіантів вибору одного конверта з маркою?
631. Скількома способами можна розмістити трьох гостей за круглим столом?
632. Розв’яжіть рівняння:
а)
![]() б)
б)
![]() ;
;
в)
![]() ; г)
; г)
![]()
633. У чотирьох цистернах було 38 т бензину. З першої цистерни взяли 2 т бензину, із третьої перелили до другої 1 т, а до четвертої долили 3 т. Скільки бензину стало в чотирьох цистернах?

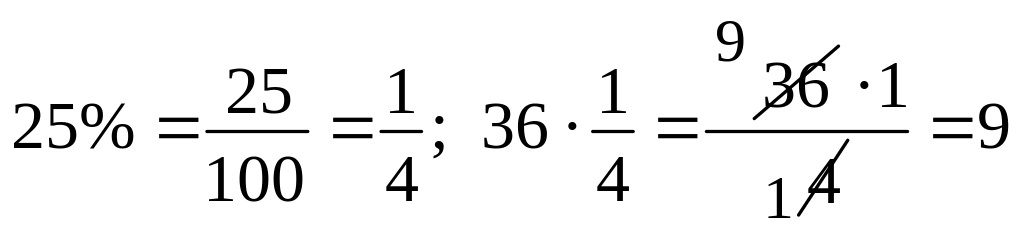 — знайшли 25% від
числа 36.
— знайшли 25% від
числа 36.