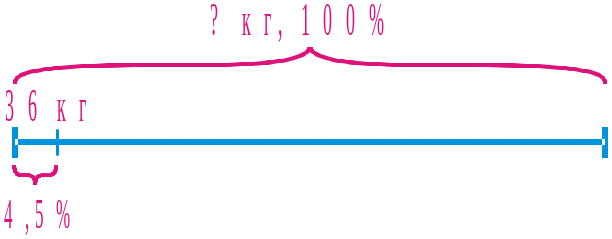16. Задачі на ділення дробів

Задача 1. З дослідної ділянки площею га зібрали 176 ц пшениці. Яка врожайність пшениці на цій ділянці?

Щоб відповісти на запитання задачі, потрібно масу всієї зібраної пшениці поділити на площу ділянки:

(ц).

Отже, врожайність пшениці на цій ділянці  64 ц з гектара.

Такі і подібні задачі, але з натуральними числами або десятковими дробами, ми вже розв’язували раніше і теж за допомогою ділення.

Розв’яжемо тепер за допомогою ділення дробів задачі, які раніше розв’язували іншими способами.

Задача 2. Автомобіль, рухаючись від міста А до міста В, проїхав 60 км, що становить відстані між цими містами. Яка відстань між містами А і В?

Вам відоме таке розв’язання задачі:

1) 60 : 2 = 30 (км)  припадає на відстані;

2) 30  5 = 150 (км)  відстань між містами.

Запишемо розв’язок цієї задачі у вигляді числового виразу (60 : 2)  5, який перетворимо так:

(60 : 2)  5

Отже, дану задачу можна розв’язати діленням на дріб.

У задачі відомо, що відстані  це 60 км, а потрібно знайти всю відстань, тобто в задачі відомо, чому дорівнює дріб від числа, а потрібно знайти саме число.

знайшли число за значенням його дробу

Щоб знайти число за даним значенням його дробу, досить це значення поділити на дріб.

Задача 3. З чайного листа виходить 4,5% чаю. Скільки потрібно взяти чайного листа, щоб отримати 36 кг чаю?

Запишемо відсотки у вигляді дробу: 4,5% = 4,5 : 100 = 0,045.

Потрібно знайти масу чайного листа, якщо 0,045 цієї маси становить 36 кг, тобто потрібно знайти число за даним значенням його дробу:

36 : 0,045 = 800 (кг).

Отже, щоб отримати 36 кг чаю, потрібно взяти 800 кг чайного листа.

Розв’язуючи задачу, ми шукали число, 4,5% якого дорівнює 36, тобто шукали число за його відсотками.

4,5% = 0,045 36 : 0,045 = 800 знайшли число за значенням його відсотків

Щоб знайти число за його відсотками, досить записати відсотки дробом і поділити значення відсотків на одержаний дріб.

Прочитайте

1. Знайти число, якого дорівнює 45.

  

2. Знайти число, % якого дорівнює 14.

  =    

Усно

484. На присадибній ділянці зібрали 8 кг огірків, що становить зібраних овочів. Скільки кілограмів овочів зібрали?

485. На присадибній ділянці зібрали 8 кг огірків, що становить 0,4 зібраних овочів. Скільки кілограмів овочів зібрали?

486. На присадибній ділянці зібрали 8 кг огірків, що становить 40% зібраних овочів. Скільки кілограмів овочів зібрали?

Рівень А

487. Який шлях пройде група туристів за 1 год, якщо  км вона проходить за  год;  год;  год?

Площа прямокутника дорівнює  м2. Знайдіть його ширину, якщо довжина дорівнює  м;  м.

489. За  м тканини заплатили 183 грн. 75 коп. Яка ціна одного метра тканини?

Автомат розфасовує желатин у пакетики по 0,03 кг. Скільки пакетиків потрібно для розфасування кг желатину?

491. Довжина земельної ділянки прямокутної форми дорівнює 40 м, а ширина — в  разу менша. Знайдіть площу ділянки.

492. Перша сторона трикутника дорівнює  м, друга i третя — відповідно в й разу коротші від першої. Знайдіть периметр трикутника.

Знайдіть число:

493. а) якого дорівнює 21; б) якого дорівнює 30;

в) 0,7 якого дорівнює 14; г) 0,21 якого дорівнює 0,609.

а) якого дорівнює 25; б) якого дорівнює ;

в) 0,45 якого дорівнює 3,6; г) 0,18 якого дорівнює 0,342.

495. Кукурудзою засіяли 78 га поля, що становить площі всього поля. Яка площа всього поля? Нарисуйте схему для розв’язання задачі.

Український транспортний літак АН-225 («Мрія») увійшов до Книги рекордів Гіннеса, піднявши в повітря вантаж масою 250 т. Ця маса становить маси літака з вантажем. Якою була маса завантаженого літака. Нарисуйте схему для розв’язання задачі.

497. Фабрика, одержавши замовлення, виготовила 120 столів, що становить необхідної кількості. Скільки столів залишилося виготовити, щоб виконати замовлення?

498. Цукор-пісок у процесі переробки на рафінад втрачає своєї маси. Скільки потрібно взяти цукру-піску, щоб одержати 52 ц рафінаду?

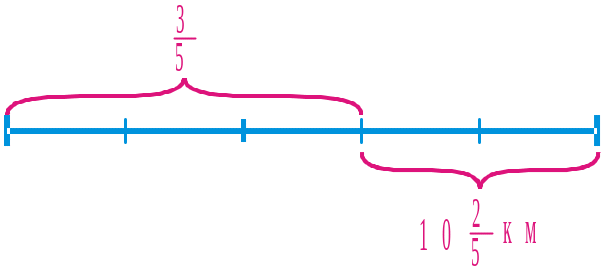
Після того як туристи пройшли запланованого шляху, їм залишилося пройти ще  км. Знайдіть запланований шлях.

Скористайтеся схемою:

Знайдіть число:

500. а) 15% якого дорівнює 36; б) % якого дорівнює 41.

а) 35% якого дорівнює 7; б) % якого дорівнює 1,5.

502. Із жита отримують 75% борошна. Скільки жита потрібно змолоти, щоб отримати 60 кг борошна? Нарисуйте схему для розв’язання задачі.

У класі 3 відмінники, що становить 12% усіх учнів класу. Скільки учнів у класі? Нарисуйте схему для розв’язання задачі.

504. Ширина пасовища прямокутної форми дорівнює 30 м, що становить 48% довжини. Яка площа пасовища?

505. У парку першого дня посадили 96 дерев. Це становить відповідно 80% i 75% кількості дерев, посаджених другого і третього дня. Скільки дерев посадили за три дні?

506. Складіть задачу за її розв’язанням:

1) 25% = 0,25; 2) 5 : 0,25 = 20 (кг).

Рівень Б

507. Постамент із граніту має форму прямокутного паралелепіпеда. Його ширина дорівнює  м, що становить довжини і 37,5% висоти. Знайдіть масу постаменту, якщо 1 м³ граніту має масу 2,7 т.

508. Дорога до міста складається з підйомів, спусків та горизонтальних ділянок. Підйоми становлять 30% усього шляху, спуски  70% підйомів, а решта 24,5 км  горизонтальні ділянки. Знайдіть довжину дороги.

До магазину завезли яблука, груші й сливи. Маса яблук становить 60% завезених фруктів, маса груш  25%, а решта — 45 кг  сливи. Скільки кілограмів яблук і груш окремо завезли до магазину?

510. Дві снігоприбиральні машини можуть прибрати сніг з ділянки вулиці за 6 год. Після 3 год спільної роботи першу машину направили в інший район міста, а друга закінчила роботу за 5 год. За скільки годин кожна машина, працюючи окремо, може виконати всю роботу?

Для вирівнювання дороги використали дві грейдерні машини різної потужності. Одна з них може виконати деяку роботу за 20 год, а інша — за 30 год. За який час дві грейдерні машини можуть виконати роботу, працюючи разом?

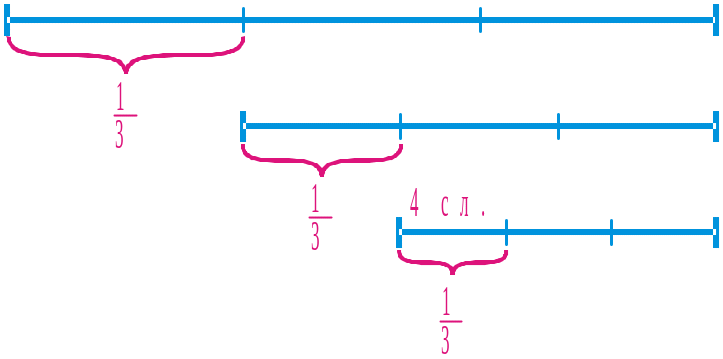
512. Мама залишила для трьох синів тарілку слив, а сама пішла на роботу. Першим зі школи прийшов молодший син, він побачив на тарілці сливи, з’їв третю частину і пішов гуляти. Другим прийшов середній син. Подумавши, що його брати ще не ласували сливами, він з’їв третю частину тих, що були на тарілці, й теж пішов гуляти. Останнім прийшов старший син і з’їв 4 сливи — третю частину тих, що були на тарілці. Скільки слив було на тарілці спочатку?

Скористайтеся схемою:

513. З повної чашки я відпив спочатку чашки кави і долив стільки ж молока, потім відпив ще чашки кави з молоком і знову долив стільки ж молока, після чого відпив ще чашки кави з молоком. Яку частину чашки кави з молоком, що залишилася, становить кава?

Розв’язання

	Відпив кави	Залишилося кави у чашці
1.	вмісту чашки	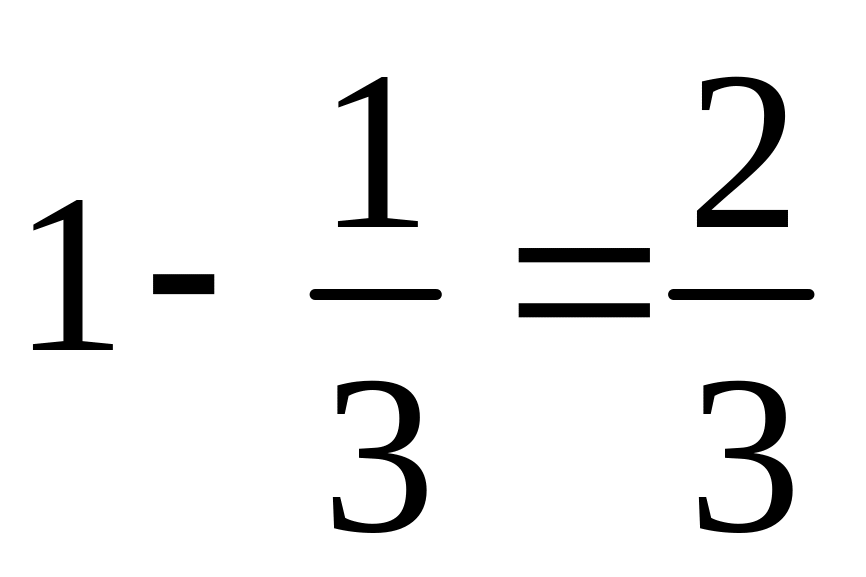вмісту чашки
2.	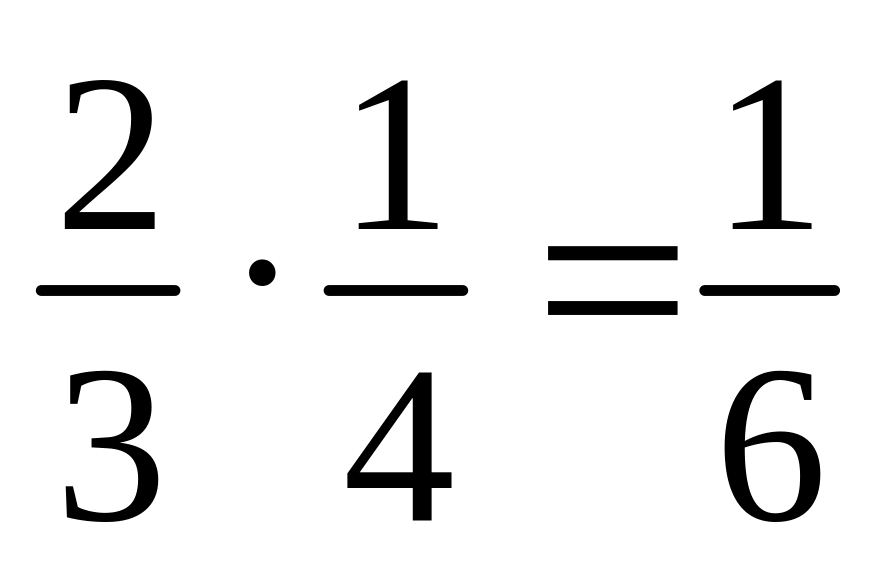вмісту чашки	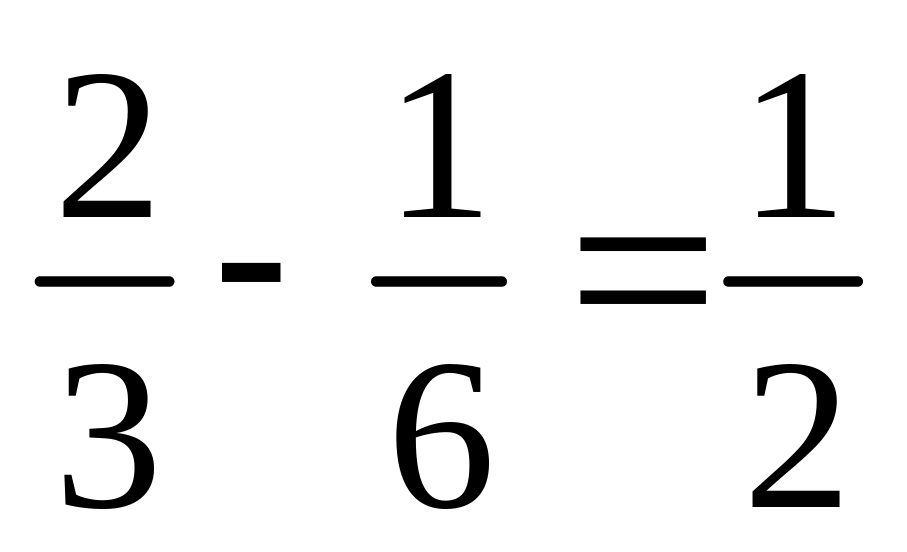вмісту чашки
3.	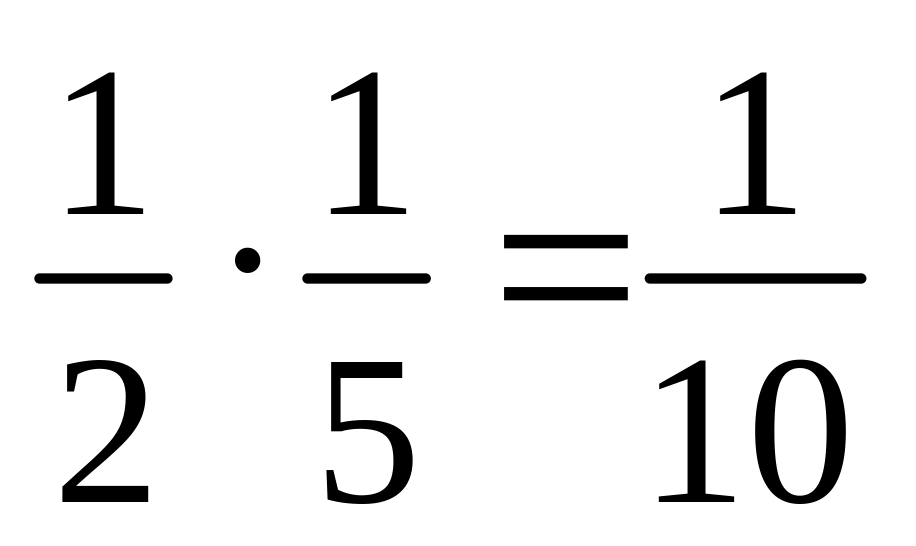вмісту чашки	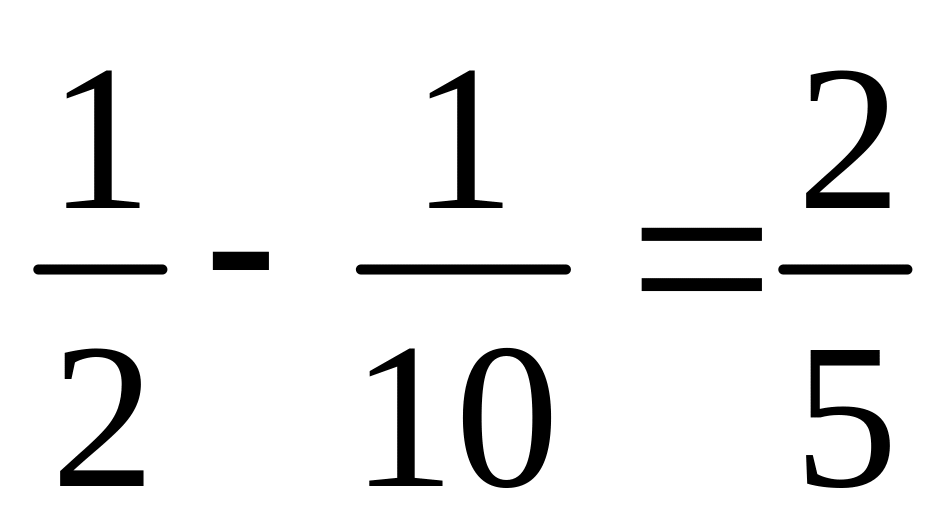вмісту чашки

Відповідь.  вмісту чашки.

514*. Свіжі гриби містять 90% води, а сушені  12%. Скільки кілограмів сушених грибів вийде із 22 кг свіжих?

Розв’язання

1) 100%  90% = 10%  становить суха маса у свіжих грибах.

2) 10% = 0,1;   22  0,1 = 2,2 (кг)  становить суха маса у 22 кг свіжих грибів.

3) 100%  12% = 88%  становить суха маса у сушених грибах.

4) 88% = 0,88;   2,2 : 0,88 = 2,5 (кг)  маса сушених грибів.

Відповідь. 2,5 кг.

Вологість трави становить 80%, а сіна  20%. Скільки вийде сіна з 1 т трави?

516*. Зрубали дерево масою 5 ц, деревина якого мала вологість 64% (тобто деревина містила 64% води). Через тиждень вологість становила вже 55%. На скільки центнерів зменшилась маса дерева за тиждень?

Здогадайтеся

517. З повної чашки кави я відпив половину і долив стільки ж молока. Потім я відпив третю частину кави з молоком і долив стільки ж молока. Потім я відпив шосту частину кави з молоком і долив стільки ж молока. Після цього я випив усю каву з молоком. Чого в результаті я випив більше — кави чи молока?

Вправи для повторення

Знайдіть значення виразу:

518. а) 8,45 · 9,6 – 7,8 · 8,45; б) 37,5 + (62,8 – 27,5) : 4.

519. а) 31,2 : x + 6,7, якщо x = 10; б) 38,5 + a : b, якщо a = 19,8; b = 90.

520. Сергій почав бігти за Андрієм, коли між ними була відстань 180 м. Через який час Сергій наздожене Андрія, якщо швидкість Сергія дорівнює 12 км/год, а швидкість Андрія — 9 км/год?

521. Точка K належить відрізку MN. Довжина відрізка MK дорівнює 3 см 5 мм, а відрізок KN на 7 мм довший. У скільки разів відрізок MN довший за відрізок МK?

522. Довжина прямокутного поля 860 м, а ширина — на 360 м менша. Знайдіть площу поля та запишіть її в гектарах i арах.

523. Скількома способами можна розкласти у дві кишені чотири монети номіналом 5 к., 10 к., 25 к., 50 к.?