1.2. Метод амперметра и вольтметра

М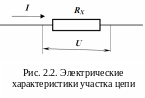 ожно измерить электрическое сопротивление и косвенно, используя закон Ома , где R_Х – сопротивление проводника, U – напряжение, приложенное к его концам, I – сила тока в проводнике (рис. 2.2). Необходимые значения напряжения и силы тока получают с помощью вольтметра и амперметра. Однако невозможно собрать такую схему подсоединений этих приборов к измеряемому сопротивлению, в которой бы вольтметр измерял напряжение U, а амперметр в это же время – силу тока I.

С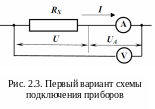 уществует два варианта схемы подсоединений. В первом (рис. 2.3) из них амперметр измеряет силу тока I, протекающего через сопротивление, а вольтметр ― сумму напряжений на амперметре U_A и сопротивлении U.

Во втором варианте схемы (рис. 2.4) вольтметр измеряет напряжение на сопротивлении U, а амперметр ― сумму сил токов, протекающих по сопротивлению I и по вольтметру I_V : .

Е сли внутренние сопротивления вольтметра и амперметра известны, то с помощью законов Ома и Кирхгофа по результатам измерений можно вычислить значение искомого сопротивления.

Рассмотрим, как выполняется такой расчёт в первом варианте схемы. Обозначим отношение показания вольтметра U_V к показанию амперметра через R₁.

. (2.1)

Очевидно, что R₁ = R_А + R_X, а искомое сопротивление

R_X = R₁  – R_А. (2.2)

Если же нам неизвестно значение сопротивления амперметра, и в качестве результата измерений мы принимаем R₁, то мы завышаем истинное значение сопротивления на величину R_А, которая является систематической абсолютной погрешностью измерений порождаемой особенностями первого варианта схемы. Относительная погрешность при этом будет

.

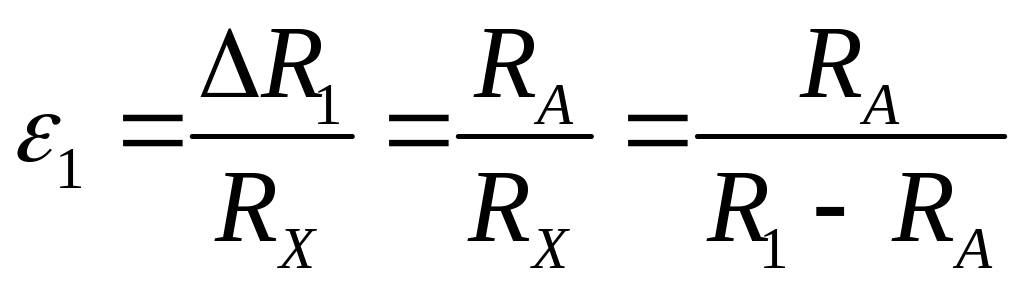Рассмотрим расчёт значения искомого сопротивления R_X во втором варианте схемы. По закону Ома 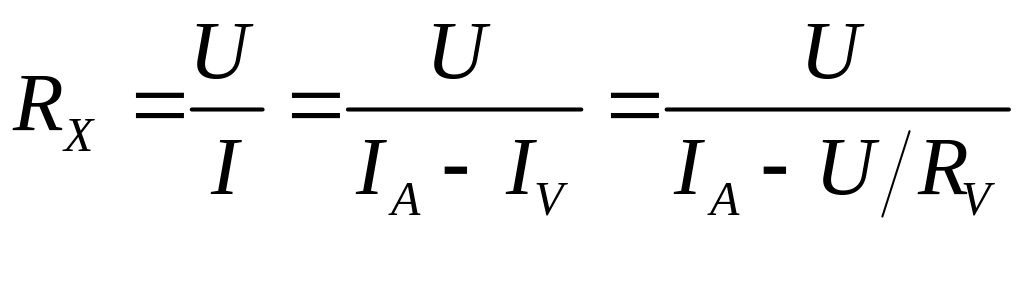. Обозначим через R₂ отношение показания вольтметра к показанию амперметра:

. (2.3)

Очевидно, что 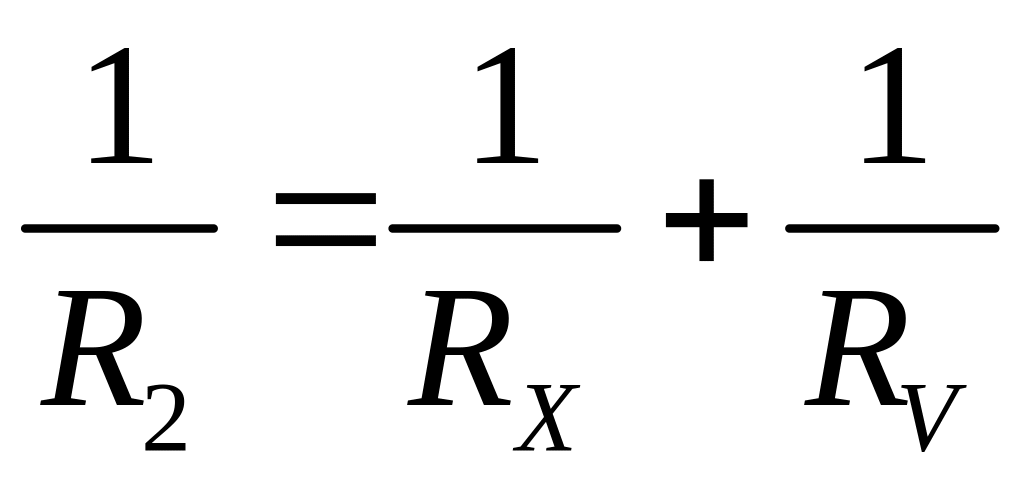, а искомое сопротивление

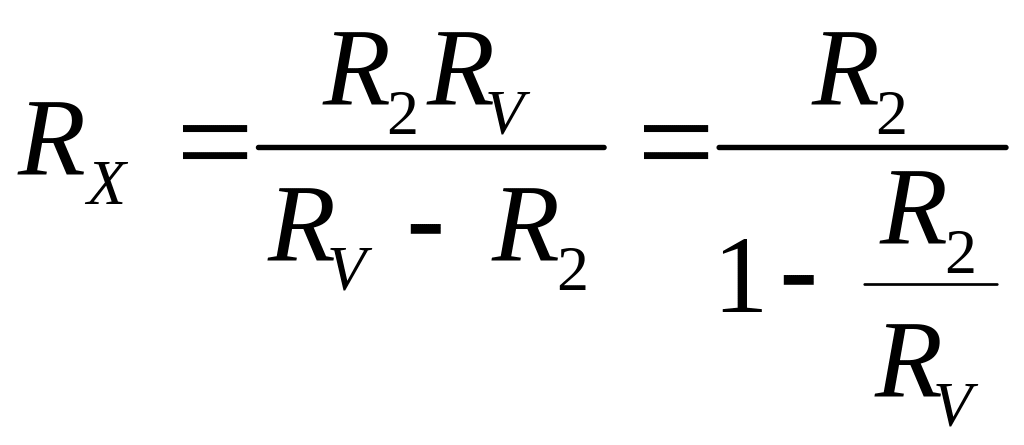. (2.4)

Если значение R_V неизвестно, и в качестве результата измерения принять R₂, то будет допущена систематическая (связанная с особенностями этой схемы) погрешность, занижающая значение измеряемого сопротивления. Модуль абсолютной систематической погрешности

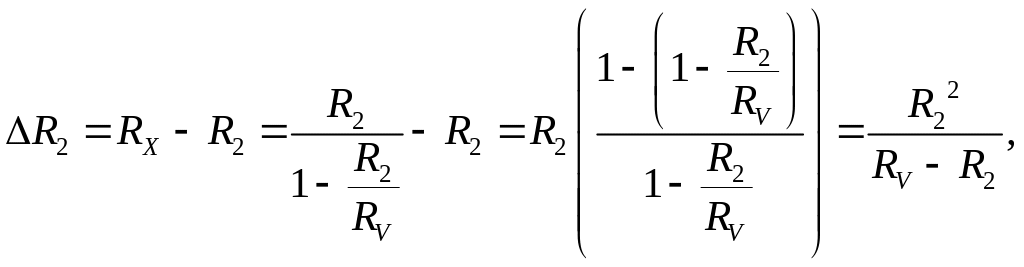
а модуль относительной систематической погрешности для второго варианта схемы

(выведите это самостоятельно!).

Таким образом, показали, что оба варианта схемы позволяют узнать величину измеряемого сопротивления, если известны значения внутреннего сопротивления амперметра (для первого варианта, формула (2.2.)) или вольтметра (для второго варианта, формула (2.4)).

Если значения внутренних сопротивлений приборов неизвестны, то приближённые значения измеряемого сопротивления содержат систематические погрешности, обусловленные схемами подключений приборов. Причём в первом варианте относительная погрешность уменьшается с возрастанием величины измеряемого сопротивления, а во втором ― увеличивается. Можно вывести, при каком измеряемом сопротивлении эти погрешности станут равными. Хорошим приближением к этому значению является . (Предлагаем получить это значение, учитывая то, что R_A << R_V, самостоятельно!). Следовательно, в случае приближённых измерений сопротивлений следует использовать первую схему, а иначе – вторую.