Билет №12
Объединение случайных совместных событий. Вычисление вероятности и пример применения.
Радиолампа поступила с одного из трех заводов с вероятностями 0,35; 0,45; 0,2 соответственно. Вероятность выхода из порядка на протяжении года равняется 0,2 для ламп изготовленных первым заводом, 0,3 - для ламп изготовленных вторым заводом и 0,1 - третьим. Найти вероятность, что лампа успешно проработала год.
Вероятность того, что в коробке будет бракованная деталь 0,4. Найти вероятность того, что среди 8 деталей будет две бракованные.
Билет №13
Формула полной вероятности. Пример применения.
К группе спортсменов входит 10 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнения нормы разряда для лыжника составляет 0,8, для велосипедиста - 0,75, для бегуна - 0,7. Выбранный наугад спортсмен выполнил норму разряда. Найти вероятность, что он лыжник.
Случайная величина х задана функцией распределения
.
Найти: а) плотность распределения случайной величины Х;
б) математическое ожидание, дисперсию, среднее квадратическое отклонение;
в)
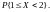
Билет №14
Переоценка гипотез. Формула Байеса.
Вероятность того, что студент сдаст зачет с первого раза равняется 0,3. Найти вероятность того, что среди 10 студентов ровно 4 сдадут зачет с первого раза.
Два спортсмена независимо друг от друга делают по одном выстрелу в мишень. Вероятность попадания для первого равняется 0,7, а второго - 0,8. Найти вероятность таких событий:
а) A – оба попали в мишень;
б) C – ни один из спортсменов не попал в мишень;
в) D – хотя бы один спортсмен попал в мишень.
Билет №15
Последовательность испытаний. Схема и формула Бернулли.
В двух коробках лежат черные и белые шары. В первой коробке три белых и один черный; во второй - 6 белых и 4 черных. Наугад выбирают коробку, а из нее вынимают один шар. Найти вероятность того, что извлеченный шар есть белым.
Задан закон распределения случайной величины х
X |
-2 |
-1 |
0 |
1 |
P |
0,1 |
0,4 |
0,2 |
0,3 |
Нужно: а) построить многоугольник распределения ДВВ Х;
б) найти математическое ожидание, дисперсию и среднее квадратическое отлонение Х;
в)
Билет №16
Следствия формулы Бернулли в схеме Бернулли.
К группе спортсменов входит 10 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнения нормы разряда для лыжника составляет 0,8, для велосипедиста - 0,7, для бегуна - 0,6. Выбранный наугад спортсмен выполнил норму разряда. Найти вероятность, что он бегун.
Вероятность того что событие A состоится в каждом с 10 независимых испытаний равняется 0,7. Найти вероятность того, что событие A состоится хотя бы один раз.
Билет №17
Дискретные случайные величины и способы их задання.