Срс 7 по дисциплине “Теория распределение информации»

Наименование темы: Коэффициент использования линии (сервера), единичное приращение интенсивности обслуженной нагрузки

На рис. 1. приведены результаты расчета коэффициента использования линии (сервера):

.

В предположении ИСС для различных значений g, D=10, p_B=0.003.

Характерно, что с ростом числа серверов использование линии сначала увеличивается, а затем уменьшается. В крайних точках m=g и m=gD использование линии одинаково, так как соответствует полнодоступному включению.

Рис. 1. Среднее использование линии  в НВ в зависимости от емкости пучка m при различных значениях g, D=10 и P=0.003.

Важной практической характеристикой СМО с несколькими серверами является единичное приращение интенсивности обслуженной нагрузки при увеличении числа серверов на единицу и постоянной норме потерь - вероятности блокировки. Эту величину называют единичным приращением

.

Для полнодоступных систем при постоянной вероятности блокировки и постоянном числе входных линий из полученных ранее формул для обслуженной нагрузки следуют неравенства:

Это неравенство говорит о том, что удвоение числа серверов увеличивает пропускную способность системы более чем вдвое. Рис. 2 показывает зависимость единичного приращения от числа серверов в полнодоступной системе при фиксированной вероятности блокировки. Для неполнодоступных систем рост единичного приращения от числа серверов заметно меньше, чем для полнодоступной.

Рис. 2 Зависимость единичного приращения y_ от числа выходов m при обслуживании простейшего потока и различных вероятностях потерь Р_В.

При переходе от схемы ПВ к схеме НВ значение единичного приращения скачкообразно уменьшается.

Эскизные расчеты схем НВ могут проводиться с помощью приближенных формул. Формула О’Делла, позволяющая оценить необходимое число серверов m при неполнодоступной схеме их включения с доступностью D по заданной обслуженной нагрузке Y и вероятности блокировки:

.

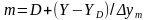Здесь используется базовая величина для обслуженной нагрузки D серверами.

Коэффициент использования сервера при γ =1:

.

С ростом γ, величина единичного приращения увеличивается, как было пока­зано, для ИСС можно считать .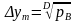

Пусть на некоторую ИСС поступает γ пуассоновских потоков интенсивностью b=λ/gD каждый. С ростом m число потоков:

Вероятность занятия одного фиксированного сервера тогда может быть задана величиной в точности равной η=Y/m . Для D фиксированных серверов эта вероятность будет очевидно η^D . Для схем НВ эта вероятность в точности равна p_B. Следовательно, приходим к соотношениям

В некоторых странах принято использовать формулу Пальма -Якобеуса для определения обслуженной нагрузки и вероятности блокировки. Она представляет собой систему нелинейных уравнений следующего вида

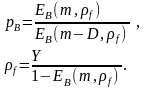
Здесь используется функция Эрланга, определенная ранее.