Срс 5 по дисциплине “Теория распределение информации»

Наименование темы: Система обслуживания M/M/m:K/M конечное число источников нагрузки, m серверов и конечный накопитель

О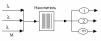 сновной смысл изучения такой системы состоит в том, что входной поток в такой системе может рассматриваться как примитивный, то есть параметр потока зависит от числа требований, находящихся на обслуживании. Эта зависимость определяется таким образом, что из M источников пуассоновского потока с постоянным параметром λ получают отказ те требования, которые поступают в систему тогда, когда в ней уже имеются K заявок. Система описывается процессом типа гибели-размножения с диаграммой интенсивностей переходов на рис. 1.

Рис. 1. Диаграммой интенсивностей переходов для СМО типа M/M/m:K/М.

и параметрами интенсивностей:

Воспользовавшись формулам для стационарных вероятностей, получим:

Формула для вероятности простоя очень громоздка и здесь не приводится. Если считать, что K = m , то есть в системе только чистые потери (длина буфера совпадает с числом серверов), то распределение стационарных вероятностей может быть дано в виде так называемого распределения Энгсета:

Эта формула имеет следующую интерпретацию.

Н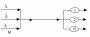 екоторая система массового об­служивания, имеющая М входных линий, распределяет поступающие с них заявки на m серверов. Интен­сивность входного потока зависит от того, сколько серверов занято об­служиванием таким образом, что интенсивность входного потока ли­нейно убывает с числом занятых серверов : .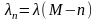

Максимальная нагрузка, поступающая на один вход, определяется как: .

Вероятность того, что при показательном законе распределения времени обслуживания в стационарном режиме будет занято k серверов, будет определяться как раз вышеприведенной формулой Энгсета. Систему такого типа можно назвать M/M/m:M. Полученное распределение также позволяет рассчитать вероятность того, что будут заняты все серверы. Для этого достаточно положить k = m . Как видно, она отличается от полученной ранее формулы потерь Эрланга. Это распределение также часто встречается на практике и задается функцией Энгсета: .

На практике применима также модель Молина (Molina), которая также называется моделью потерянных вызовов (LCH – Lost Calls Held). Это математическая модель блокировки телефонного трафика, в которой блокированные обращения сохраняются в течение определенного времени задержки, хотя и не обслуживаются. Эта модель подобна модели, описываемой С – формулой Эрланга, с которой иногда и путается. Вероятность блокировки для N линий, создающих интенсивность А имеет вид:

.

Срс 6 по дисциплине “Теория распределение информации»

Наименование темы: Анализ систем связи

Рассмотрим узел коммутации каналов. На практике это может быть транзитная АТС, которая коммутирует соединительные линии разных направлений, оконечная АТС, входные линии которой являются как соединительными, так и абонентскими. Это может быть также учрежденческая АТС или выносной концентратор городской станции.

Будем полагать, что коммутатор имеет M входящих и m исходящих линий.

Опишем поток заявок следующими параметрами. Пусть каждый абонент в среднем делает 1 звонок каждые 30 минут, занимая линию в среднем на 3 минуты.

Пусть общее число абонентов М=120. Основной задачей при проектировании является определение числа исходящих линий, достаточного, для обеспечения заданного уровня качества обслуживания. Важнейшей характеристикой качества является вероятность блокировки по времени.

Одним из подходов к анализу является применение модели Эрланга .

Будем рассматривать все вызовы, поступающие от абонентов как общий Пуассоновский поток с параметром: вызовов в минуту.

Найдем нагрузку: Эрлангов

Воспользуясь В-формулой Эрланга, можно найти следующие значения вероятностей блокировки при различном числе выходных линий:

PB,%	m	/m
1	20	0.6
4	17	0.7
8	15	0.8
19	12	1.0
30	7	1.7

При умеренных нагрузках (5<ρ<50), можно использовать приближенные формулы:

Другим подходом является использование модели Энгсета. При этом вероятность блокировки по времени можно рассчитать как значение: .

Найдем несколько значений этой функции.

pB,%	m	Mρ/m
1	18	0.7
4	16	0.75
8	14	0.86
19	11	1.1
30	9	1.3

Как можно видеть из таблиц, приведенных выше, применение моделей Эрланга и Энгсета несущественно при рассмотрении небольшой удельной нагрузке на сервер, расхождения заметны лишь для больших удельных потенциальных нагрузках. Обычно на практике рассматриваются пучки исходящих каналов и вызовы на каждый из пучков считают Пуассоновскими потоками. К каждому пучку применимо распределение Эрланга. Вероятности состояния каждого из исходящих пучков более приемлемо при этом описывать распределением Энгсета.