9. Окружность. Хорды и углы.

Докажем сначала несколько теорем, достаточно часто применяемых при решении различных задач.

77. (!) Доказать, что две дуги окружности, заключен­ные между двумя параллельными ее хордами, равны меж­ду собой..

Справедливость этого достаточно очевидного утверж­дения следует из симметрии окружности относительно

любого ее диаметра (рис. 19). При симметрии относительно диаметра, перпендикулярного параллельным хордам АВ и CD, дуги АС и BD совместят­ся).

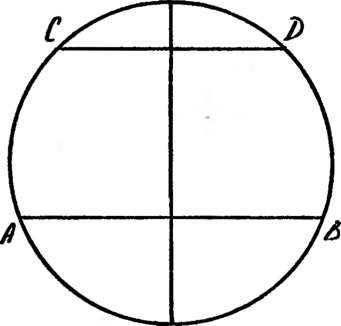
Рис. 19

и В, продолжения этих в точках А\ и В\. Нам измеряется полусуммой /LAMB равен полусумме центральных углов, соответству­ющих дугам АВ и AiBi. Мы знаем, что вписанный в окружность угол измеряется половиной дуги, на которую он опирается. Рассмотрим Д МА\В. Угол АМВ является внешним углом этого Д: ЛАМВ= Z.MA\B-\- + Z.MBA\ = Z.AA\B-{- Z.B\BA\. В последнюю сумму вхо­дят вписанные углы, измеряемые полусуммой дуг АВ и AiBi. Наше утверждение доказано.

89. (!) Доказать, что угол с вершиной внутри круга изме­ряется полусуммой дуг, заклю­ченных между его сторонами и продолжением его сторон за вершину угла. На рис. 20 сто­роны угла с вершиной М пере­секают окружность в точках А сторон пересекают окружность надо доказать, что угол АМВ дуг АВ и А\В\, то есть, что

Докажите самостоятельно, что

90. (!) Угол с вершиной вне круга измеряется полураз­ностью дуг, заключенных меж­ду сторонами угла. (Предпола­гается, что каждая из сторон пересекается с данной окруж­ностью).

Проведем через точку М, расположенную внутри круга, две хорды АВ и CD (рис.21). Тогда треугольники AMD и СМВ подобны (также подо­

бны и треугольники АМС и DMB), равные углы одинаково отмечены на рис.21 (Этот факт стоит за­помнить.) Значит, откуда AM-BM=CM-DM,

л

Рис. 20

j)

Рис. 21

Рис. 22

проведем через М диаметр, то отрезки этого диаметра будут R+а и R —а, где R — радиус окружности, а — рас­стояние М от центра окружности. Произведение отрезков диаметра равно R²—a . Таким образом, мы доказали теорему.

91. (!) Пусть М — точка внутри окружности радиуса R, расположенная на расстоянии а от центра окружности, АВ — произвольная хорда, проходящая через М. Тогда AM-BM—R²—cP. Из школьного учебника мы знаем, что у вписанного четырехугольника сумма противоположных углов равна 180°. (Это следует из того, что сумма проти-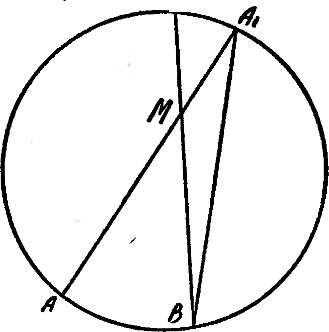

т. е. произведение отрезков хорды, проходящей через М, на которые хорда делится точкой М, постоянно. Если мы

воположных углов вписанного четырехугольника измеря­ется половиной целой окружности). Верно и обратное утверждение.

92. (!) Если сумма противоположных углов четырех­угольника равна 180°, то этот четырехугольник вписан­ный.

Доказательство. Пусть в четырехугольнике ABCD сум­мы противоположных углов равны 180°. Опишем около треугольника ABC окружность. Допустим, что точка D не лежит на этой окружности. Обозначим через D\ точку пересечения этой окружности с прямой AD (рис. 22). Тогда углы AD\C и ADC равны между собой, поскольку каждый из них дополняет до 180° угол ABC. Получаем, что в треугольнике CDD\ внешний угол равен внутренне­му, с ним несмежному, что невозможно. Значит, точки D и D\ совпадают.

Аналогично доказывается также, что

92. (!) Если в четырехугольнике ABCD равны углы ABD и ACD, то этот четырехугольник вписанный.

93. В треугольнике ABC угол А равен 32°, угол С равен 24°. Окружность с центром в точке В проходит через Л, пересекает АС в точке М, ВС — в точке N. Чему равен угол ANM?

Ответ: (58°)

92. В треугольнике ABC известны стороны АВ—2, ВС—4, С А—3. Окружность, проходящая через точки В и С, пересекает прямую АС в точке М, а прямую АВ в точке N. Известно, что AM — 1, СМ =4 Найти NM и AN.

Ответ: ( 2,

92. Диагонали четырехугольника ABCD, вписанного в окружность, пересекаются в точке М, прямые АВ и CD пересекаются в точке N. Известно, что ЛЛАШ = 108°, Z.AND=24°. Найти /LABD и ABDC.

Ответ: (66°, 42°)

92. Около треугольника со сторонами 5, 6 и 7 описана окружность. Найти длину хорды этой окружности, отлич­ной от стороны треугольника, проходящей через одну его вершину и делящей пополам среднюю по длине сторону треугольника.

Ответ: (

92. В четырехугольнике ABCD известны углы Z.ADC=96°, ЛВАС=54°, ААСВ=42°. Чему равен Z.BDC?

Ответ: (54°)

92. Пусть М — точка На диаметре АВ окружности с центром в О. С и D — точки окружности, расположен­ные по одну сторону от А В, причем Z.CMA — Z.DMB, ACMD — a. Чему равен угол COD?

Ответ: (а)

92. Пусть АВ диаметр окружности, С—некоторая точка плоскости. Прямые АС и ВС вторично пересекают окружность в точках М и N соответственно. Прямые MB и NA пересекаются в точке К. Чему равен угол между прямыми СК и АВ?

Ответ: (90°)

10. Окружности и касательные. Площадь круга и его частей.

Сформулируем и докажем сначала две теоремы. Пер­вая из них продолжает тему задач №№ 89, 90, являясь в известном смысле их частным, а вернее, предельным случаем.

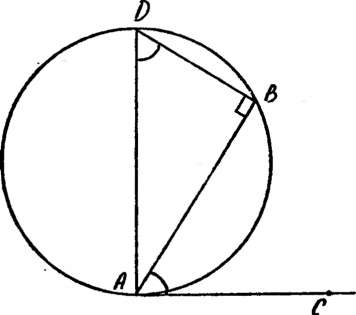
92. (!) Проведем через некоторую точку окружности хорду и касательную к окружности. Тогда каждый из двух углов, образованных этими хордой и касательной, измеря­ется половиной дуги, заклю­ченной внутри соответствую­щего угла.

Доказательство. Пусть АВ — хорда окружности, АС — касательная, AD — диаметп^ис. 23). АВАС = = ZJBDA, поскольку каж­дый из этих углов допол­няет до 90° угол BAD. Сле­довательно, угол ВАС, как р_ис 23 ^и вписанный угол BDA,. из­

меряется половиной дуги АВ, заключенной внутри угла ВАС.

Следующая теорема 102 по формулировке и доказа­тельству аналогична теореме 91.

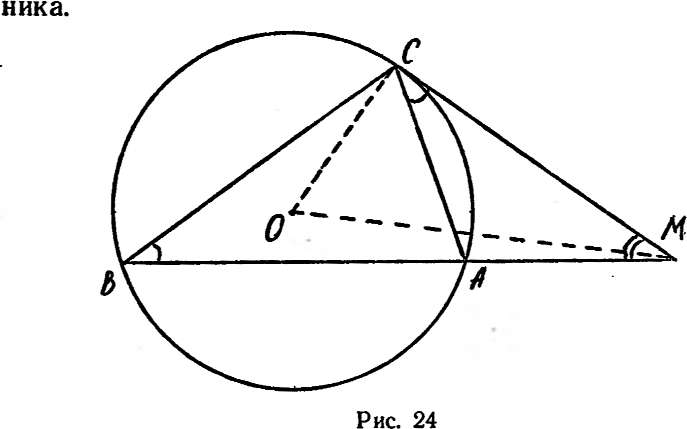
92. (!) Пусть М — точка, расположенная вне окруж­ности радиуса R, на расстоянии а от ее центра. Произ­вольная секущая, проходящая через М, пересекает ок­ружность в точках А и В, МС — касательная к окружно­сти (С — точка касания). Тогда

МА-МВ=МС²=а²—R².

Доказательство. Утверждение следует из подобия тре­угольников МСА и МВС (равенство углов МСА и МВС

следует из теоремы 101, рис. 24). Имеем

Откуда MA'MB=MC² = a²—R². Последнее равенство получено из треугольника МОС на основании теоремы Пифагора.

Аналогом теоремы 92 для вписанного четырехугольни­ка является теорема 103 для описанного четырехуголь-

103. (!) Если ABCD — описанный около некоторой окружности четырехугольник, то AB-\-CD=BC+DA.

Обратно, если для выпуклого четырехугольника вы­полняется равенство АВ + CD=ВС+DA, то в этот четы рехугольник можно вписать окружность.

Первая часть нашего утверждения следует из равен­ства касательных, проведенных к окружности из одной точки. Пусть касательные к окружности, вписанной в ABCD, проведенные соответственно из вершин А, В, С и D, равны а,Ь,с и d (рис. 25а). Тогда АВ + С£> = а+6+с-М, BC+DA=b + c+d+a, то есть АВ + CD = BC-\-DA.

Обратное утверждение, как обычно, доказывается от противного. Проведем биссектрисы углов А и D четырех­угольника ABCD и обозначим через О точку их пересече­ния (рис. 256). Точка О равноудалена от сторон АВ и AD, а также от сторон AD и DC, и мы можем построить окружность с центром О, касающуюся этих сторон. Пусть суммы противоположных сторон четырехугольника ABCD равны, но построенная окружность не касается стороны ВС. Проведем через С касательную к окружности, отлич­ную от CD, и обозначим через В\ точку пересечения этой касательной с прямой АВ. Четырехугольник AB\CD явля­

ется описанным, следовательно AB\ + CD=B\C+DA. По усло­вию AB-\-CD=BC-\-DA. Вычи­тая друг из друга эти два ра­венства, получим BBi — \BC— —В\С\, то есть в треугольнике СВВ\ разность двух сторон равна третьей стороне. Это невозмож­но. Значит, точки В и В\ должны совпадать.

Замечание. Можно предло­жить и иное, прямое рассуждение. Отложим на AD отрезок АМ=АВ (для удобства полагаем AD> АВ), а на

CD отложим С К—ВС (рис. 25в). Из равенства AB + CD = AD + BC следует, что MD — AD—AB = CD — — BC=KD. Теперь биссектрисы углов А, С и D нашего четырехугольника будут срединными перпендикулярами к сторонам треугольника ВМК, значит, они пересекаются в одной точке — центре описанной около ВМК окружнос­ти. Точка эта, как легко видеть, равноудалена ото всех сторон четырехугольника ABCD.

В заключение этого раздела напомним формулы, вы­ражающие длину дуги окружности, а также площади круга и его частей.

Длина окружности L = 2nr. Длина дуги, которой соот­ветствует центральный угол величины а (в радйанной мере), вычисляется по формуле /=;га. Площадь круга:

Рис. 25а

лг², площадь сектора S=-|-r²a, площадь сегмента, соот­ветствующего дуге (центральному углу) лучше всего представить в виде разности площадей-еектора и равно­

бедренного треугольника с боковыми сторонами, равными г и углом между ними а. Значит 5_сегм=-|-г²(а —sin а)

Напомним примечание, сделанное в свое время к зада­че № 62. Площадь любого описанного многоугольника в частности четырехугольника, можно находить по форму­ле s=pr, где р — его полупериметр, г — радиус вписан­ной окружности.

104. Около окружности описана равнобочная трапе­ция с основаниями 5 и 3. Найти радиус окружности.

Ответ: ^ -^yJlE^j

104. Из точки, расположенной вне окружности, прове­дены касательная и секущая. Длина касательной равна 6. Секущая высекает на окружности хорду длиной 5. Найти длину отрезка секущей, расположенного вне окружности.

Ответ: (4)

104. Через вершины В и С треугольника ABC прохо­дит окружность, пересекающая стороны АВ и АС соот­ветственно в точках К и М. Доказать, что треугольники ABC и АМК подобны. Найти МК и AM, если АВ=2, ВС=4, СА=5, АК=\. _{/4 2Ч}

Ответ:

104. Окружность высекает на сторонах четырехуголь­ника равные хорды. Доказать, что в этот четырехугольник можно вписать окружность.

105. Около окружности радиуса 1 описана равнобоч­ная трапеция с боковой стороной, равной 3. Найти пло­щадь трапеции.

Ответ: (6)

104. Около окружности описана трапеция. Доказать, что концы боковой стороны трапеции и центр окружности являются вершинами прямоугольного треугольника. До­казать, что произведение отрезков боковой стороны, на которые она разделена точкой касания, равно квадрату радиуса окружности.

105. К окружности проведены касательные, касаю­щиеся ее в концах диаметра АВ. Произвольная касатель­ная к окружности пересекает эти касательные соответст­венно в точках К и М (АК и ВМ — касательные к окружности). Доказать, что произведение АК'ВМ по­стоянно.

106. 33

     На сторонах АВ и АС квадрата ABCD взяты точки К и М так, что ЗАК—4АМ—АВ. Доказать, что прямая КМ касается окружности, вписанной в квадрат.

31-921

104. Дан прямоугольный треугольник с гипотенузой 2 и острым углом 30°. Найти площадь общей части двух кругов, проходящих через вершину прямого угла с цент­рами в вершинах острых углов треугольника.

Ответ: л/з)

104. На катетах прямоугольного треугольника, как на диаметрах построены круги. Доказать, что сумма площа­дей частей этих кругов, расположенных вне описанного около треугольника круга, равна площади треугольника.

СТЕРЕОМЕТРИЯ.