Построение кратчайших путей на графе
3.1. Алгоритм Дейкстры и алгоритм Форда
Алгоритм Дейкстры позволяет построить на взвешенном ориентированном графе путь минимального веса (кратчайший) между двумя выделенными вершинами.
Условимся обозначать через s и f соответственно начало и конец пути. При работе алгоритма некоторые дуги и вершины будут выделяться - окрашиваться. Вершине vi с произвольным номером i присваиваются две метки: l(i) - длина кратчайшего пути из вершины s в вершину vi, включающего только окрашенные вершины; θ(i) - номер предпоследней вершины в этом пути. Номер последней по порядку окрашенной вершины обозначим через p.
Алгоритм Дейкстры реализуется как последовательность следующих шагов:
Положить l(s)=0 и l(i)=∞ для всех vi≠s. Окрасить s и положить p=s.
Для всех неокрашенных вершин выполнить проверку:
если l(p)+w(p,i)<l(i), то l(i)=l(p)+w(p,i) и θ(i)=p.
Если теперь для всех неокрашенных вершин l(i)=∞, то перейти к шагу 5, так как из s нет путей в неокрашенные вершины. Иначе окрасить вершину с наименьшей меткой l(k) и дугу (θ(k),k); перейти к шагу 4.
Если p=f, то перейти к шагу 5, иначе перейти к шагу 2.
Закончить выполнение алгоритма.
Просматривая по окончании работы алгоритма метки θ(f)=k1,θ(k1)=k2,…, θ(kj)=s, восстанавливаем в обратной последовательности путь s … f.
Алгоритм применим к неориентированным графам. Каждое ребро рассматривается как пара дуг, которые имеют тот же вес, что само ребро.
Если модифицировать п.4 так, чтобы алгоритм заканчивал работу только после окрашивания всех вершин, то будут построены кратчайшие пути из выделенной вершины s в каждую из остальных вершин. Окрашенные дуги при этом образуют корневое ориентированное остовное дерево с корнем s.
Пример 11. Построить на данном взвешенном орграфе кратчайший путь
и
з
s=v1
в
f=v4.
l(s)=0
l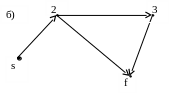
(2)=∞
l(3)=∞
l(f)=∞
p=s
l(s)=0
l(2)=min{∞;0+2}, θ(2)=s
l(3)=min{∞;0+∞}=∞
l(f)=min{∞;0+∞}=∞
p=2
l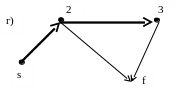
(s)=0
l(2)=2, θ(2)=s
l(3)=min{∞;2+1}=3, θ(3)=2
l(f)=min{∞;2+2}=4, θ(f)=2
p=3
l
(s)=0
l(2)=2, θ(2)=s
l(3)=3, θ(3)=2
l(f)=min{4;3+5}=4, θ(f)=2
p=f
Просматривая метки θ(f)=2, θ(2)=s, восстанавливаем кратчайший путь sv2f длиной l(f)=4. ■
Алгоритм Дейкстры может приводить к неправильному результату, если некоторые из дуг имеют отрицательный вес. Это подтверждает следующий пример.
П
ример
12.
Построить на данном взвешенном орграфе
кратчайший путь из s=v1
в f=v3.
l
(s)=0
l(2)=∞
l(f)=∞
p=s
l(s)=0
l(2)=min{∞;0+3}=3, θ(2)=s
l(f)=min{∞;0+2}=2, θ(f)=s
p=f
Алгоритм Дейкстры в качестве кратчайшего построил путь, состоящий из одной дуги с весом 2. В то же время, очевидно, существует более короткий путь sv2f с весом l=w(s,v2)+w(v2,f)=3+(-2)=1. ■
Решение задачи построения кратчайшего пути между двумя выделенными вершинами при наличии дуг отрицательного веса осуществимо с помощью алгоритма Форда (Ford L.R.). Этот алгоритм можно рассматривать как модификацию алгоритма Дейкстры, при которой:
на шаге 2 анализ l(i) производится для всех вершин; l(i) может уменьшаться как для неокрашенной, так и для окрашенной вершины; если l(i) для окрашенной вершины уменьшается, то окраска снимается с этой вершины и дуги (θ(i),i);
алгоритм завершает работу после того, как окрашены все вершины и на шаге 2 ни одна метка l(i) не изменяется.
Решение примера 12 с помощью алгоритма Форда показано на рис.18.
l(s)=0
l(2)=∞
l(f)=∞
p=s
l
(s)=0
l(2)=min{∞;0+3}=3, θ(2)=s
l(f)=min{∞;0+2}=2, θ(f)=s
p=f
l
(s)=0
l(2)=min{3;2+∞}=3, θ(2)=s
l(f)=min{2;2+0}=2, θ(f)=s
p=2
l(s)=0
l
(2)=min{3;3+0}=3,
θ(2)=s
l(f)=min{2;3+(-2)}=1, θ(f)=2
p=f
l
(s)=0
l(2)=min{3;1+∞}=3, θ(2)=s
l(f)=min{1;1+0}=1, θ(f)=2
все вершины уже окрашены.
С помощью алгоритма Форда построен кратчайший путь sv2f с весом l(f)=1.
Алгоритм Форда не решает задачу поиска кратчайшего пути между двумя выделенными вершинами, если в графе есть контур отрицательного веса. Признаком наличия такого контура является то, что при выполнении алгоритма число окрашиваний какой-либо вершины достигает количества вершин графа.