3. Пример расчета параметров парной линейной регрессии

В таблице 1.3 приведены данные о доле в расходах, направленной на потребление продуктов питания и заработной плате по нескольким регионам Уральского Федерального округа. Так как заработная плата характеризует одну из статей доходов домохозяйств, причем основную, а доля расходов на потребление продуктов питания – основную статью расходов, эти два показателя должны быть связаны между собой.

Х – заработная плата;

У – доля расходов на потребление продуктов питания, так как доля расходов зависит от заработной платы.

Задание: 1) параметризация: подобрать уравнение связи;

2) идентификация: идентифицировать параметры уравнения, измерить тесноту связи между фактором и результатом;

3) верификация: оценить надежность модели, сделать выводы;

4) прогнозирование:

• оценить уровень потребления при заданной заработной плате 58,0 млн.руб.

• оценить уровень потребления при заданной заработной плате равной ( +5%).

Порядок решения:

1. Параметризация: выберем для подбора параметров уравнение парной линейной регрессии, как получившее наибольшее распространение, наиболее легко идентифицируемое и интерпретируемое. Общий вид уравнения парной линейной регрессии в соответствии с формулой (4) следующий:

у = а + bх + 

2. На этапе идентификации необходимо вместо буквенных обозначений параметров а и b найти числа, соответствующие данной парной регрессии.

Найдем параметры а и b по формулам (7) и (8). Все предварительные расчеты приведены в таблице 3.

Таблица 1.3 – исходные данные для расчетов

№ п/п	Х, млн. руб	Y, %	Y·Х	Y2	Х2	ŶХ	Y-ŶХ	(Y-Ŷ)2	10 = |8/7|	(Х- )2
1	2	3	4	5	6	7	8	9	10	11
1	68,8	45,1	3102,9	2034,0	4733,4	51,0	-5,9	34,4	0,115	119,1
2	61,2	59,0	3610,8	3481,0	3745,4	53,7	5,3	28,0	0,099	11,0
3	59,9	57,2	3426,3	3271,8	3588,0	54,2	3,0	9,2	0,056	4,1
4	56,7	61,8	3504,1	3819,2	3214,9	55,3	6,5	41,9	0,117	1,4
5	55,0	58,8	3234,0	3457,4	3025,0	55,9	2,9	8,2	0,051	8,3
6	54,3	47,2	2563,0	2227,8	2948,5	56,2	-9,0	80,9	0,160	12,9
7	49,3	55,2	2721,4	3047,0	2430,5	58,0	-2,8	7,8	0,048	73,7
Итого	405,2	384,3	22162,3	21338,4	23685,8			210,3	0,646	230,47
Ср. знач.	57,9	54,9	3166,0	3048,3	3383,7			30,05	0,092	32,924

Также для определения параметров уравнения можно воспользоваться встроенной функцией категории «Статистические» → «ЛИНЕЙН». Подробнее об использовании этой функции см. Приложение 3.

Таким образом, по формуле (3) мы получили следующее уравнение парной линейной регрессии:

Вывод: при увеличении доходов на 1 млн. руб. потребление снижается на 360,7 тыс. руб.

Оценим тесноту связи между фактором и результатом с помощью линейного коэффициент корреляции (14), (9), (17):

Вывод: связь обратная, слабая. При увеличении доходов потребление снижается с невысокой вероятностью.

3. На этапе верификации оценим качество модели. Для этого рассчитаем ошибку аппроксимации, коэффициент детерминации, F-критерий, t-статистику.

Рассчитаем ошибку аппроксимации по формуле (29) и столбцу 10 таблицы 3:

, или 9,2%.

Вывод: Ошибка аппроксимации на превышает 8-10%, модель довольно точно описывает данные.

Рассчитаем коэффициент детерминации по формуле (15), (16) и (17) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:

Вывод: уравнение объясняет всего 12,5% вариации результата

Рассчитаем F-критерий по формулам (19) и (21) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:

Определим F_табл по таблице Приложения 1. Степени свободы числителя и знаменателя определим по таблице 2 (стр10). Число наблюдений – 7, параметр при х один – это b. Таким образом, k₁ = 1, k₂ = 5.

F_табл = 6,61

Вывод: F_факт < F_табл следовательно гипотезу о статистической незначимости уравнения связи нужно принять. Уравнение связи статистически незначимо, то есть значения параметров могли быть получены случайным образом.

Рассчитаем t-статистику для каждого параметра по формулам (22)-(28) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:

Определим t_табл для 5 степеней свободы и вероятности 0,95 по таблице Приложения 3. При поиске табличного значения учтем, что t-критерий симметричен относительно оси х, поэтому сравниваем значения фактические и табличные по модулю.

t_табл = 2,4669

Вывод: меньше t_табл следовательно с вероятностью 95% параметры r и b признаются статистически незначимыми.

В свою очередь, больше t_табл следовательно с вероятностью 95% параметр а признается статистически значимым.

4. прогнозирование: оценим уровень потребления при заданной заработной плате 58,0 млн. руб. на доверительном интервале с заданной вероятностью по формулам (30) и (31).

Для нахождения подставим в уравнение связи заданное значение х:

млн. руб.

Вывод: при уровне заработной платы на уровне 58 млн. руб. потребление составит 54,86 млн. руб. Однако точечный прогноз явно не реален, вероятность того, что реальное значение у совпадет с прогнозным , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал.

Стандартную ошибку прогноза определим по формуле (32) или воспользуемся встроенной функцией категории «Статистические» → «ЛИНЕЙН»:

Тогда среднюю ошибку прогноза определим по формуле (30). Для этого самостоятельно зададим требуемый уровень надежности (90%, 95% или 99%) и по таблице Приложения 3 для 5 = 7 - 2 степеней свободы определим t_табл. Пусть уровень надежности равен 90%, тогда t_табл = 2,0150.

млн. руб.

Тогда границы доверительного интервала составят:

(54,86-13,07) млн. руб. < < (54,86+13,07) млн. руб.

или 41,79 млн. руб. < < 67,93 млн. руб.

Вывод: с вероятностью 90% при заработной плате на уровне 58 млн. руб. потребление составит [41,79; 67,93].

Далее оценим уровень потребления при заданной заработной плате равной ( +5%).

Для этого сначала рассчитаем уровень заработной платы, для которого нужно построить прогноз. Средняя заработная плата по данным таблицы 3 составляет 57,9 млн. руб. Найдем уровень заработной платы (X_i) для построения прогноза как:

57,9 х (1 + 0,05) = 60,8 млн. руб.

5. Далее проведем все действия аналогично предыдущему прогнозу. Сначала оценим уровень потребления при заданной заработной плате 60,8 млн. руб. на интервале с заданной вероятностью по формулам (30) и (31).

Для нахождения подставим в уравнение связи заданное значение X_i:

млн. руб.

Вывод: при уровне заработной платы на уровне X_i = ( +5%) млн. руб. потребление составит 53,86 млн. руб. Однако точечный прогноз явно не реален, вероятность того, что реальное значение у совпадет с прогнозным , очень маленькая, практически нулевая. Поэтому для повышения надежности прогноза определим доверительный интервал прогноза.

Стандартная ошибку прогноза зависит от уравнения связи, поэтому для всех прогнозов по данному уравнению она постоянна. Поэтому, если не менять уровень надежности, то и средняя ошибка не изменится. Поэтому можно сразу построить прогноз:

(53,86-13,07) млн. руб. < < (53,86+13,07) млн. руб.

или 40,79 млн. руб. < < 66,93 млн. руб.

Вывод: с вероятностью 90% при заработной плате на уровне ( +5%) млн. руб. потребление составит [40,79; 66,93].

С помощью мастера диаграмм нанесем на график исходные данные и линии, характеризующие взаимосвязь, см. пример на рисунке 2.

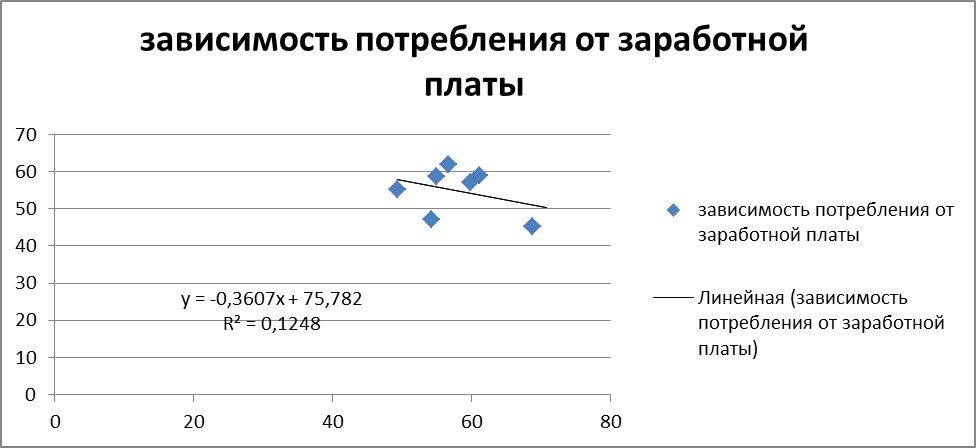
Рисунок 1.2 – Зависимость потребления от заработной платы

Для того, чтобы нанести на диаграмму уравнение связи и оценку аппроксимации (R²) воспользуемся функцией «Дополнительные параметры линии тренда» меню «Диаграмма», как на рисунке 3.

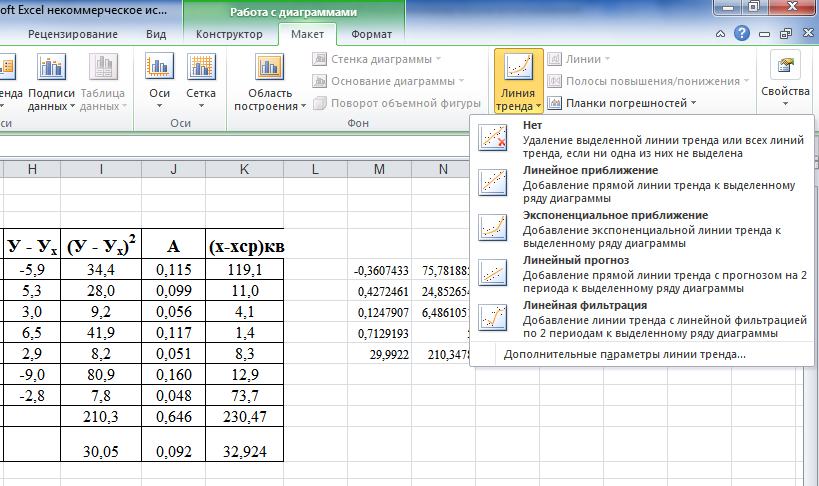
Рисунок 1.3 – Работа с диаграммой MS Excel