12

Трехфазные системы

Мы рассмотрели поверхностную энергию в системах, состоящих из двух объемных фаз с одной границей раздела (поверхностным слоем). Большой интерес и практическое значение представляют более сложные, а именно трехфазные системы, например, капля жидкости на твердой поверхности или пористое тело, частично заполненное жидкостью. В таких системах сосуществуют три объемные фазы, разделенные и в то же время связанные тремя поверхностными слоями, каждый из которых характеризуется собственным, независимым от других значением  (или ). Их соотношение определяет условия сосуществования объемных фаз, в частности условия механического равновесия. От этих величин зависит и поведение жидкости на поверхности твердого тела, — будет ли она растекаться или, наоборот, собираться в капли.

Возможность предвидения этих явлений и управления ими составляет научную основу крашения тканей, гидрофобизации твердых тел, флотации и многих других производственных процессов.

1.3 Смачивание

Рассмотрим сначала качественную картину явления. Если на поверхность твердого тела нанесена капля жидкости, то в такой системе присутствуют три различные поверхности раздела фаз: между твердым телом и газом (ТГ), жидкостью и газом (ЖГ) и твердым телом и жидкостью (ТЖ) с соответствующими натяжениями (_ТГ, _ЖГ, _ТЖ). Линию пересечения всех трех поверхностей раздела называют линией смачивания (замкнутая линия смачивания образует периметр смачивания). Исследуем два различных варианта поведения жидкой капли на твердой поверхности (рис. 4). Пусть в начальный момент капля имеет форму полусферы.

Условие самопроизвольного растекания капли определяется неравенством

_ТГ  >  _ТЖ

(при котором замена поверхности с большей свободной энергией на поверхность с меньшей свободной энергией в процессе растекания приведет к уменьшению запаса свободной энергии в системе).

Поскольку в этом процессе увеличивается свободная энергия поверхностного слоя на границе ЖГ, качественное рассмотрение позволяет предсказать возможность остановки процесса (рис. 5а) при значениях

_ТГ  -  _ТЖ    _ЖГ

или неограниченного растекания при

_ТГ  -  _ТЖ  >  _ЖГ

а в

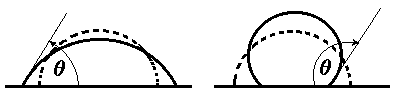
Рис. 5. Растекание капли на твердой поверхности. а – смачивание, в – несмачивание.

Штрихом показано положение капли в начальный момент

Во втором варианте, при

_ТГ  <  _ТЖ

очевидно, что уменьшение свободной поверхностной энергии системы S  приводит к самопроизвольному уменьшению площади контакта в процессе стягивания капли (рис.  5в).

В первом случае происходит смачивание, а во втором — несмачивание твердого тела жидкостью.

Мерой смачивания является краевой угол (), определяемый как угол между твердой поверхностью и касательной в точке соприкосновения трех фаз. Поскольку этому определению удовлетворяют два угла, условились отсчитывать  в сторону жидкой фазы.

В системах типа ТЖ₁Ж₂ и отсчитывают в сторону более полярной из двух жидких фаз (воды). Очевидно, что в случае смачивания и   <  90°, а при несмачивании    >  90°.

Таким образом, смачивание (рис. 5), измеряемое величиной  зависит от соотношения величин  на границах соприкасающихся фаз.

Рис. 6. Схема вывода формулы Юнга для краевого угла

Для получения количественной связи рассмотрим состояние равновесия для жидкости, смачивающей вертикальную твердую стенку (рис. 6) и химически с ней не взаимодействующую. При бесконечно малом смещении периметра смачивания l вниз на величину АВ  =  dh затрата работы на увеличение поверхности ТГ составляет (сила · расстояние или сила/длину · площадь) l dh ТГ (*) В то же время энергия системы уменьшается за счет уменьшения поверхностей ТЖ и ЖГ на величину:

l dh _ТЖ + l BC _ЖГ или l dh _ТЖ + l dh cos  _ЖГ (**)

В состоянии равновесия изменение свободной энергии dF  =  0 и, приравнивая эти выражения (* и **), получаем:

l dh _ТГ = l dh _ТЖ + l dh cos _ЖГ

Или после деления на l dh :

_ТГ = _ТЖ + cos _ЖГ

откуда

(1.18)

Уравнение (1.18), определяющее условия смачивания, — математическое выражение закона Юнга. Анализ его подтверждает следствия, полученные на основе качественных представлений:

_ТГ  >  _ТЖ cos  >  0   <  90 (смачивание)

_ТГ  <  _ТЖ cos  <  0   >  90 (несмачивание) (1.19)

_ТГ  =  _ТЖ cos  =  0   =  90

Поскольку величины _ТГ и _ТЖ ,  входящие в уравнение (1.8), обычно неизвестны, целесообразно рассмотреть молекулярные силы и их работу, определяющую значения всех  _ij , а следовательно и .

а б Рис. 7. Иллюстрация понятия когезии и адгезии.

Назовем силами когезии (слипания) те, которые действуют между молекулами внутри фазы, а адгезии (прилипания) между молекулами, находящимися в разных фазах. В соответствии с этим работа когезии Wc определяется как работа, необходимая для разрыва однородной объемной фазы. Относят ее к единице площади разрыва. Как видно из рис. 7а, эта работа разрыва (в плоскости А) равна Wc = 2 ЖГ (1.20) поскольку при этом образуются две новых поверхности ЖГ.

Работа адгезии W_a, также относимая к единице площади, определяется как работа разрыва межфазного поверхностного слоя (рис. 7б). Затрачивается она на образование двух новых поверхностей и выигрывается за счет исчезновения свободной энергии исходной межфазной границы. Для системы ТЖ эта работа (рис. 7б) равна:

W_a = _ЖГ + _ТГ - _ТЖ (1.21)

Это выражение называется уравнением Дюпре. Из него вытекает заключение, что межфазное натяжение _ТЖ тем меньше, чем больше межфазное взаимодействие на этой границе раздела. Физический смысл этого утверждения заключается в том, что свободная энергия уменьшается за счет работы сил взаимодействия.

Из уравнений (1.18) и (1.20) получаем для работы адгезии следующее выражение:

W_a = _ЖГ (1 + cos ) (1.22)

Используя уравнение (1.22), можно вычислить W_a по экспериментально измеренным значениям _ЖГ и cos . Оно показывает, что чем больше адгезия, тем больше cos , т.е. смачивание. Таким образом, силы межфазного взаимодействия (адгезионные силы) стремятся растянуть каплю, в то время как силы когезии стягивают каплю до полусферы, препятствуя растеканию, поскольку с ростом знаменателя уравнения (1.18), пропорционального W_c, уменьшается абсолютная величина cos . Уравнение (1.22) позволяет выразить условие смачивания (cos ) в терминах работы. С учетом уравнения (1.20) находим:

W_a  >  0,5 W_c (1.23)

Для случая полного несмачивания ( = 180°, cos   = -1) уравнение (1.22) дает: W_a = 0. Этот результат не имеет физического смысла, поскольку нельзя представить себе полное отсутствие взаимодействия между двумя соприкасающимися фазами. Действительно, не известны случаи, когда измеренные краевые углы > 150°.

При W_a = W_c и тем более при W_a > W_c растекание становится неограниченным, поскольку  = 0, согласно (1.22), и _ТГ  >  _ТЖ  +  _ЖГ. Разность W_a – W_c называют коэффициентом растекания.

Уравнения (1.20 - 1.22) позволяют оценить искомую величину и на основании значений параметров W_a и W_c, которые можно всегда связать (хотя бы качественно) с природой фаз, с их полярностью. Так, вода хорошо смачивает стекло, алюмосиликаты, ионные кристаллы и другие поверхности, несущие ионы или образующие их в процессе гидратации. В этих случаях ион-дипольное взаимодействие (W_a) больше диполь-дипольного (W_c). В то же время вода не смачивает парафин и другие неполярные вещества, т.к.у W_c для воды, сильно полярной жидкости, весьма значительна. Гептан, этиловый спирт, бензол и другие жидкости с низкими значениями _ЖГ и W_c смачивают практически любую твердую поверхность. Наоборот, ртуть (_ЖГ  485 эрг/см²), как правило, не смачивает твердые поверхности, за исключением некоторых металлов.

Р ис. 8. Формирование краевых углов натекания и оттекания

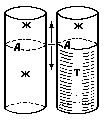
Закономерности смачивания выполняются для всех поверхностях жидкостей только на идеально гладких и однородных поверхностях твердых тел. На поверхности реальных тел обязательно имеются шероховатости (поры, трещины, впадины, выпуклости, загрязнения), которые сказываются на величине измеряемого краевого угла. Также на величину  влияет и размер капли. При увеличении капли формируется предельный угол - краевой угол натекания (н), а при ее уменьшении - предельный угол - краевой угол оттекания (от). Наглядная демонстрация этого процесса при наклоне

пластинки представлена на рис. 8. Эти отклонения от равновесных (истинных) значений

_н  >  _от

_ист. называются гестерезисом краевого угла. Сравнивая измеренные величины  при различных условиях можно оценить загрязнение и шероховатость поверхности:

cos _R  =  R cos _ист. (1.24)

где _R - реальный краевой угол для данной поверхности,

_ист. – краевой угол идеальной поверхности,

R – мера шероховатости (загрязненности).

Для приближенной оценки иногда считают, что равновесный (истинный) угол смачивания равен полусумме предельных углов натекания и оттекания.