Пример решения задачи 2

Выполним расчёт бруса, схема которого приведена на рис. 2.1, а при следующих значениях:

1-й вариант: l = 0,2 м; q = - 80 кН/м; P =12 кН; А = 2 см²;

2-й вариант: l = 0,2 м; q = 80 кН/м; P = - 12 кН; А = 2 см².

Сначала выполним чертёж бруса по заданным значениям: вид бруса показан на рис. 2.2, а, б.

1. Построение эпюры продольных сил

Определение продольной силы для бруса с заделкой удобно выполнять, как показано выше, рассматривая отсечённую часть со стороны свободного края, так как при этом не обязательно определение опорных реакций. Согласно методу сечений получена формула продольной силы (2.2).

Выполним вычисления по (2.2) для указанных двух вариантов значений.

1-й вариант

Подставляем q = - 80 кН/м и P =12кН в выражение продольной силы (2.2) и получаем линейную функцию

.

Вычислим значения силы в начале бруса (при z = 0) и в конце (при z = l). Получим граничные значения продольной силы:

при z = 0 кН;

при z = l = 0,2 м кН.

Построим эпюру (рис.2.2, а).

Сначала непосредственно под чертежом самого бруса проводим линию, параллельную оси бруса, она называется базисной линией. Далее в характерных сечениях (соответствующих началу и концу бруса) откладываем значения силы : положительное12 кН - вверх от линии, отрицательное (- 4 кН) – вниз. Полученные точки соединяем наклонной прямой. График штрихуют перпендикулярно к базисной линии и ставят знак силы (+ или –).

2-й вариант

Подставляем q = 80 кН/м и P = -12кН в выражение продольной силы (2.2) и получаем

.

Вычислим граничные значения продольной силы:

при z = 0 кН;

при z = l = 0,2 м кН.

Построим эпюру (рис. 2.2, б): сначала также под чертежом самого бруса проводим базисную линию; далее в сечениях, соответствующих началу и концу бруса, откладываем значения силы (отрицательное (-12 кН) ‒ вниз от линии, положительное 4 кН – вверх); полученные точки соединяем наклонной прямой; штрихуем перпендикулярно к базисной линии и ставим знак силы (+ или – ).

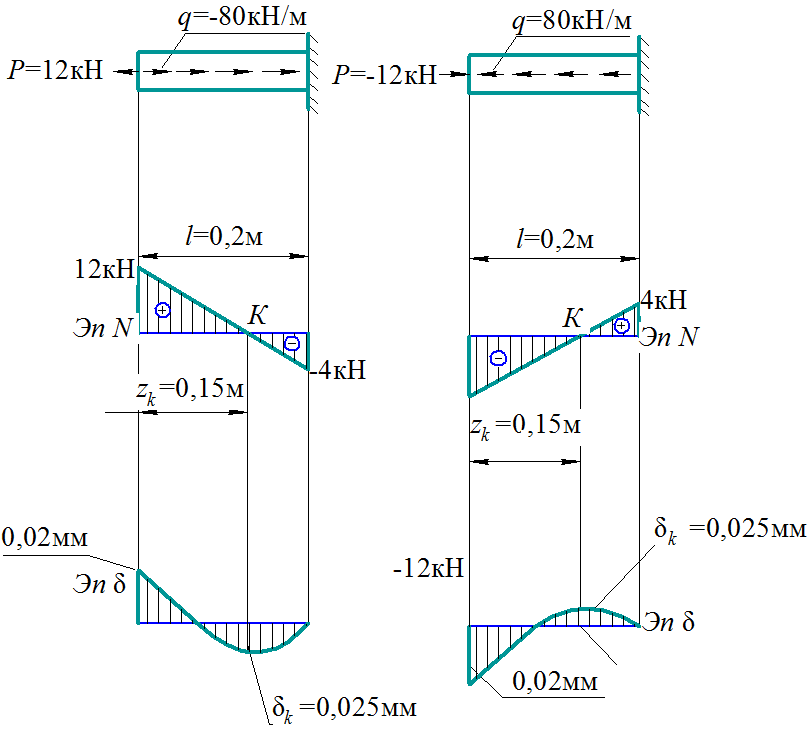
Для 1-го варианта значений Для 2-го варианта значений

а б

Рис. 2.2

2. Вычисление нормальных напряжений и проверка прочности

Продольная сила является результирующей нормальных напряжений , которые распределены равномерно по поперечному сечению бруса, т. е. по (1.1) .

Знак напряжения зависит от знака силы , а величина напряжения изменяется при изменении силы.

1-й вариант

Требуемую проверку прочности (проверочный расчёт) выполним, составив условие прочности по (2.3).

Сначала определим функцию :

,

Найдём значения в начале и в конце бруса:

при ,

при .

Наибольшее напряжение по абсолютной величине оказалось равным

.

Подставив значения в (2.3), получаем

.

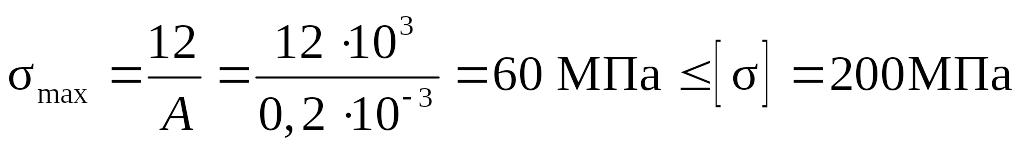Отсюда делаем заключение: условие прочности выполняется.

Расчёт для 2-го варианта значений аналогичен.

3. Построение эпюры продольных перемещений и проверка жёсткости

Для построения эпюры перемещений вычислим, используя формулы (2.5), перемещения некоторых характерных сечений. По этим значениям под брусом изобразим эпюру перемещений (график изменения перемещений вдоль бруса).

Далее по эпюре перемещений нужно установить значение наибольшего перемещения δ_max и выполнить проверку жёсткости по условию (2.6).

1-й вариант

Вычислим абсолютную деформацию бруса Δl по (2.5).

Можно подставить значения P, q и ЕА в окончательное выражение (2.5). Но можно подстановку значений сделать в продольную силу N (2.2) и далее интегрировать по (2.4). Результат будет одинаков.

Например, выполним интегрирование, используя (2.4).

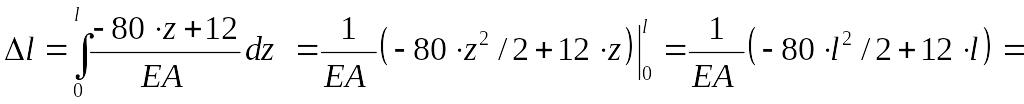
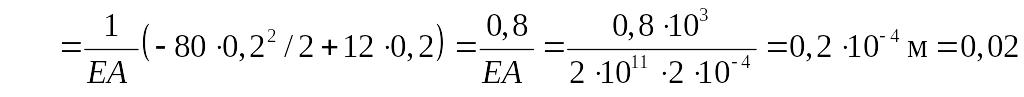мм.

Далее определим перемещения двух характерных сечений: в начале и в конце бруса.

Для бруса с жёсткой заделкой удобно идти в расчётах от заделки, в которой перемещение равно 0:

.

Перемещение на свободном краю бруса запишем согласно (2.7):

мм.

Заметим, что эпюра N имеет линейный характер (рис. 2.2), но для наших значений в сечении К получено пересечение прямой N с базисной линией, т.е. для этого сечения продольная сила N_к=0. Тогда согласно выражению интеграла (2.5), в сечении К подынтегральная функция (это производная интеграла) равна 0, и поэтому здесь будет экстремум значения интеграла. Значит, в сечении К должен быть экстремум перемещения, и в этом сечении получим перегиб параболы перемещений.

В виду этого вычислим значение перемещения сечения К (перемещения δ_к) и уточним график перемещений.

Обозначим координату сечения К как z_к и вычислим значение экстремального перемещения δ_к. Так как продольная сила в сечении К

N_к = q∙z_к + P = 0,

то координата z_к 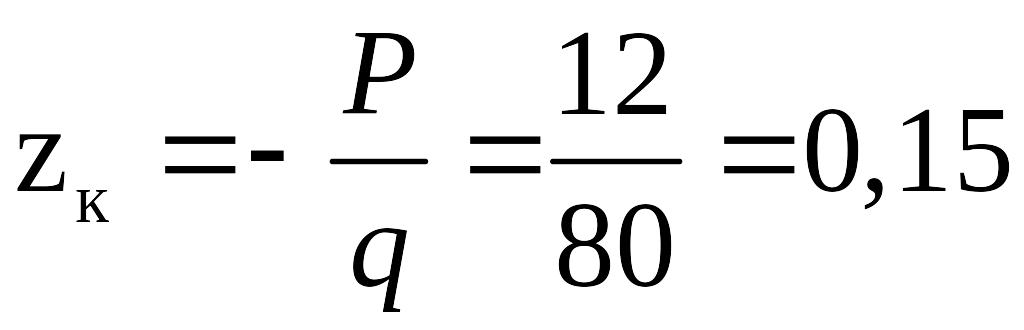м.

Перемещение δ_к фактически равно деформации куска бруса от заделки до сечения К.

Удобно сначала вычислить деформацию ∆l(z_к) куска бруса длиной z_к=0,15 м, отсчитывая расстояние z от свободного края.

Значение ∆l(z_к) по (2.5) равно

Δl(z_к) = =

_.

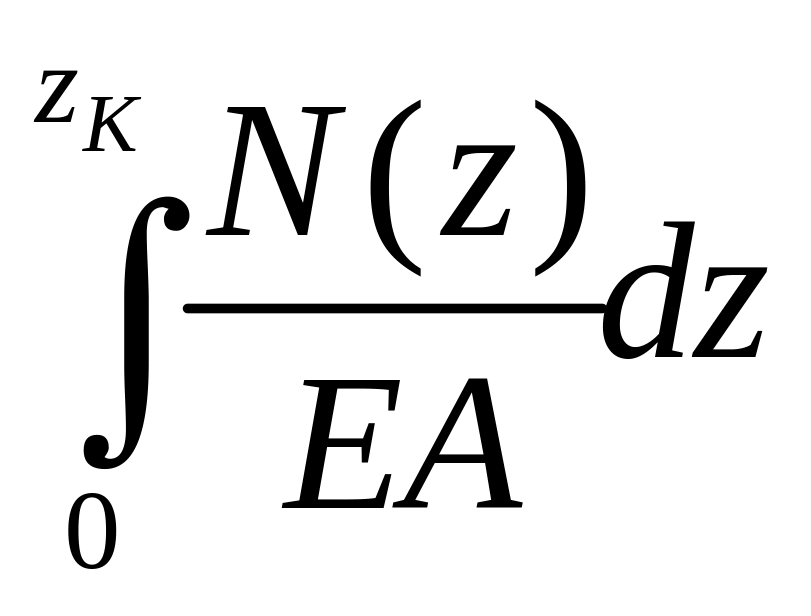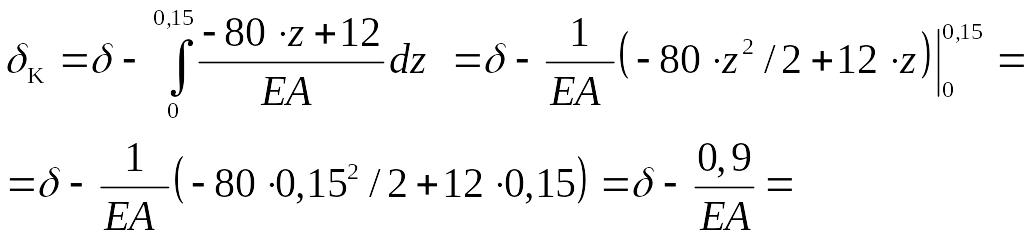
Теперь через ∆l(z_к) запишем перемещение свободного края бруса δ, используя (2.7).

δ= δ_к + Δl(z_к).

Отсюда получаем искомое перемещение δ_к сечения К в виде

δ_к = δ - Δl(z_к) = δ - = δ -

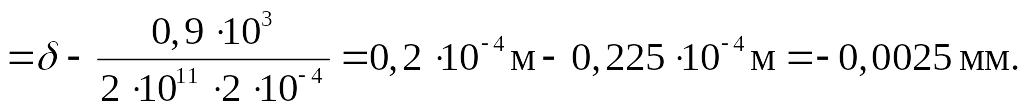
Проведём базисную линию (рис. 2.2), и перпендикулярно отложим в выбранном масштабе полученные значения перемещений: на краю бруса вверх δ = 0,02мм; в сечении К вниз δ_К = -0,0025мм. Далее проводим параболу с перегибом для сечения К.

Проверим условие жёсткости.

Для этого из эпюры перемещений возьмём наибольшее перемещение мм и запишем условие жёсткости заданного бруса, используя общий вид условия жёсткости (2.6)

=1 мм,

значит, условие жёсткости выполняется.

Расчёт для 2-го варианта значений аналогичен.

Таблица 2.1. Исходные значения к задаче 2

Номер Варианта	Сила P, кН	Интенсивность распределённой нагрузки q, кН/м	Площадь сечения А, см2	Длина бруса l, м
1	20	-80	4	0,3
2	-20	180	3	0,3
3	25	60	3	0,5
4	-25	170	5	0,5
5	30	-50	10	0,5
6	-30	150	8	0,2
7	40	-50	5	0,4
8	-40	170	7	0,3
9	45	-100	2	0,4
10	-45	-100	6	0,4
11	50	-70	4	0,4
12	-50	60	5	0,15
13	35	-160	5	0,15
14	-35	160	3	0,3
15	55	60	2	0,4
16	-55	90	6	0,4
17	37	-60	3	0,2
18	-37	160	7	0,6
19	42	90	7	0,6
20	-42	130	5	0,3
21	23	-120	10	0,3
22	-23	-100	12	0,2
23	32	170	5	0,25
24	-32	140	5	0,25
25	48	-150	6	0,5
26	-48	-80	4	0,3
27	-33	180	3	0,3
28	33	-110	3	0,5
29	-27	120	5	0,5
30	27	-50	10	0,5