Задача 9 Определение допускаемой высоты падения груза на балку Условие задачи

На стальную двутавровую балку, свободно лежащую на двух опорах, схемы которой приведены в табл. 9.1, падает груз весом Р. Номер двутавра, значение длины балки l и веса Р даны в табл. 9.2.

Требуется:

Определить допускаемую высоту падения груза для 2-х случаев опирания балки:

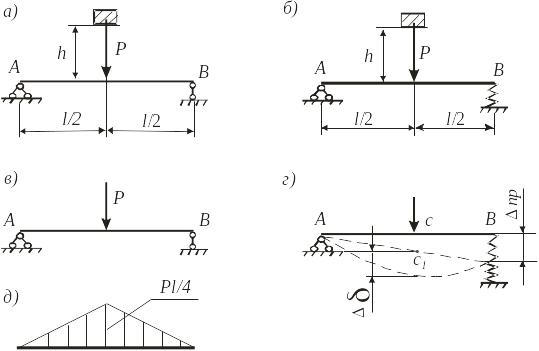
1) опоры абсолютно жёсткие (рис. 9.2, а);

2) одна их опор является упругоподатливой (рис. 9.2, б), её податливостью λ задана в табл. 9.2 (податливость – это осадка опоры от груза весом 1 Н).

Теоретические основы решения

При падении груза балка или рама (рис. 9.1) испытывает ударное воздействие (ударную нагрузку). Такое воздействие возникает и в других случаях, например, при забивке свай, при ковке.

Отличительная особенность такого нагружения ‒ это очень короткий период воздействия (время удара находится в пределах от 10^-3 до 10^-8 с).

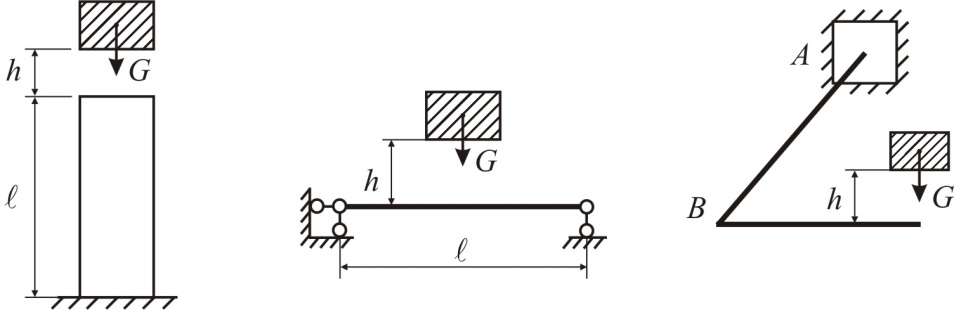
Рис. 9.1

При расчёте на удар обычно используют методику, основанную на законе сохранения энергии, согласно которой ударный характер нагрузки учитывается введением динамического коэффициента к_д. Согласно этой методике условие прочности при ударной нагрузке имеет вид

, (9.1)

где  наибольшее динамическое напряжение;  наибольшее статическое напряжение, которое при падении груза определяется как наибольшее напряжение от статического приложения силы, равной весу груза P;  допускаемое напряжение для материала ударяемой конструкции; к_д  динамический коэффициент.

Если расчёт проводится без учёта собственной массы ударяемого тела, динамический коэффициент к_д определяется через высоту падения h и статическое перемещение как

.

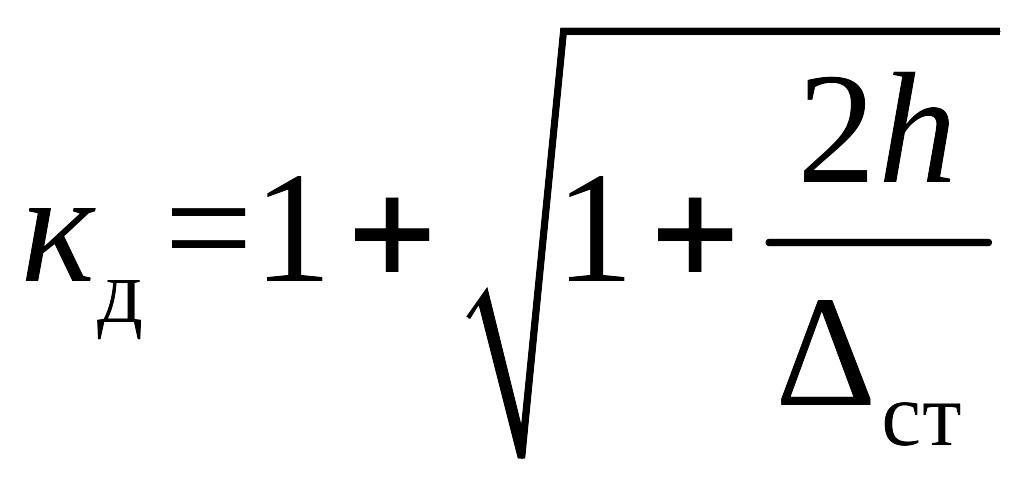В тех случаях, когда высота падения значительно больше величины ,

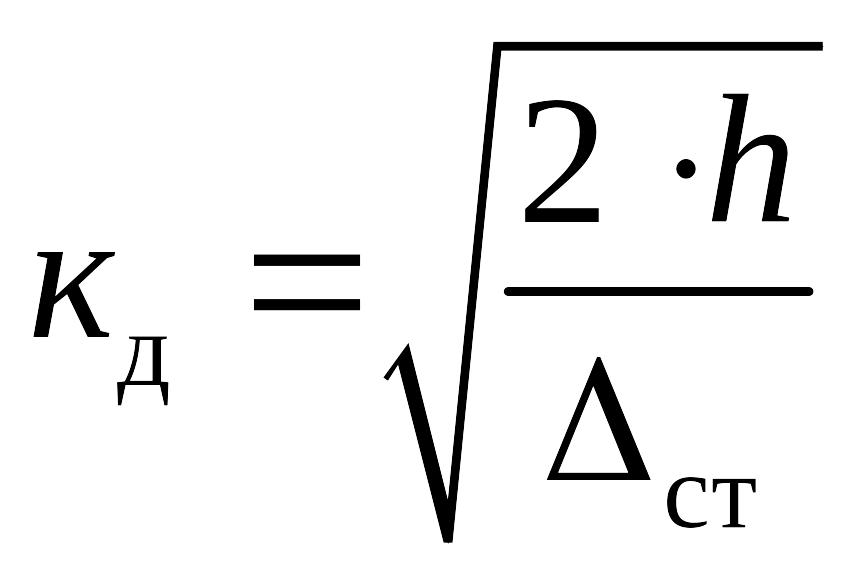. (9.2)

Как следует из условия прочности (9.1), динамический коэффициент показывает, во сколько раз увеличились напряжения (значит, и деформации) при изменении статического приложения нагрузки на ударное.

Пример решения задачи 9

Выполним расчёт для балки, показанной на рис. 9.2. На стальную балку с неизвестной высоты h падает груз Р = 500 Н. Значение длины = 4 м, сечение балки - двутавр № 24.

Определим допустимую высоту падения груза при абсолютно жёстких опорах и для случая, когда правую опору В заменили на упруго-податливую с податливостью λ = 2,5·10^-5 м/Н.

1. Условие прочности балки при ударе

Чтобы выполнить расчёт на удар по условию (9.1), необходимо знать напряжение и динамический коэффициент к_д, определяемый по (9.2) через перемещение в месте удара от статического действия нагрузки Р.

На рис. 9.2, в показано статическое приложение силы Р, при котором наибольшее статическое напряжение

,

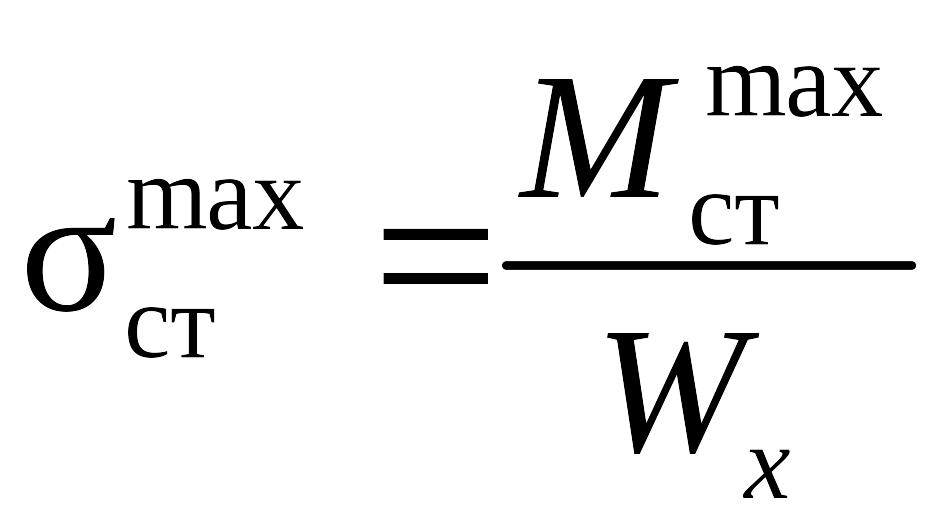где – наибольшее значение изгибающего момента от статической силы Р; − осевой момент сопротивления сечения балки.

Заданная балка на жёстких опорах	Заданная балка с упругоподатливой опорой В
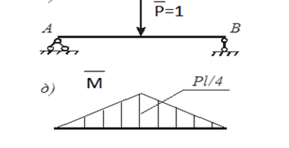
Грузовое состояние и эпюра грузовых моментов	г) Единичное состояние и эпюра единичных моментов
	д) - Вид деформирования балки с упруго-податливой опорой

Рис. 9.2

После подстановки напряжения и динамического коэффициента (9.2) в (9.1) имеем условие прочности балки в виде:

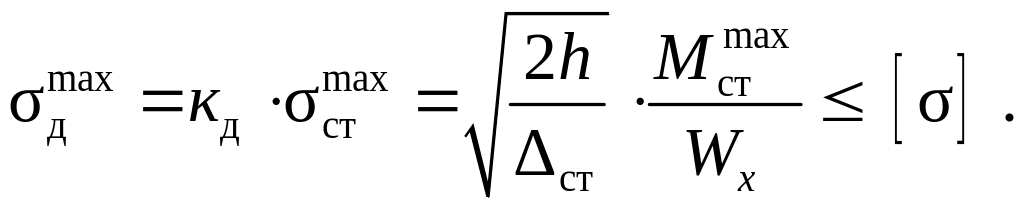(9.3)

Здесь – перемещение в месте удара (в нашем случае это прогиб балки Δ в сечении С); h – неизвестная высота падения груза.