8. Уравнения высших порядков, допускающие понижение порядка
Уравнениями высших порядков
называются уравнения содержащие
производные второго, третьего и т.д.
порядков. В общем случае такие уравнения
решаются намного сложнее, чем уравнения
первого порядка и выделим некоторые
частные случаи, когда либо уравнения
высших порядков интегрируются в конечном
виде, либо порядок этого уравнения можно
понизить и свести к уже рассмотренным
случаям интегрирования дифференциальных
уравнений. При интегировании
дифференциальных уравнений высших
порядков следует помнить, что решение
дифференциального уравнения
-го
порядка должно содержать
произвольных постоянных.
1.
,
т.е. правая часть зависит только от
аргумента
.
Функция
предполагается непрерывной на сегменте
.
,
,
,
………..
.
В результате мы получили общее решение данного уравнения, и общее решение содержит кратных интегралов. Если известно одно частное решение , то при решении данного уравнения можно обойтись без -кратного интегрирования. Произведем замену:
,
…. ,
,
,
,
,
,
…,
,
– общее решение данного уравнения.
Пример:
.
.
.
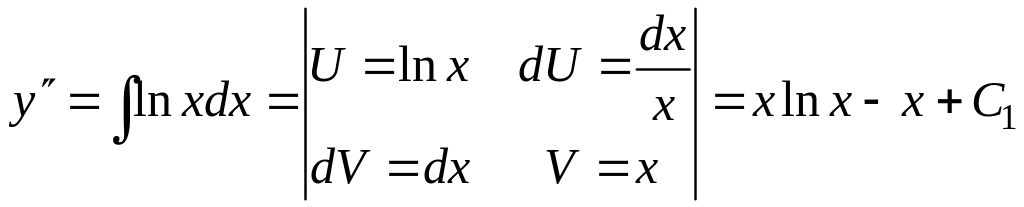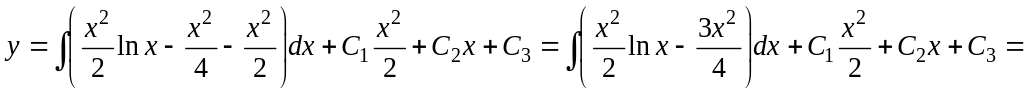
2.
,
т.е. уравнение
-го
порядка не содержащее аргумента
.
Произведем замену
,
тогда
,
получаем
.
Допустим, что это уравнение разрешимо
относительно производной
,
тогда мы получаем уравнение с разделяющимися
переменными:
.
Отсюда находим общее решение
,
тогда
,
мы получили уравнение вида рассмотренного
в пункте 1.
,
т.е. решение находится через квадратур.
Пример:
.
Сделаем замену
,
,
подставим в уравнение, получаем
.
,
.
(1)
Попробуем выразить :
,
,
(2)
Сложим (1) и (2) , получим
,
производя обратную замену, имеем:
,
,
.
3.
,
т.е. уравнение не содержит аргумента
и искомой функции
.
Обозначим
,
тогда
,
получаем
.
Допустим, что это уравнение разрешимо
относительно
,
т.е.
.
Умножим обе части уравнения на
,
получим
,
интегрируя, имеем:
,
.
Получили уравнение с разделяющимися
переменными, разрешая его, получаем:
.
Возвращаясь к переменной
:
.
В результате получили уравнение вида
(1), которое интегрируется с помощью
квадратур и в результате интегрирования
мы получили еще
произвольные постоянные.
Пример:
.
Сделаем замену
,
,
подставим в уравнение, получаем
.
Умножив на
обе части уравнения, получим
,
отсюда
,
интегрируем:
,
,
,
,
,
,
Аналогично примеру из пункта 2, выразим
,
сложив с предыдущим, получим:
.
Сделав обратную замену:
,
,
.
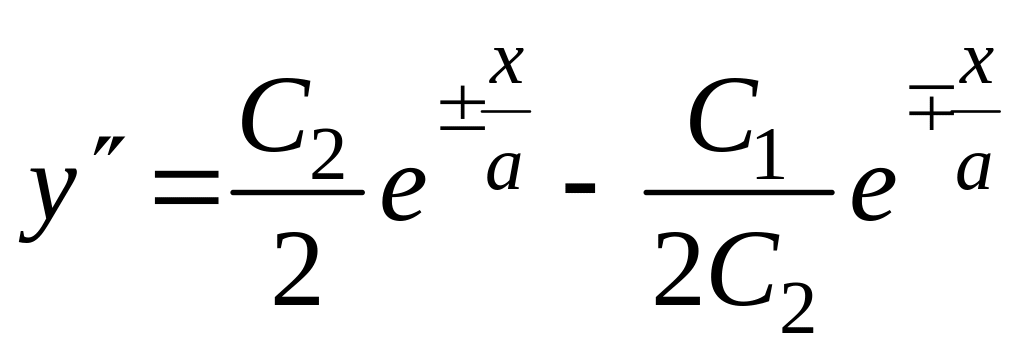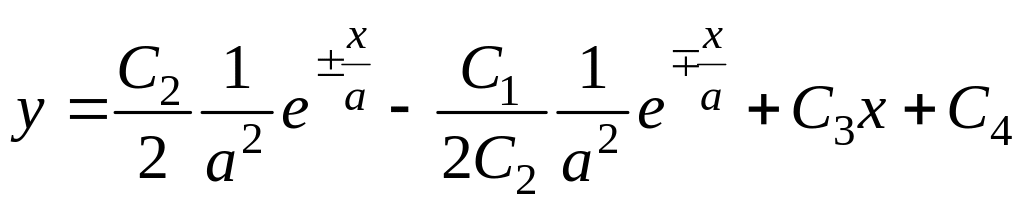4.
,
т.е. уравнение не содержит искомую
функцию
и её первые производные.
Порядок этого уравнения можно понизить
на
единиц с помощью замены
,
тогда
,
…,
,
получаем
.
Если это уравнение удается разрешить,
то соответственно находится и
.
Пример:
.
Сделаем замену
,
,
подставим в уравнение, получаем
.
,
,
,
,
,
.
5.
,
т.е. уравнение не содержит переменной
.
Порядок этого уравнения можно понизить
на единицу, если обозначить
,
и считать
аргументом
,
т.е.
,
тогда
,
.
В результате мы получаем, что данное уравнение будет зависеть от , и её производных.
Пример:
.
Сделаем замену
,
,
подставим в уравнение, получаем
,
получили уравнение Бернулли, т.е.
уравнение, сводящиеся к ЛНУ. Обозначим
,
и уравнение примет вид:
.
– это ЛНУ.
Решим в начале ЛОУ:
.
,
тогда
,
подставляем в уравнение:
,
.
Возвращаясь обратно к переменной
,
получаем
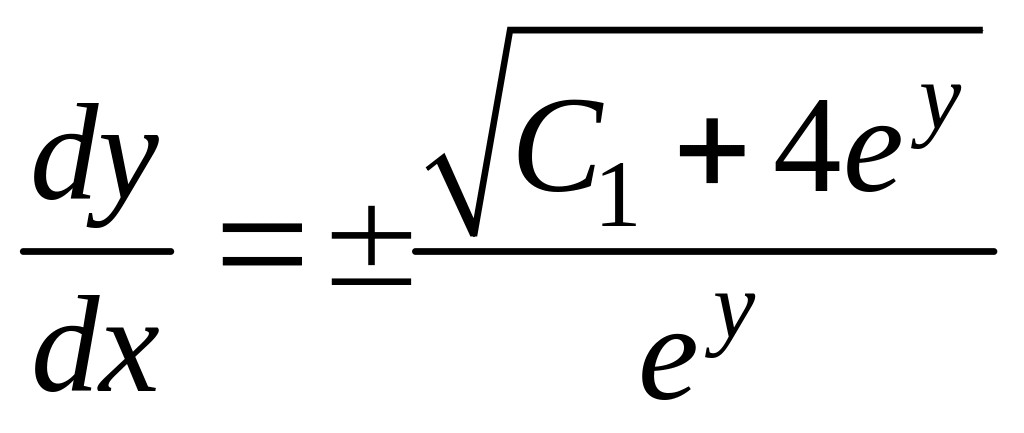
– общий интеграл данного уравнения.