6. Уравнения в полных дифференциалах
Пусть задано уравнение первого порядка в виде
.
(1)
Если левая часть уравнения (1) есть полный дифференциал некоторой функции, то уравнение (1) называется уравнением в полных дифференциалах.
Обозначим функцию
,
для которой
,
тогда
,
– общий интеграл уравнения (1).
Следовательно, мы должны выяснить, при каких условиях уравнение (1) будет в полных дифференциалах и как найти функцию .
Из теории функции нескольких переменных
мы знаем, что для того, чтобы выражение
было полным дифференциалом некоторой
функции необходимо и достаточно, что
бы
в области
.
Таким образом, получим, что для того,
что бы уравнение (1) было уравнением в
полных дифференциалах необходимо и
достаточно, что бы
.
Для нахождения функции по её полному дифференциалу можно пользоваться неопределенным интегралом.
Имеем:
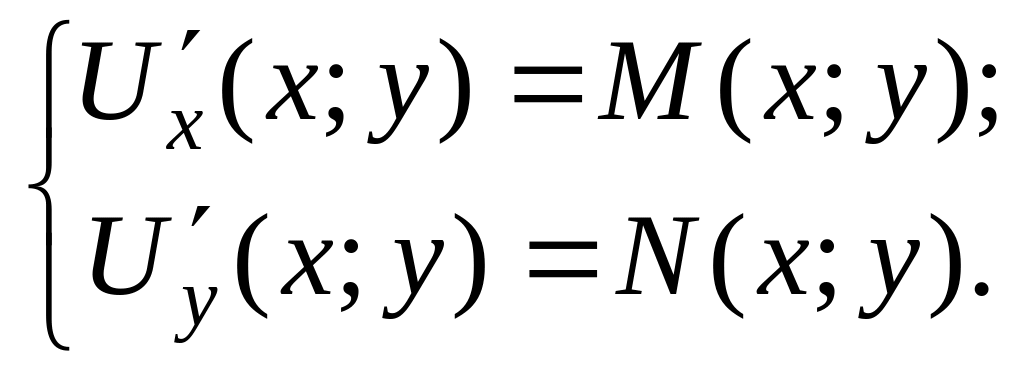
Отсюда,
.
Подставляя во второе уравнение системы,
находим
и, следовательно, получаем
.
Затем записываем ответ в виде общего
интеграла
.
Пример: 1)
.
,
,
,
,
,
,
,
–
общий интеграл.
2)
– это уравнение является однородным
уравнением. Проверим, не будет ли оно
уравнением в полных дифференциалах:
,
уравнение в полных дифференциалах.
,
,
,
,
.
3)
.
,
уравнение в полных дифференциалах.
,
,
,
,
,
.
7. Интегрирующий множитель
Пусть задано уравнение первого порядка в виде
(1)
и оно не является уравнением в полных
дифференциалах, т.е.
в некоторой области
.
В некоторых случаях существует такая
функция
,
что после умножения уравнения (1) на эту
функцию получаем уравнение в полных
дифференциалах, т.е. уравнение
.
(2)
уже является уравнением в полных дифференциалах.
Так как
,
то уравнения (1) и (2) имеют одно и то же
множество решений.
Множитель
в этом случае называется интегрирующим
множителем.
Задача состоит в том, чтобы найти, если
это возможно, интегрирующий множитель.
Так как уравнение (2) должно быть уравнением
в полных дифференциалах, то справедливо
равенство:
.
,
.
(3)
Получаем уравнения в частных производных первого порядка. Такие уравнения решаются довольно сложно, поэтому рассмотрим частные случаи, когда уравнение (3) разрешимо.
Пусть
,
тогда
,
.
,
.
Если
есть функция
,
то последнее уравнение является
уравнением с разделяющимися переменными
и, интегрируя его, получаем:
,
.
Так как нам нужен хотя бы один множитель, тогда положим , отсюда
.
Пусть
,
тогда
,
.
,
.
Если
,
то аналогично предыдущему, получаем
.
Пример: 1)
.
Найдем
,
.
Вычислим
:
.
Умножим уравнение на
,
получим:
Находим снова
,
,
а значит получили уравнение в полных
дифференциалах, решаем его:
.
.
.
2)
.
Найдем
,
.
Вычислим
:
.
.
Находим снова
,
,
т.е. уравнение в полных дифференциалах
,
.
.