ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Литература

1. Степанов В.В. Курс дифференциальных уравнений. 1950

2. Матвеев Н.М. Дифференциальные уравнения, 1999

3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М. 1982

4. Пискунов Н.С. Дифференциальное и интегральное исчисление, т II, 2002

5. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. 2001

1. ОСНОВНЫЕ ПОНЯТИЯ

Пусть независимая переменная, а – функция, зависящая от переменной .

Дифференциальными уравнениями (Д.У.) называются уравнения, содержащие независимую переменную, искомую функцию, и её производные.

Общий вид такого уравнения .

Уравнение может не содержать независимой переменной или искомой функции, но обязательно содержит производную.

Порядком ДУ называют наивысший порядок производной, входящей в уравнение. Например, – уравнение второго порядка,

– уравнение первого порядка.

Если мы имеем искомую функцию, как функцию одной переменной, т.е. , то уравнение называется обыкновенным ДУ.

Если же искомая функция зависит от нескольких переменных, т.е. , то ДУ содержит частные производные и называется уравнением в частных производных.

В дальнейшем мы будем рссматривать только обыкновенные ДУ.

Рассмотрим уравнение первого порядка, его общий вид

или (1)

Уравнение (1) называется уравнением первого порядка, разрешенным относительно производной. В правой части уравнения (1) находится функция двух переменных и область определения этой функции будет областью определения уравнения (1).

Функция называется решением уравнения (1) на промежутке , если она удовлетворяет этому уравнению на всем промежутке , т.е. .

П ромежуток , на котором существует решение, называется областью существования решения, и он должен содержаться внутри области определения уравнения. Отсюда видно так же, что для того, чтобы функция была решением на промежутке , необходимо, что бы она была дифференцируемой, т.е. имела конечную производную.

Кривые на плоскости XY соответсвующие решениям уравнения называются интегральными кривыми, а процесс решения дифференциального уравнения называется интегрированием ДУ. Другими словами, интегральные кривые это графики решения уравнения.

Примеры: 1) ,

(рис.1)

2) ,

Последний интеграл не берется в конечном виде, т.е. не вычисляется через элементарные функции, хотя он существует. В этом случае считается также, что решение уравнения найдено, но оно выражено через квадратуры.

Уравнение считается решенным, если его решение получено либо в явном виде, либо в квадратурах.

Из рассмотренных примеров видно, что ДУ имеет не одно решение, а бесконечно много решений, зависящих от постоянной С.

Кроме задачи решения ДУ в теории ДУ рассматривается задача нахождения одного решения, удовлетворяющего определенным условиям. В частности наиболее часто рассматривается задача Коши: найти решение уравнения (1), удовлетворяющее условию , где – заданные начальные условия. С геометрической точки зрения задача Коши состоит в нахождении интегральной кривой, проходящей через фиксированную точку .

Примеры: Из всех решений уравнения найти то, которое удовлетворяет условию .

Из рассмотренных примеров видно, что решение ДУ содержит произвольную постоянную, т.е. . Такое решение называется общим решением уравнения (1), решение, удовлетворяющее задаче Коши и начальным условиям называется частным решением. Например, – это общее решение, а – частное решение, удовлетворяющее условию . Кроме этого, если решение найдено в виде , то говорят, что оно найдено в явном виде. Если же решение получено в другом виде, например, для уравнения решение , то решение найдено в неявном виде, говорят, что получен общий интеграл уравнения.

2. Задачи, приводящие к дифференциальным уравнениям. Поле направлений уравнений первого порядка

Задача 1. Материальная точка с массой движется прямолинейно под действием силы . Известно, что пропорционально времени , которое прошло с момента начала движения. Сила сопротивления среды пропорциональная скорости движения . Найти зависимость скорости движения точки от времени, т.е. , причем в начальный момент.

Решение: Воспользуемся вторым законом Ньютона ,

где – ускорение ,

Это уравнение является линейным неоднородным уравнением. Можно проверить, что его решением с учетом начального условия будет

.

Задача 2. Найти кривые, у которых отрезок касательной, заключенный между осями координат, делится попалам в точке касания. (рис.2)

Точка М имеет координаты . Пользуясь геометрическим смыслом производной, получаем

,

,

,

– гиперболы.

К ДУ приводят и многие другие задачи, особенно в физике.

Рассмотрим вновь уравнение первого порядка , с областью определения . Точка , тогда получаем , т.е. в точке производная от искомой функции есть фиксированное конечное число. Пользуясь геометрическим смыслом производной, получаем что . Это значит, что в точке определен угол или определенно направление касательной к интегральной кривой. Рассматривая другие точки области , мы получаем, что в каждой из них определенно направление касательной к интегральной кривой.

Совокупность всех направлений в каждой точке создает поле направлений.

Интегральная кривая должна быть проведена так, чтобы в каждой своей точке направление касательной совпадало с направлением поля. Для построения интегральных кривых через поле направлений используется метод изоклин.

Изоклиной называется линия, вдоль которой направление поля одно и тоже.

Например, изоклина нуля – это линия, для каждой точки которой поле направления параллельно оси ОХ. , .

И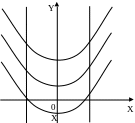 зоклины находятся из условия , тогда . Обычно рассматриваются значения , , ( )

Примеры:

Пусть

При , т.е. – функция возрастает; при , т.е. – убывает.

В некоторых случаях рассматривается и обратная задача восстановления уравнения по решению этого уравнения.

Пример: составить ДУ общим решением которого является функция .

Найдем производную функции .

Теперь выразим из данного решения произвольную постоянную С , для этого пропотенцируем его, получаем , подставим её в дифференциальное уравнение: .

3. Уравнение с разделяющимися переменными

Рассмотрим виды уравнений, решения которых находятся всегда в конечном виде. Среди таких уравнений наиболее простыми являются уравнения с разделяющимися переменными. В свою очередь уравнения с разделяющимися переменными разбиваются на отдельные случаи уравнений.

I случай: . Уравнение не содержит искомой функции . Непосредственно получаем, что его решением будет . Областью существования такого решения является промежуток , где определена и непрерывна функция . Особого рассмотрения требуют точки разрыва функции . Если число является точкой разрыва II рода, то может быть решением перевернутого уравнения . С геометрической точки зрения это значит, что прямая будет интегрируемой кривой. Однако в этом случае может оказаться, что через точки этой интегральной кривой проходит еще одна интегральная кривая. Вся совокупность решений будет складываться из решений вида и .

Примеры: 1) .

Найдем область существования решения уравнения: , отсюда .

Проинтегрируем уравнение: .

Рассмотрим значение , подставим его в перевернутое уравнение , получим , т.е. верное равенство, значит, решение уравнения.

Ответ: и .

2)

Проинтегрируем уравнение: . Проверим значение , получим , т.е. верное равенство.

Ответ: и .

II случай . Уравнение не содержит явно независимой переменной . Допустим, что на сегменте , тогда уравнение запишем в виде . Получаем уравнение рассмотренного ранее случая 1 по отношению к переменной . В результате получаем .

Значение , при котором , так же является решениями данного уравнения. Это решение может быть особым, т.е. в каждой или в отдельных точках нарушается свойство единственности интегральной кривой, проходящей через эту точку.

Пример: .

.

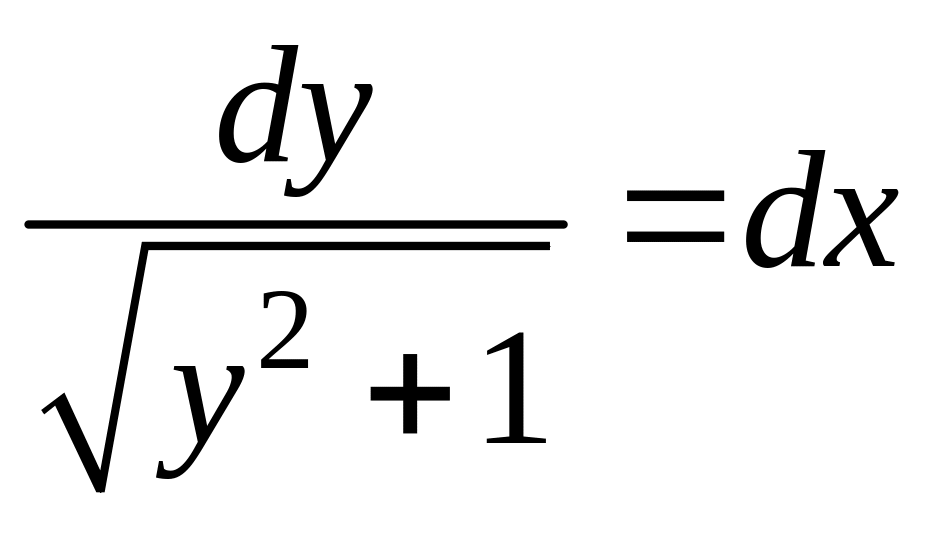
Запись решения в таком виде называется общим интегралом.

III случай .

Общим интегралом того уравнения, называемого уравнением с разделенными переменными находятся по формуле: .

Пример: .

.

IV случай .

Разделим левую и правую части уравнения на произведение , считая, что это произведение . Получаем:

.

Получили уравнение с разделенными переменными. Особого рассмотрения требуют значения, при которых и .

Уравнение с разделяющимися переменными можно записать так же и в виде:

,

тогда для его интегрирования так же собираем выражения, содержащие переменную в одной стороне, а в другой – , т.е. переменные и разделяются. При разделении переменных надо следить за тем, что бы дифференциалы и всегда находились в числителе. В результате получаем: ,

.

Особого рассмотрения требуют значения , при котором .

Пример: .

,

.

1) .

Подставим эти значения в уравнение: .

2) , подставляем в уравнение: .

Ответ: , , .