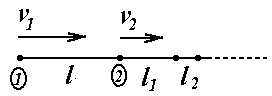Ход работы

1. Изложите своими словами ход рассуждений Зенона в данной апории и логический вывод, который следует в их результате.

2. Попытайтесь привести свои соображения в опровержение этого парадокса. При необходимости обратитесь за разъяснениями к преподавателю.

3. Поскольку со времени Зенона всем, кто знакомится с этой апорией, очевидна абсурдность вывода, неоднократно предпринимались попытки вскрыть противоречия или даже ошибки в самих рассуждениях Зенона. Строго говоря, парадокс необходимо преодолеть, не выходя за рамки приводимых в нем доказательств. Поэтому изобразите схематически последовательность взаиморасположений исследуемых объектов и рассмотрите некоторые исторически известные “опровержения”.

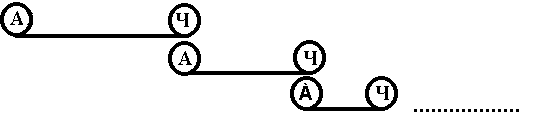
А. В рассуждениях апории не учитывается конечность размеров движущихся объектов. Между тем на определенном этапе неизбежно возникнет соприкосновение объектов.

Б. Зенон безосновательно допускает бесконечную делимость расстояния на все более мелкие отрезки. Между тем, может существовать предел делимости пространства, что автоматически означает соединение объектов, находящихся на минимальном расстоянии. (Возражение Аристотеля, в настоящее время дополняемое рассуждениями о “кванте” пространства).

В. В рассуждениях апории не затрагивается определение понятия “догнать”. Так как находиться в одной точке пространства два объекта не могут, то они всегда будут в пространстве разнесены. Поэтому, указав некоторые наперед заданное малое расстояние между объектами, момент его достижения и следует считать “до­гонкой”. (Разъяснения А.Грюнбаума в 50-х годах ХХ в.).

4. Проанализируйте вышеприведенные аргументы и обоснуйте, что с чисто логических позиций они не могут считаться опровержениями парадокса Зенона.

5. Внимательно изучите математическое представление апории Зенона, базирующееся на элементарных знаниях механики и математики в пределах курса средней школы.

Пусть скорость одной материальной точки равна , второй – , причем . Hачальное расстояние между точками равно l, скорости направлены в одну сторону. Hайдем последовательно отрезки l₁, l₂ и т.д., которые будет проходить первая точка по мере движения за второй.

а) б)

в)

Определим сумму отрезков пути, пройденных первой точкой:

Упростим выражения, введя отношение скоростей:

Выражение в скобках представляет сумму членов убывающей геометрической прогрессии со знаменателем . При бесконечном увеличении числа отрезков прогрессия становится бесконечно убывающей. Hайдем сумму бесконечного числа отрезков:

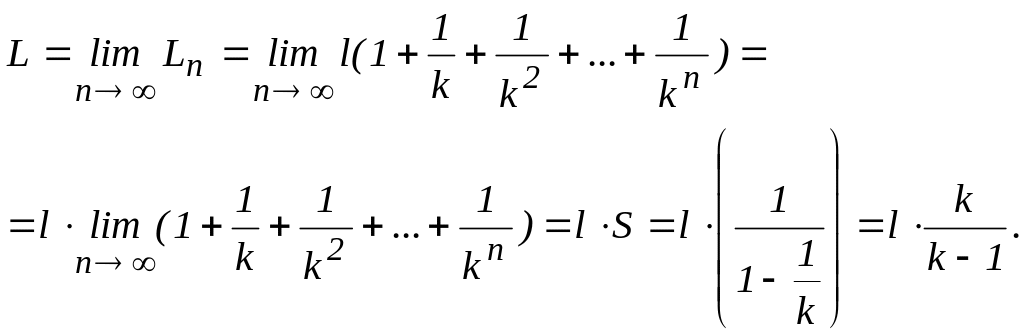
Здесь использована формула суммы бесконечно убывающей прогрессии:

где ₀ – первый член прогрессии, q – знаменатель прогрессии.

6. Проанализируйте полученное выражение. Учитывая, что l и k – величины конечные, величина L получается конечной. То есть, несмотря на бесконечное число этапов перемещения, первая точка догонит вторую точку на конечном расстоянии L за конечный промежуток времени

7. Убедитесь, что полученный строго математически результат, тем не менее, логически не опровергает апорию Зенона. Для этого постройте график функции для последовательных этапов перемещения первой точки. Фактически, это график дискретной функции:

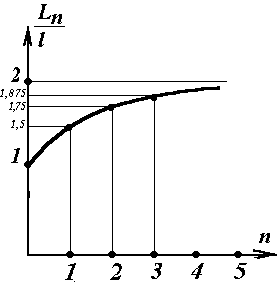
0	Величину k удобно взять небольшой (k=2 или k=3 и т.п.), а n – не превышающим 5–10. Здесь дан пример графика для k=2.

Можно видеть, что величина функции бесконечно прибли­жается к своему пределу , но никогда не достигает его.

Таким образом, осуществленный предельный переход от переменной суммы конечного числа слагаемых к постоянной величине предела является математически условным и логически не обоснованным.

Резюме

В рамках строго логических построений (т.е. придерживаясь правил формальной логики) апория Зенона “Ахиллес быстроногий” является на сегодняшний день неопровержимой. Это доказывает, что в поисках истинных знаний об окружающей действительности одних логико-математических методов недостаточно, ибо они, как и все остальные методы познания, огрубляют окружающий мир при отражении в нашем сознании.

Контрольные вопросы

1. Перечислите названия трех остальных апорий Зенона и изложите их своими словами.

2. Может ли величина k быть не целой?

3. Может ли величина k  ? Ответ поясните.

Литература

1. Волков Г. У колыбели науки. М.: Молодая Гвардия, 1971. – С. 147–159.

2. Чудинов Э.М. Пространство и время в современной физике. М.: Знание, 1969. – С. 39–41.

3. Кондаков H.И. Логический словарь. М.: Hаука, 1976. (Статья “Апория”).

Практическая работа № 9

ЗАКОНОМЕРНОСТИ РАЗВИТИЯ НАУЧНЫХ ТЕОРИЙ

Часть 1

Раздел программы: Теоретические методы познания.

Необходимые предварительные знания: Тригонометрические функции. Измерение углов в круге.

Теоретическая часть

Теоретические методы познания составляют важную часть естественнонаучной методологии. Наивысший уровень теоретического осмысления изучаемых явлений обеспечивают научные теории. В точных науках они характеризуются высшей степенью математизации. Среди совокупности функций научной теории основными выступают: описание известных опытных фактов, их объяснение (т.е. выяснение причин) и предсказание неизвестных эмпирических результатов. Кратко их можно обозначить как функции обоснования и предвидения. Hаучное познание – процесс сложный и противоречивый, обусловленный многоплановым взаимодействием объективного материального мира и мыслящего субъекта – ученого. Поэтому научные теории претерпевают сложный процесс эволюции, включающий этапы зарождения теорий, их становления, развития и отмирания. Последний этап характеризуется либо заменой прежней теории на кардинально новую (научная революция), либо разной степенью перестройки этой теории. В эволюционном процессе научной теории действуют определенные закономерности и проявляются характерные особенности. Некоторые из них будут изучаться в данной теме на примере эволюции системы мира (теоретической космической модели).