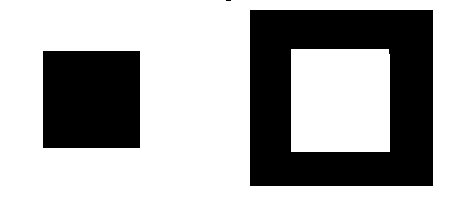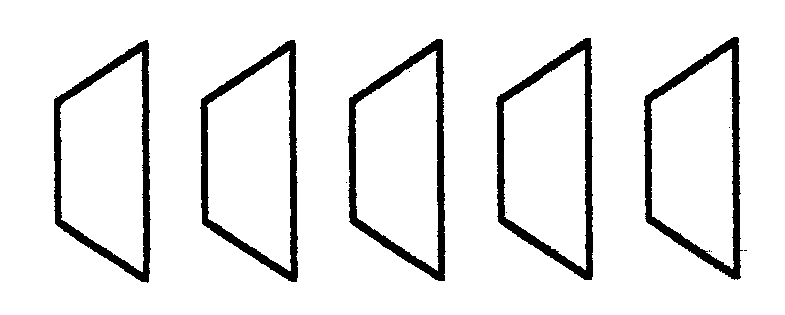Контрольные вопросы

1. Можно ли полностью исключить случайную погрешность при измерениях и обработке результатов?

2. Может ли приборная погрешность конкретной линейки быть меньше рассчитанной в работе? Ответ обоснуйте.

3. Имеются ли в проделанных в работе измерениях длины математически не учтенные ошибки и почему ?

4. Приведите примеры случайной приборной и систематической индивидуальной погрешностей при измерениях линейкой ?

Литература

1. Фетисов В.А. Оценка точности измерений в курсе физики средней школы. М.: Просвещение, 1974. – 96 с.

2. Деденко Л.Г., Керженцев В.В. Математическая обработка и оформление результатов эксперимента. М.: МГУ, 1977. – 114 с.

3. Берков В.И. Технические измерения. М.: Высшая школа, 1983. – 144 с.

4. ГОСТ 427-75. Линейки измерительные металлические. М.: Изд-во стандартов, 1986. - 12 с.

Практическая работа № 7 искажения восприятия действительности

Разделы программы: Естествознание в Древней Греции. Естествознание в эпоху капитализма. Методология научного познания.

Необходимые предварительные знания: Искажения зрения (не­достатки оптической системы глаза), строение и работа зрительного анализатора.

Теоретическая часть

Ученым Древней Греции уже было известно о том, что “не­пос­редственное” восприятие окружающего мира производится посредством органов чувств, и что этими органам свойственны искажения восприятия. Платон изложил это знание в форме аллегории “Театр теней”, приводящей к выводу о возможности истинного познания действительности. В Hовое время другой философ, И.Кант, исходя из тех же предпосылок, сделал противоположный вывод, назвав действительный мир “вещью в себе”. Hа данном занятии ставится цель убедиться в искажениях восприятия на примере зрительного анализатора, обеспечивающего переработку более 90 % информации, поступающей человеку через внешние органы чувств, а также – в возможности коррекции искажений посредством дополнительных методов познания и прие­мов исправления.

Ход работы

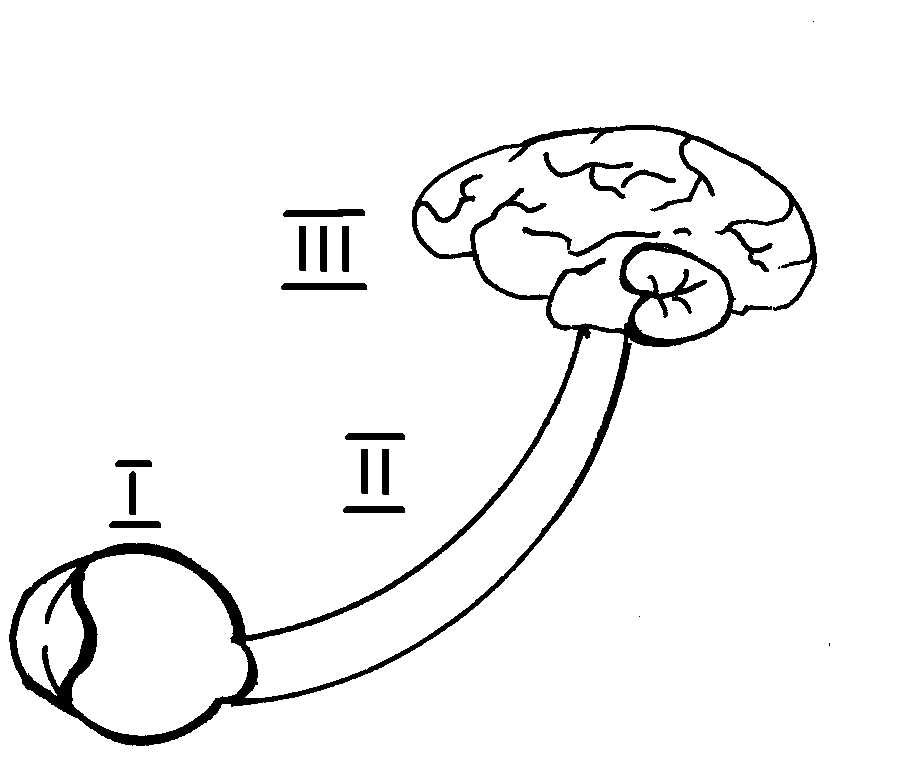
1. Зарисуйте схему строения зрительного анализатора (см. рис.). Отвлекаясь от его структурно-функционального единства, выделите три звена: “физическое” (I), “физиологическое” (II) и “психологическое” (III).

Далее в работе будут рассматриваться отдельно искажения, обусловленные преимущественно деятельностью каждого из звеньев.

2. Рассмотрите физические искажения, обусловленные недостатками оптической системы глаза. Для этого схематически постройте ход лучей при получении изображения предмета в оптически нормальном глазе. Укажите оптическую ось, оптический центр, одинарные и двойные фокусные расстояния, расположения предмета и его изображения. Затем постройте изображение при близорукости. С помощью рассеивающей линзы скорректируйте ход лучей и получающееся изображение. Затем проделайте аналогичные построения для дальнозоркости и скорректируйте их с помощью собирательной линзы. Проанализируйте полученные результаты и запишите в протокол общий вывод.

3. Рассмотрите физиологические искажения, проведя соответствующие построения.

а) Опыт Мариотта.

(Поперечные размеры фигур 5–10 мм, расстояние между их центрами – 50 мм, правым глазом смотреть по центру на левую фигуру).

Объясните результат и запишите вывод в протокол.

б) Опыт “перпендикуляр”.

1) нарисуйте указанную фигуру “на глаз”, добиваясь равенства длин вертикальной и горизонтальной линий, опыт лучше выполнить на нелинованной бумаге размером 100х100 мм ориентировочно; 2) измерьте линейкой длину и ширину фигуры (можно округлить результаты до 1 мм) и запишите в тетрадь; 3) запишите в протокол вывод об искажении восприятия соотношения длин вертикальных и горизонтальных линий.

Причиной является несовпадение углов раскрытия поля зрения по вертикали и горизонтали. Аналогичный эффект достигается при зарисовывании “цилиндра” (головного убора).

Примечание: Для студентов художественно-графических факультетов (в том числе архитектурных) предлагается зарисовать “на глаз” классную доску и проверить соотношение размеров.

в) Опыт “квадраты”.

(Два квадрата одинаковых раз­меров зарисовываются на контрастном фоне, размеры сторон квад­ратов 15–20 мм).

Сделайте вывод и запишите в протокол.

Причину эффекта, названного “иррадиацией”, древние греки усматривали в “неправильном ощупывании” выходящими из глаза лучами-щупальцами светлых предметов. Термин современной наукой сохранен, однако в действительности причиной иррадиации для светлых объектов является передача физиологического возбуждения с освещенных участков сетчатки на соседние, самим изображением на освещенные.

4. Рассмотрите психологические искажения, являющиеся самыми многочисленными и наиболее выраженными из всех.

а) ”Отверстие в ладони”.

Из тетрадного листка сверните трубочку и приставьте вплотную к правому глазу, смотря им через нее. Левую руку, раскрыв ладонью к себе, расположите у дальнего конца трубки, касаясь ее сбоку, и смотрите на ладонь левым глазом. Выявите получившуюся иллюзию и запишите результат в тетрадь. Причиной иллюзии является “негативная галлюцинация” – психологическое исключение из зрительного образа изображения части ладони, накладывающегося на “прозрачное” поле зрения в трубке.

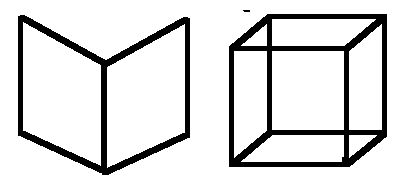
б) “Колеблющаяся” книга и “колеблющийся” куб.

Зарисуйте изображенные фигуры и выясните характер иллюзии. Вто­рая фигура так­же назы­вается “куб Неккера” (по имени ученого).

в) “Прямоугольники со стрелками”.

(Оба прямоугольника имеют одинаковые раз­меры, например, 10х20 мм). Отметьте эффект, объясните его и запишите вывод в протокол.

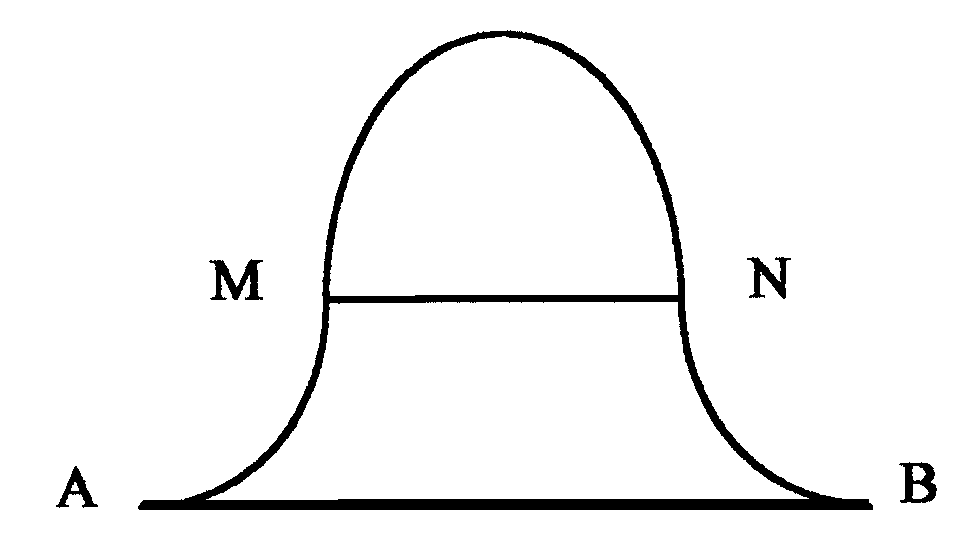
г) “Гауссиана”.

1) После построения колоколообразной кривой с длинны­ми нижними усами проведите на глаз секущую MN так, чтобы ее длина составляла половину АВ. 2) Измерьте линейкой действительные размеры и запишите в тетрадь, сделайте вывод.

Иллюзия объясняется мысленным неучетом концов “усов” у основания криволинейной трапеции AMNB.

д) “Трапеции”.

Нарисуйте 5–6 одинаковых тра­пеций в указанном взаиморасположении. Размеры оснований трапеций удобно взять 10 и 20 мм, между основаниями - 10 мм, а расстояния между трапециями – 5 мм.

Объясните полученную иллюзию, попытайтесь дать ей объяснение.

Примечание: Дополнительные иллюзии, требующие сложных построений, могут быть продемонстрированы из источников литературы по нижеприведенному списку.

Резюме

Органам чувств присущи искажения восприятия действительных объектов окружающего мира. Однако, с применением дополнительных методов познания и корректирующих методик влияние искажений на познание может быть скомпенсировано или исходно устранено.

Контрольные вопросы

1. В чем заключается аллегория “Театр теней” ?

2. Какие оптические искажения глаза, кроме рассмотренных, возможны и как они корректируются?

3. Почему “книга” и “куб” названы “колеблющимися” ?

4. Пользуясь литературой из списка, придумайте новые иллюзии в соответствии с изложенными принципами.

Литература

1. Демидов В. Как мы видим то, что видим. М.: Знание, 1989. – С.165–179.

2. Воронин Л.Г. и др. Физиология высшей нервной деятельности и психология. М.: Просвещение, 1977. – С. 136–146.

3. Фомин С.В., Беркенблит В.М. Математические проблемы в биологии. М.: H., Физматгиз, 1973. – С. 124–145.

4. Голицын Г.А., Петров В.М. Гармония и алгебра живого. М.: Знание, 1990. – С. 69–80.

Практическая работа № 8

ЛОГИКО-МАТЕМАТИЧЕСКИЕ ПОДХОДЫ В НАУКЕ

Разделы программы: Естествознание в Древней Греции. Методология научного познания. Роль математики в науке.

Необходимые предварительные знания: Начальные сведения по теории математических пределов. Геометрические прогрессии.

Теоретическая часть

Древнегреческий философ Зенон Элейский в V в. до н.э. сформулировал ряд научных парадоксов-апорий, из которых до нас в изложении Аристотеля дошли только четыре. Самая известная из них – “Ахиллес быстроногий” (“Ахиллес и черепаха”). В ней логически обосновывается, что самый быстроногий герой не догонит самого медлительного существа, если изначально между ними будет задан запас расстояния. Этот парадокс в настоящее время имеет отнюдь не только историческую значимость, но и является своего рода оселком в обучении логике, в умении прилагать новые достижения физики и философии к решению конкретных модельно-теоретических задач. Со времени Зенона метод парадоксов успешно используется в разных науках (не только естественных) с целью стимулирования решения важных научных проблем.