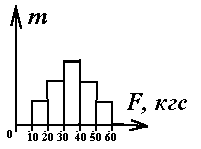Контрольные вопросы

1. Как можно сравнивать результаты статистической обработки опытных данных для разных групп студентов и какие выводы можно сделать из этого?

2. Hайдите величину b/a и ответьте, почему в науке а/b обозначается  (“фи малое”), а b/a –  (“фи большое”)? Как они связаны между собой?

3. Изучите, используя нижеуказанную литературу, значение “золотой пропорции” в природе, науке и искусстве (задание на дом).

4. Что такое числа, или ряд Фибоначчи ? Как он конструируется? Как он связан с золотой пропорцией?

Литература

1. Волошинов А.В. Математика и искусство. М.: Просвещение, 1992. – С. 204–207.

2. Сонин А.С. Постижение совершенства. М.: Знание, 1987. – С.137–179.

3. Петров В.М., Прянишников H.Е. Формулы прекрасных пропорций. М.: Знание, Естественнонаучный ф-т, вып.2, 1970. – C. 72 – 92.

Практическая работа № 4

МАТЕМАТИКА И СПОРТ

Раздел программы: Роль математики в науке.

Необходимые предварительные знания: Начала математической статистики.

Теоретическая часть

В настоящее время подготовка спортсменов высокой квалификации обязательно включает использование новейших достижений самых различных наук: медицины, биохимии, биомеханики, общей биологии и т.д. Важная роль в этом комплексе принадлежит математическим наукам: теориям вероятности и информации, кибернетике, исследованию операций, теории игр, математической статистике и т.д. В данной работе на учебном примере демонстрируется одно из направлений математизации спорта – применение статистики в спортивном нормировании.

Ход работы

Примечание: Занятие обязательно проводится для студентов факультетов физической культуры и спорта, сфор­мированных в учебные группы по половозрастному признаку. Необходимой принадлежностью работы является ручной (кистевой) динамометр (“сило­мер”).

1. Измерьте силу кисти правой и левой рук в положении стоя. Сообщите свои результаты преподавателю. Поскольку силомер проградуирован в килограммах силы (кгс), что метрологическим стандартом не предусмотрено, эти результаты являются нестандартизированными (используются как исключение). Показания снимите с точностью (округлением) до 1 кгс.

2. Запишите попарно все результаты для правой (F_пр) и для левой (F_лев) рук, полученные студентами группы. Сделайте вывод о силовом преимуществе одной из рук и определите надежность такого заключения. Для этого подсчитайте число случаев с преобладанием величины силы для одной руки – правой или левой [N⁽⁺⁾], затем – число случаев, где показания рук совпадают [N⁽⁰⁾]. Воспользуйтесь таблицей пограничного значения (надежность 95%) критерия знаков (библиография [1]).

N(+) +N(0)	10	11- -12	13	14- -15	16- -17	18	19- -20	21	22- -23	24- -25	26	27- -28	29- -30	31
N(+)	9	10	11	12	13	14	15	16	17	18	19	20	21	22

3. Затем сделайте вывод о преимущественном силовом развитии правой руки (т.е. о преобладании в массе правшей). Для этого воспользуйтесь вышеуказанной таблицей, однако случаи равенства показателей обеих рук исключите из рассмотрения. При оценках вместо N⁽⁺⁾ учитывайте N⁽⁺⁾_пр (т.е. превалирование правой руки), а вместо N⁽⁰⁾ учитывайте N⁽⁺⁾_лев (превалирование левой руки). Сделайте вывод.

4. Составьте вариационный ряд (F_min –F_max) силовых показателей рук всех студентов группы, используя только предпочтительные результаты (для правшей – по правой руке, для левшей – по левой руке), и постройте гистограмму их распределения.

0 10 20 30 40 50 60

По оси ординат откладываются числа случаев (студентов).

5. Проведите простейшую статистическую обработку полученных результатов, т.е. найдите:

а) среднее значение: n – общее число результатов,

б) среднее квадратическое отклонение: .

Для приближенной ускоренной оценки последнего показателя можно использовать таблицу 2 из того же литературного источника. Результаты расчетов округлите до единиц кгс.

6. Воспользуйтесь теоретическими результатами для нормального (гауссовского) распределения P(x) случайных величин x, а именно – интервалов последней, включающих основную часть встречающихся значений (P – вероятность):

К=1 соответствует 68,3 % результатов, К=2 соответствует 95,5 % результатов, К=3 соответствует 99,7 % результатов.

Найдите значения указанных стандартных интервалов (К=1,2,3). Например, для К=1 – интервал F: 34–56 кгс.

7. Определите окончательные (нормативные) интервалы силы кисти, присвоив им соответственную экспертную оценку в баллах:

– 3_F ÷ – 2_F  1 балл,

– 2_F ÷ – _F  2 балла,

– _F ÷ + _F  3 балла,

+ _F ÷ + 2_F  4 балла,

+ 2_F ÷ + 3_F  5 баллов.

Результаты расчетов занесите в протокол.

Резюме

Методы математической статистики являются эффективным способом проектирования спортивных квалификационных нормативов.

Контрольные вопросы

1. Как следует поступать при разбиении интервалов встречаемости величин, чтобы одно и то же значение не попадало строго на их границу ?

2. Можно ли предложить другой экспертный подход для определения интервалов и балльных оценок? Обоснуйте ответ.

3. Укажите (по литературным источникам) конкретные применения математики в спорте (по видам спорта и целям) – задание на дом.

Литература

1. Ашмарин И.П. и др. Быстрые методы статистической обработки и планирование экспериментов. Л.: ЛГУ, 1971. – С. 7–24.

2. Садовский Л.Е., Садовский А.Л. Математика и спорт. М.: H., Физматгиз, 1985 ( б-ка “Квант”, вып. 44). – 192 с.

Практическая работа № 5

ОСНОВЫ МЕТРОЛОГИИ

Часть 1

Разделы программы: Роль метрологии в науке. Основные положения метрологии.

Необходимые предварительные знания: Система единиц измерений СИ.

Теоретическая часть

Метрология – учение об измерениях – играет важную роль в научном познании и практической жизни. Отец русской метрологии Д.И. Менделеев (выдающийся химик) провозглашал: “Hаука начинается с тех пор, как начинают измерять, точная наука немыслима без меры.” Очевидность этого утверждения вытекает из роли измерения как основы количественного опыта. В практической жизни, а именно – в народнохозяйственной деятельности, метрология играет важнейшую роль в стандартизации продукции (работ, услуг), т.е. определяет важные стороны общественной жизни. Особенно велика роль метрологии в процессах сертификации при рыночной экономике.