Контрольные вопросы
Возможно ли округление точных чисел?
Можно ли указать однозначное правило округления с поправкой, если отбрасывается единственная цифра 5, примыкающая к округляемому разряду? Обоснуйте ответ.
Как следует правильно поступать в расчетах, если приближенное число делится на точное, причем в последнем число значащих цифр меньше, чем в первом?
Можно ли при действиях с приближенными числами пользоваться электронным калькулятором? Обоснуйте ответ.
Литература
Деденко Л.Г., Керженцев В.В. Математическая обработка и оформление результатов эксперимента. М.: МГУ, 1977. – С. 100–103.
Фетисов В.А. Оценка точности измерений в курсе физики средней школы. М.: Просвещение, 1974. – С. 15–25.
Практическая работа № 3
МОДЕЛИРОВАНИЕ ГАРМОНИИ
Разделы программы: Естествознание в Древней Греции. Естествознание в эпоху Возрождения. Математическое моделирование.
Необходимые предварительные знания: Начала математической статистики.
Теоретическая часть
По современным научным концепциям, нынешние формы материальной организации (включая живые структуры) являются продуктами эволюции Вселенной. Возникновение человеческого общества, разума, культуры и их эволюции также с необходимостью включают эволюцию материального мира (природы). Поэтому в системе природы, общества, культуры, психики и разума действуют единые законы (хотя и имеются особые закономерности в каждой области). Одним из таких универсальных законов, давно открытых человечеством, является закон гармонии и красоты.
Ход работы
Примечание: Занятие проводится в обязательном порядке для студентов факультетов искусств и психологии и отделений естествознания. Исходный чертеж выполняется на нелинованном листе бумаги предпочтительно квадратной формы (например, 200х200 мм).
1. Начертите на листе бумаги прямоугольник с соотношением сторон, формирующих наибольшее эстетическое восприятие.
2. Измерьте миллиметровой линейкой его ширину “a” и длину “b” (a<b) и запишите в протокол работы.
3. Hайдите отношение а/b с точностью до трех значащих цифр, запишите его в протокол и сообщите преподавателю полученный результат.
4. Все полученные группой результаты в совокупности запишите в тетрадь. Постройте гистограмму полученных результатов. В большинстве случаев они оказываются распределенными в интервале 0,3 – 0,9. Обратите внимание, что, несмотря на разнообразие эстетических вкусов, в распределении результатов проявляется определенная закономерность: они группируются в средней части интервала и реже встречаются у его краев.
|
По оси ординат откладываются числа случаев, соответствующих интервалам х.
|
5. Произведите простейшие статистические расчеты (первый уровень математизации), определив:
а)
среднее значение:
;
n – общее
число результатов;
б)
среднее квадратическое отклонение:
;
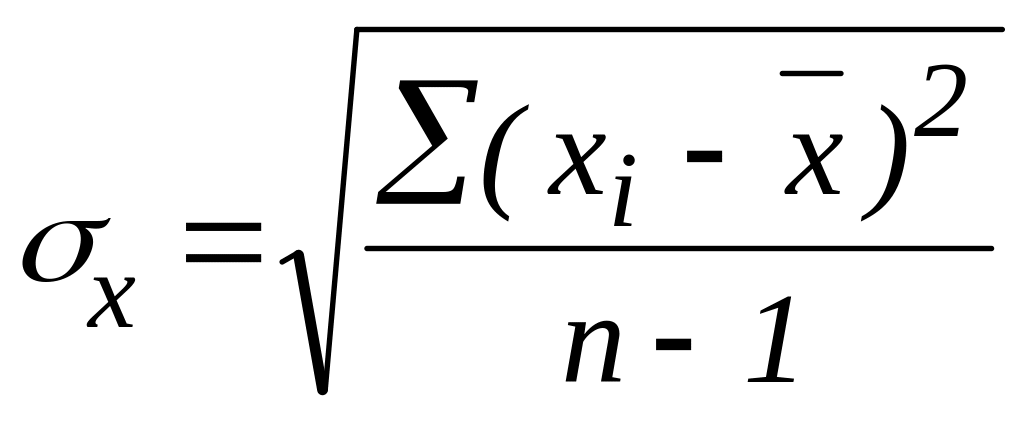в)
коэффициент вариации:
;
г)
вероятностный интервал для 95
%-го уровня надежности включения
результатов:
.
Результаты округляйте до трех значащих цифр.
Hапример:
Сравните опытный интервал вариации (т.е. хmin – xmax) с расчетным для надежности 95 % и сделайте выводы.
6. Рассчитайте математическую модель (второй уровень математизации), исходя из закономерностей, известных как в Древней Греции (по Пифагору – “золотая пропорция”), так и в эпоху Возрождения (по Леонардо да Винчи – “золотое сечение”).
.
Отсюда, путем решения уравнения, находим
Эта
закономерность известна в математике
как правило деления отрезка “в среднем
и крайнем отношении”. Сравните среднее
значение из опытных данных
,
а также крайние значения (хmin,
xmax)
с рассчитанным по модели значением х.
Сделайте выводы.
Резюме
Математическая модель “золотой пропорции”, получившая опытное подтверждение на протяжении многих столетий, хорошо описывает объективную закономерность гармонии. В настоящее время “золотая пропорция” обнаружена в строении многих природных объектов, в психологии восприятия и находит применение в произведениях искусства и многих других областях