Контрольные вопросы

1. Какие теоретические утверждения в системах мира Пифагора и Евдокса носили чисто описательный характер и не были объяснены с позиций причинной обусловленности?

2. Какими опытными фактами небесной механики не располагали древние греки, в связи с чем такие аспекты не находили отражения в их теориях?

3. Что необходимо было дополнительно проделать Аристарху и его последователям, чтобы гелиоцентрическая система мира была признана научным сообществом?

Литература

1. Климишин И.А. Астрономия вчера и сегодня. Киев: “Наукова думка”, 1977. – 252 с.

2. Силк Дж. Большой взрыв. М.: Мир, 1982. – С. 18–23.

3. Вильвовская А.В. Человек и космос. М.:H., 1994. – С. 32–47.

4. Ильин В.В. Структура и развитие научных теорий. М.: МГУ. 1980. – 82 с.

5. Зигель Ф.Ю. Астрономы наблюдают. М.: Н., Физматгиз, 1977. – 192 с.

Практическая работа № 10

ЗАКОНОМЕРНОСТИ РАЗВИТИЯ НАУЧНЫХ ТЕОРИЙ

Часть 2

Раздел программы: Теоретические методы познания.

Необходимые предварительные знания: Часть 1 данной темы.

Теоретическая часть

Развитие любой научной теории происходит как эволюционным, так и революционным путем. Революционный путь, представляющий собой ломку предыдущей теории, скачкообразную замену ее на кардинально новую, в том числе - диаметрально противоположную, реализуется только на определенном этапе эволюционного развития исходной теории. Для этого этапа характерна невозможность или чрезвычайная трудоемкость теоретического описания и объяснения новых эмпирических данных, т.е. состояние научного кризиса. Революционная теория отнюдь не обязательно должна отвечать на все поставленные научным развитием вопросы, она может в ряде аспектов уступать прежней теории. Однако в совокупности своих возможностей (объяснение известных фактов, упрощение теоретических построений и расширение возможностей предсказания новых фактов) новая теория должна обязательно превосходить старую. Тогда она принимается научным сообществом, несмотря порой на ее необычность и даже “дикость”.

Ход работы

1. Известный греческий астроном и математик Гиппарх Никейский (190-125 гг. до н.э.) занимался особенно тщательными измерениями движения Солнца и Луны, а также других планет и звезд. Им было открыто много опытных фактов, не объясняемых в рамках модели гомоцентрических сфер. В том числе - неравномерность вращения Солнца и Луны по небосводу. Поэтому Гиппарх сместил положения центров круговых орбит Солнца и Луны относительно центра Земли. Такие орбиты были названы эксцентрами.

Hарисуйте эксцентр, укажите позицию Земли и обоснуйте неравномерность видимого вращения светила при наблюдении с Земли.

2. Благодаря работам Гиппарха астрономы отказались от модели хрустальных сфер, а перешли к более продуктивным описаниям движений планет с помощью не только эксцентров, но и эпициклов и деферентов, предложенных еще до Гиппарха астрономом Аполлонием Пергским ( 250-205 гг. до н.э.). Классическую форму теории эксцентрических движений разработал великий астроном и математик Клавдий Птолемей (90-160 гг. н.э.) из Александрии. Эта теория просуществовала почти 1,5 тысячелетия , превосходно выполняя все свои функции. Она и сейчас используется, но уже не в астрономии, а в практической геодезии, топографии, строительстве и т.п., т.е. в земных масштабах. Следует также учесть, что во времена Птолемея астрономы уже располагали достаточно точными приборами (армилла, квадрант и др.). Для описания движения планет Птолемей использовал эксцентры Гиппарха, эпициклы и деференты Аполлония и добавил конструктивную точку, позже названную эквантом, т.е. “вырав­ни­вающей точкой”.

Зарисуйте основные элементы системы Птолемея, используемые для описания планетарных движений.

Р-планета, Эп-эпицикл, Д-деферент (эксцентр), О-центр деферента, З-Земля, Эк-эквант.

Центр эпицикла движется по окружности деферента нес­колько неравномерно, равномерное его движение происходит от­носительно экванта. Таким образом, система Птолемея позволяла легко объяснять петлеобразное, видимое с Земли, движение планеты с помощью совокупности всего двух простых движений - вращения совместно с эпициклом и обращения вдоль деферента.

Изобразите, используя данный чертеж, траекторию движения планеты, допуская, как у Птолемея, что центр эпицикла движется по деференту. Полученная кривая линия называется эпициклоидой. Объясните, в чем выражалось преимущество системы Птолемея в объяснении петлеобразного движения планет (в сравнении с моделью гомоцентрических сфер Евдокса - Аристотеля), кроме ее простоты.

3. В чисто описательном плане система мира Птолемея имела настолько разительные преимущества (в том числе - в точности предсказания положения планет на небе на столетия вперед), что именно ее стали позднее ассоциировать с геоцентризмом, упуская из вида, что, как и любая совершенная теория, она является продуктом эволюционного теоретического развития. Гибкость системы Птолемея в ее адаптации к новым опытным фактам заключалась в возможностях уточнять или радиус деферента, или скорость обращения и радиус эпицикла, или эксцентриситет Земли. И, в особенности, можно было добавлять к каждому эпициклу последовательность новых эпициклов уменьшающегося радиуса таким образом, что каждый предыдущий выступал в роли деферента для последующего. И если для Луны и Солнца Птолемей обошелся только принципом эксцентров Гиппарха, то для остальных пяти светил он использовал 40 эпициклов!

Зарисуйте упрощенную схему системы мира Птолемея и объясните ее действие.

4. Основные параметры своей модели мира Птолемей определил с высокой точностью на столетия вперед. Hо приблизительно через одну тысячу лет (в XII в.) стали заметны расхождения в вычисленных и реальных положениях планет. Так, отклонение Марса от расчетного положения составило 2⁰ (в среднем 7 в год). Пришлось увеличивать число эпициклов, и к середине XVI в. (эпоха Коперника) их число для уточненной геоцентрической системы превышало 70. Такое усложнение схемы Птолемея привело к тому, что эта теория перестала отвечать своим задачам и, фактически, рухнула под собственной тяжестью.

5. Революционная смена системы мира Птолемея было произведена великим польским ученым Николаем Коперником (1473-1543). Это учение было изложено в его книге “Об обращениях небесных сфер”(1543). Он поменял местами Солнце и Землю (с обращающейся вокруг нее Луной), сохранив птолемеевский принцип деферентов, эпициклов (их у Коперника было 48, т.е. больше, чем исходно у Птолемея). Кроме того, Коперник постулировал равномерное движение эпициклов вдоль деферентов, а также - вращение Земли вокруг оси. Таким образом, по своей основной идее система Коперника повторяла систему Аристарха.

Зарисуйте схему гелиоцентрической системы мира Коперника по аналогии со схемой Птолемея на вышеприведенном рисунке.

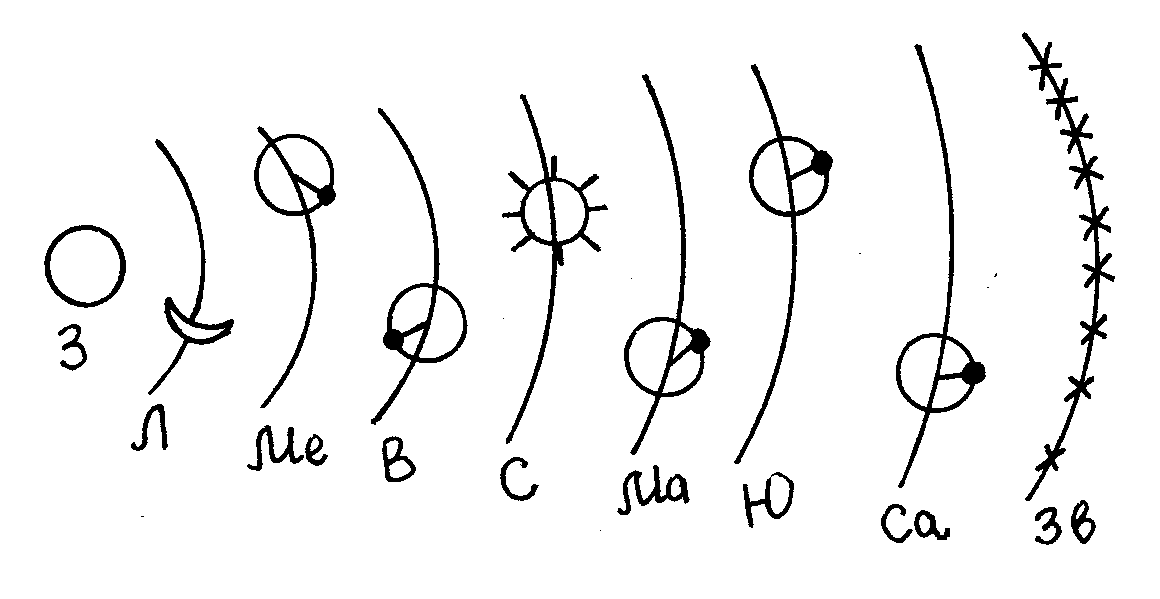
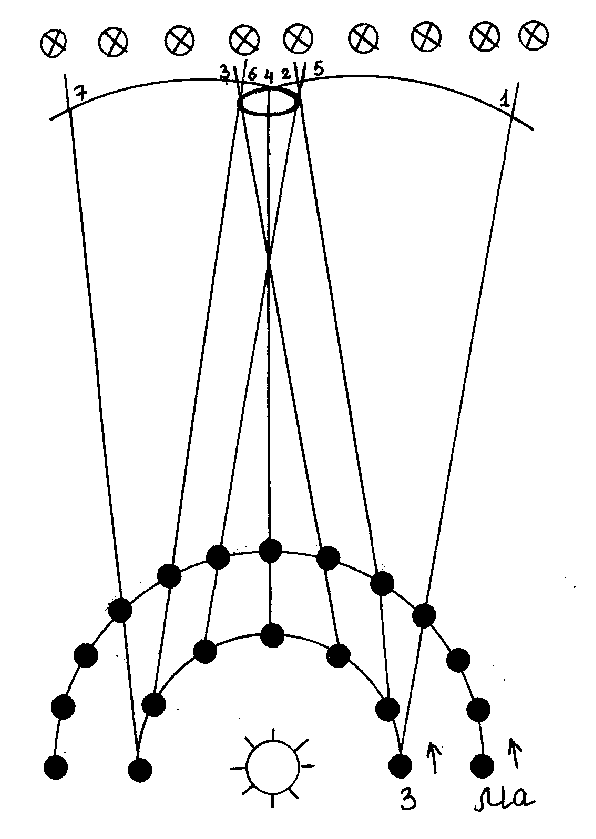
6. Кроме упрощения в описательном плане, модель Коперника позволила объяснить естественным образом возвратное движение планет на небосводе (см. рис.)

Период обращения Мар­са вокруг Солнца превышает период обращения Земли, поэтому в проекции на звездное небо будет наблюдаться петлеобразное движение этой планеты. Перечертите схему в тетрадь и объясните рисунок. Ответьте на вопрос, будет ли петлеобразное движение на фоне звезд наблюдаться для Венеры? Ответ поясните чертежом. Для облегчения его выполнения используйте научные данные о периоде обращения Венеры (примерно 0,6 года).

56