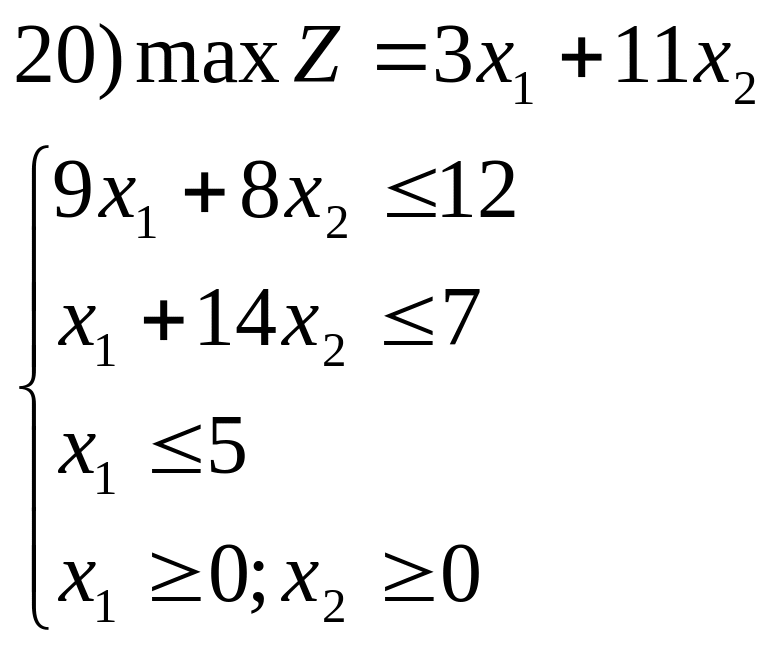Варіанти завдань Задача 1
Підприємство може виготовляти два вида продукції А і В. Випуск цих видів продукції складає відповідно х1 і х2 одиниць.
Прибуток на одиницю продукції складає відповідно С1 і С2 грошевих одиниць.
В розпорядженні підприємства є тільки в1 тисяч машино-годин устаткування, в2 тисяч квадратних метрів складських приміщень і в3 тисяч кіловат-годин електроенергії.
Нехай відомо, що на одиницю продукції А витрачається відповідно а11,а21,а31 потужностей, на одиницю продукції В – а12,а22,а32.
Визначити випуск х1, х2 продукції видів А і В так, щоб прибуток був найбільшим.
Математична модель задачі (ЗЛП) така:
визначити максимум цільової функції (прибутку)
max Z = c1 x1 + c2 x2 при обмеженнях
Розв’язати задачу двома методами : геометричним і симплекс-методом.
В умовах наведеної задачі у підприємства з’явилась можливість реалізувати наявні ресурси (машино-години устаткування, складські приміщення, електроенергія) деякій організації.
Призначити приблизні ціни на ці ресурси у1,у2,у3 формулюючи і розв’язуючи двоїсту ЗЛП з урахуванням вимог обмеженості по ресурсам.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
До змісту
До змісту
Задача 2
Є два підприємства P i Q .
При виділенні підприємству Р х одиниць коштів на рік, підприємство Р забезпечує прибуток f1(x) одиниць і залишок від виділених коштів g1(x) одиниць.
При виділенні підприємству Q y одиниць коштів на рік, підприємство Q забезпечує прибуток f2(y) одиниць і залишок від виділених коштів g2(y) одиниць.
Обом підприємствам виділено на 4 роки а одиниць коштів.
Потрібно розподілити ці кошти між підприємствами Р і Q так, щоб спільний прибуток за весь період був максимальним.
f2=3,5; g2=0,3 a = 2000 |
f2=3,6; g2=0,4 a = 2000 |
f2=3,7; g2=0,5 a = 2000 |
f2=4,1; g2=0,4 a = 1500 |
f2=4,3; g2=0,2 a = 1500 |
f2=4,3; g2=0,5 a = 1500 |
f2=4,7; g2=0,3 a = 1900 |
f2=4,8; g2=0,4 a = 1900 |
f2=4,9; g2=0,5 a = 1900 |
f2=5,5; g2=0,5 a = 1600 |
f2=5,4; g2=0,4 a = 1600 |
f2=5,4; g2=0,5 a = 1600 |
f2=5,1; g2=0,7 a = 1700 |
f2=5,2; g2=0,6 a = 1700 |
f2=5,3; g2=0,5 a = 1700 |
f2=2,9; g2=0,4 a = 1400 |
f2=2,8; g2=0,1 a = 1400 |
f2=2,7; g2=0,3 a = 1400 |
f2=4,3; g2=0,4 a = 1300 |
f2=4,4; g2=0,5 a = 1300 |
f2=4,5; g2=0,5 a = 1300 |
f2=3,7; g2=0,5 a = 1200 |
f2=3,6; g2=0,4 a = 1200 |
f2=3,8; g2=0,4 a = 1200 |
f2=4,1; g2=0,3 a = 1100 |
f2=4,2; g2=0,2 a = 1100 |
f2=4,3; g2=0,3 a = 1100 |
f2=4,2; g2=0,4 a = 1000 |
f2=4,1; g2=0,5 a = 1000 |
f2=4,0; g2=0,5 a = 1000 |
|
|
До змісту
До змісту