Функціональні рівняння Беллмана

Будемо вважати, що початковий Х₀ і кінцевий Х_Т стани системи відомі. Цільова функція має сепарабельний вигляд (тобто сума):

де - цільова функція на і-му етапі.

Потрібно знайти оптимальне управління таке, що визначає екстремум цільової функції при обмеженнях .

Нехай - області визначення задач на останньому етапі, двох останніх і т.д.

Позначимо через відповідно умовно-оптимальні значення цільової функції на останньому етапі, двох останніх і т.д., на к останніх і т.д., на всіх N етапах.

Тоді, починаючи з останнього етапу, отримуємо систему рекурентних співвідношень Беллмана

До змісту

До змісту

Задача розподілу ресурсів

Є два підприємства P i Q . При виділенні підприємству Р х одиниць засобів (коштів, засобів виробництва і т.ін.) на рік, підприємство Р забезпечує прибуток

одиниць і залишок від виділених засобів одиниць;

при виділенні підприємству Q y одиниць засобів на рік , Q забезпечує прибуток одиниць і залишок - .

Обом підприємствам виділено на 4 роки а = 1700 одиниць засобів.

Як потрібно розподілити їх кожен рік між підприємствами, щоб спільний прибуток за весь період був максимальним.

Розв’язання

Поділимо весь період тривалістю в 4 роки на 4 етапи, прийнявши кожний рік за один етап.

Будемо нумерувати етапи, починаючи з першого року, і позначимо через х_к, у_к кошти, які виділяються підприємствам P i Q відповідно, на к-му етапі; тоді (1)

спільна кількість коштів, які застосовуються на к – му етапі, або які залишилися в кінці попереднього (к-1) етапу

(2)

очевидно, що а₁ = а = 1700

Прибуток, який одержують підприємства на к-му етапі, дорівнює

(3)

Але, із (1) випливає, що у_к = а_к – х_к , і тоді прибуток, який одержують підприємства на к-му етапі, дорівнює

(4)

Кількість коштів, які використовуються на к – му етапі, можна виразити рекурентною формулою

(5)

Далі, якщо позначити F_k(a_k) - максимальний прибуток, який одержано на останніх етапах, починаючи з к-го, тобто з розподілу а_к коштів, тоді

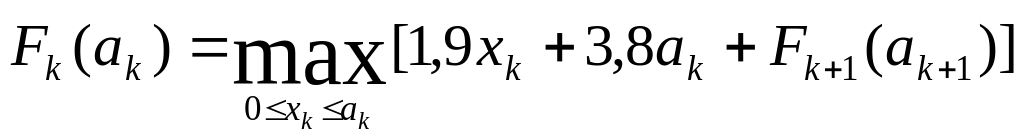(6)

функціональні рівняння Беллмана.

Планування починаємо з останнього етапу.

Для к = 4,3,2,1, застосовуючи формулу (6) для а_к і F_k(a_k), отримуємо, вважаючи, що F₅ = (a₅) = 0 :

К=4 , тобто ,

К=3

,

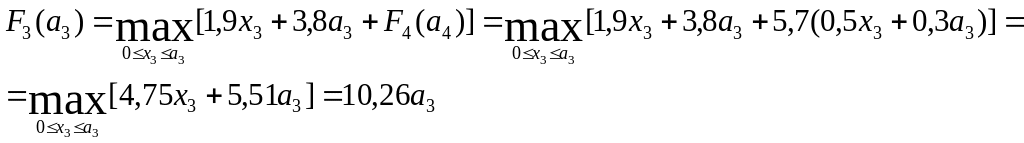тобто .

К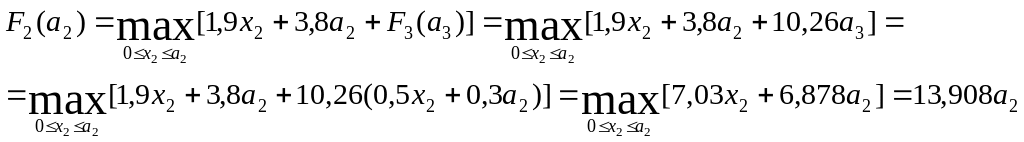 =2

тобто х₂=а₂, у₂=0, а₂= 0,5х₁+0,3а₁ .

К=1

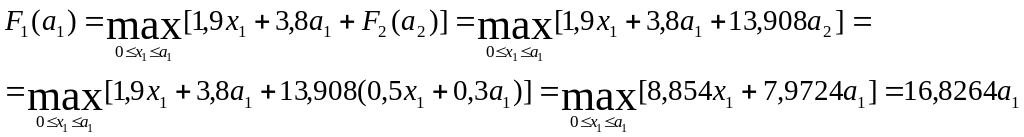
х₁=а_1, у₁=0, F₁(a₁)=16,8264a

процес завершено.

Максимальний прибуток за 4 роки становить

F₁(a₁)=16,8264 a₁ = 16,8264 * 1700 = 28604,88 одиниць.

Для одержання такого прибутка треба в перший, другий, третій і четвертий роки всі кошти віддати першому підприємству

х₁ = а₁ ; у₁ = 0;

х₂ = а₂ ; у₂ = 0;

х₃ = а₃ ; у₃ = 0;

х₄ = а₄ ; у₄ = 0;

а₁ = 1700

а₂ = 0,5х₁ + 0,3а₁ = 0,8а₁ = 0,8*1700 = 1360,

а₃ = 0,5х₂ + 0,3а₂ = 0,8а₂ = 0,8*1360 = 1088,

а₄ = 0,5х₃ + 0,3а₃ = 0,8а₃ = 0,8*1088 = 870,4

залишок коштів становить

а₅ = 0,5 х₄ + 0,3 а₄ = 0,8 а₄ = 0,8 * 870,4 = 696,32 одиниць.

До змісту

До змісту