Пример использования преобразования Фурье

Для иллюстрации вышеизложенного, рассмотрим сигнал меандр с периодом T = 1 с. и пиковой амплитудой A = 1 как показано на рис. 11.

Р ис. 11. Аппроксимация меандра, используя преобразование Фурье. Поскольку ряд Фурье имеет ограниченное количество компонентов, отсюда достаточно плохая аппроксимация

В соответствии с формулами (14)—(16) найдем необходимые коэффициенты:

(21)

(22)

В такой же последовательности находится коэффициенты

(23)

В тех случаях, когда k является нечетным числом, то . Отсюда следует, что при k = 1, 3, 5, … . Когда же k является четным числом, то , следовательно, коэффициенты равны 0. Отсюда можно сделать следующий вывод, если функция — четная², то , если нечетная³, то . Таким образом, функцию, график которой изображен на рис. 11, можно представить в виде ряда Фурье следующим образом:

(24)

В соответствие с формулой (24) гармоники ряда Фурье будут выглядеть, как показано на рис. 12. Каждая гармоника имеет свою собственную частоту, амплитуду и фазу, умноженную на весовой коэффициент. Складывая эти гармонические составляющие, получим аппроксимацию исходной функции, изображенной на рис. 11.

Используя обратное преобразование Фурье, позволяющее преобразовать разложенный сигнал из частотной области обратно во временную область, можно получить исходный сигнал. Однако форма и точность восстановленного сигнал будет зависеть от количества используемых гармонических составляющих. Таким образом, чем больше гармонических составляющих с соответствующими фазами будут задействованы в этом преобразовании, тем более точный получится исходная функция или сигнал.

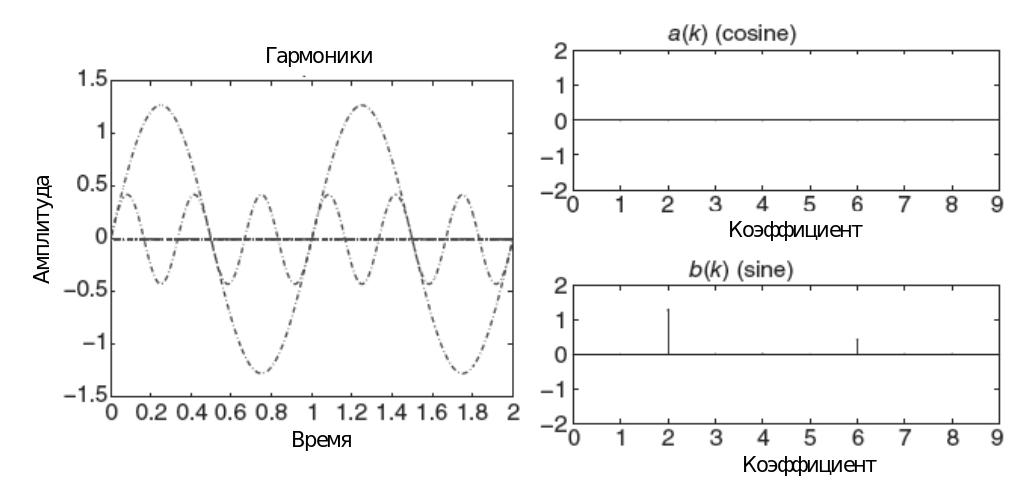
Рис. 12. Разложение в ряд Фурье сигнала меандр

Погрешность приближения

Насколько отличны две функции, можно узнать, измерив расстояние между двумя точками, соответствующими каждой из этих функций. Можно считать, что погрешность приближения одной функции другой функцией и есть расстояние между двумя соответствующими им точками. Иначе говоря, расстояние между исходной функцией и функцией приближения является погрешностью приближения функции функцией . Если считать, что с увеличением n степень приближения повышается, то значение расстояния между ними уменьшается. Погрешность можно выразить следующим образом [3]:

(25)

Следовательно, с ростом n, значение может только уменьшаться, но не расти. Если графически изобразить погрешность приближения разложением в ряд Фурье значений любой функции, получим кривую с переменной n, где n — число гармоник.

Эта кривая — график относительной погрешности (выражаемая в процентах), определяемая следующим образом:

,

где — мощность сигнала. Значения относительной погрешности приведены в процентах.

Из представленного графика также ясно, что с увеличением n погрешность монотонно уменьшается.

Если форма исходного сигнала гладкая, то скорость уменьшения погрешности при увеличении количества гармоник высокая. Этот случай называют хорошей сходимостью. Если сходимость хорошая, то можно восстановить исходный сигнал посредством небольшого количества гармоник, а значит, сократить объем данных. Иначе говоря, сигнал, представленный несколькими сотнями или тысячами измерений, можно приблизить всего лишь десятками значений данных или даже несколькими значениями. Этот случай наглядно представлен на рис. 14, где иллюстрируется разложение в ряд Фурье гладкого сигнала.