7 Подготовка файла данных для расчета горочной горловины

Модель горочной горловины для ввода в ЭВМ должна быть подготовлена в виде текстового файла с именем NKХХХ или NKXXX_ZZ, где ХХХ–трехзначный номер схемы, ZZ – номер варианта.

В первой строке файла указывают число точек (вершин) на спускной части горки n и число сортировочных путей m.

Во второй строке файла указывают параметры Х₁, Y_{1 ,}φ и е_min/2. В следующих n строках файла записывают списки инцидентности вершин на спускной части горки, дополненные векторами параметров Х_V. Далее в m строках файла записывают номера вершин сортировочных путей, дополненные векторами параметров Х_W

Данные в строках файла разделяют пробелами или символами табуляции (более удобно для чтения). Допускается наличие пустых строк, а также строк комментариев, начинающихся символом '*'; комментарии могут быть также в конце строк данных. Наличие комментариев не является обязательным; они облегчают работу с файлом данных.

Ниже приведен файл данных NK777 для расчета плана горочной горловины, схема которой показана на рис. 2.3.

* Файл NK777

*n m

10 7

*X1 Y1 F emin/2

0 0 0 2.4

*Примечание: расчетный путь – 6

*V Uл Uп a° a' a" Lл Lп R f

1 102 0 0 0 0 10.56 0 0 0

102 3 0 0 0 0 40.16 0 200 0

3 104 105 0 0 0 10.56 10.56 0 0

104 6 0 1 50 52 6.95 0 200 0

105 0 7 1 50 52 0 6.95 200 0

6 201 8 0 0 0 10.56 23.97 0 0

7 9 10 0 0 0 23.97 23.97 0 0

8 202 203 0 0 0 10.56 10.56 0 0

9 204 205 0 0 0 10.56 10.56 0 0

10 206 207 0 0 0 10.56 10.56 0 0

*ВУ Y R

201 35.05 200

202 29.75 200

203 24.45 200

204 19.15 200

205 13.85 200

206 8.55 200

207 3.25 200

8 Метод расчета горловины сортировочного парка

Вначале рассчитываются неизвестные углы поворота кривых на спускной части горки. Для каждого неизвестного угла нужно выбрать расчетный путь; на расчетном пути должен быть только один неизвестный угол.

Для определения неизвестного угла  на расчетном пути разработан итерационный метод, который не требует решения сложных тригонометрических уравнений и поэтому используется при автоматизации расчетов указанного угла. Сущность итерационного метода заключается в следующем. Первоначально принимается некоторое начальное значение неизвестного угла ₀ и при этом значении вычисляется ордината расчетного пути Y() как сумма проекций элементов этого пути на ось OY. С этой целью предварительно расчетный путь представляется в виде ломаной линии. При этом кривые заменяют их тангенсами; тогда длину каждого отрезка ломаной можно определить как

l_i = T_i-1 + f_{i-1, i} + T_i, (2.1)

где T_i-1, T_i - тангенсы кривых в (i-1)-й и i-й вершинах (T_i-1= ; T_i=0, т.к. R_i=0);

f_i-1,i - длина заданной прямой вставки между (i-1)-й и i-й вершинами.

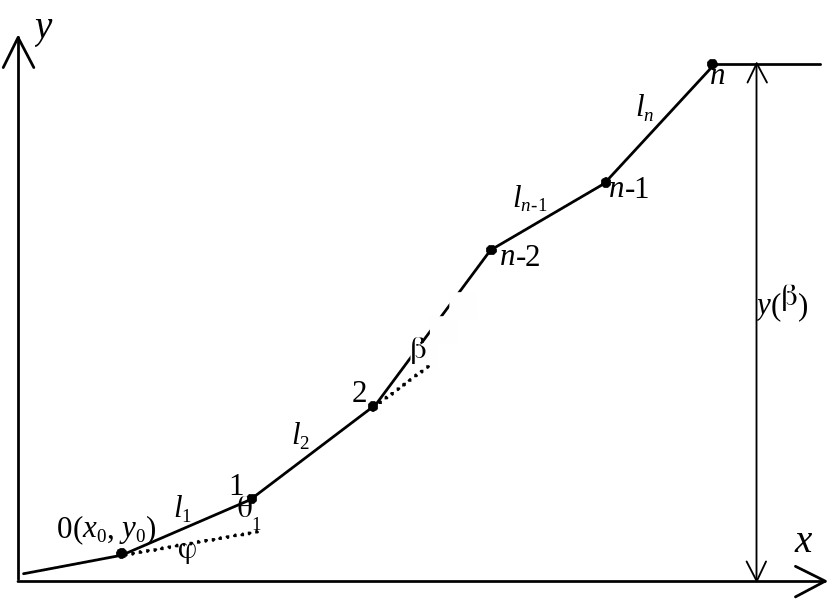
Сумма проекций элементов расчетного пути на ось oy является функцией угла :

(2.2)

где y₀ - ордината начального стрелочного перевода;

l_i - длина элемента;

_i - угол наклона элемента к оси абсцисс;

n - число элементов расчетного пути.

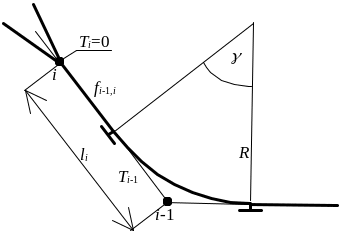
Угол наклона i-го элемента _i можно найти как алгебраическую сумму углов поворота в точках расчетного пути

(2.3)

где  - угол наклона базисного элемента;

_j - угол поворота расчетного пути в j-й точке.

Таким образом, при некотором начальном значении ₀ неизвестного угла  с помощью приведенных выражений можно вычислить величину y(₀). Вычисленное значение у(₀) сравнивается с ординатой расчетного пути Y и в зависимости от результатов сравнения изменяется на заданную величину (шаг итерации) предыдущее значение угла :

_k+1 = _k + sign(Y - y(_k)), k = 0, 1, 2,…

Указанная процедура повторяется до тех пор, пока не будет найден интервал [__k+1], в котором величина Y - y() меняет знак. После этого поиск угла осуществляется внутри указанного интервала методом половинного деления; расчеты завершаются при выполнении условия

Y - y (_k)- ,

где  - требуемая точность определения ординаты расчетного пути.

При найденном значении неизвестного угла  с помощью приведенных выражений определяются координаты x_i, y_i всех точек расчетного пути.

На остальных путях, маршрут на которые от вершины горки проходит через найденный угол , определяются прямые вставки между крестовиной последней стрелки и вершиной угла поворота

Следует заметить, что в горочной горловине может быть несколько неизвестных углов, для каждого из которых должен быть задан отдельный расчетный путь; расчет указанных углов осуществляется поочередно.

В качестве расчетного можно выбрать любой путь горловины. Обычно выбирают один из крайних путей пучка (если пучок полный) или соседний с крайним (если пучок неполный). При этом целесообразно сделать несколько вариантов расчета при разных расчетных путях и выбрать лучший по условиям вписывания кривых на всех сортировочных путях.

При проектировании соединительных кривых на сортировочных путях, не являющихся расчетными, могут возникнуть определенные трудности. В частности, для некоторых смежных путей ширина междупутья меньше минимальной величины e_min (см. рис.___, пути 2-3). В этом случае на пути 2 укладывается дополнительная обратная кривая с углом поворота . По тем же соображениям на пути 3 одну соединительную кривую заменяют двумя кривыми одного направления. Вершине угла дополнительной кривой автоматически присваивается тот же номер, который имеет основная кривая на том же пути, но с первой цифрой 3.

Следует заметить, что задачу выбора оптимальных параметров соединительных кривых нельзя решать для отдельно взятого пути, поскольку его положение влияет на ширину междупутий со смежными путями. Ее необходимо решать, как минимум, для отдельного пучка путей. При этом необходимо стремиться к тому, чтобы максимальное расстояние L_i от головной стрелки пучка до точки возможной установки замедлителей на путях пучка было наименьшим . Поскольку замедлители в пучке укладывают в створе, их выравнивают по наиболее удаленной точке пучка.

Для приближенного решения данной задачи используется интерактивный режим проектирования плана сортировочных путей. В этом режиме имеется возможность поочередного изменения четырех указанных переменных f₁, , R₁, R₂. После каждого изменения по текущим значениям этих параметров автоматически рассчитывается вставка f₂. При этом на экране дисплея соответственно изменяется план проектируемого пути. При необходимости процедура корректирования параметров каждого пути может повторяться многократно.

Для удобства выбора рациональной конструкции плана пути на экран дисплея выводятся точки, в которых ширина междупутья достаточна для укладки парковых замедлителей.

Точка, в которой расстояния до двух соседних путей равны e_min/2, определяется как точка пересечения эквидистант – линий, расположенных на одинаковом расстоянии e_min/2 от соответствующих путей. Указанные точки отображаются на дисплее; их положение корректируется после каждого изменения значений параметров соединительных кривых некоторого пути.