2º. Классификация квадрик в трёхмерном евклидовом пространстве

Дадим полную классификацию квадрик в пространстве Е₃ , для этого рассмотрим все частные случаи упрощения уравнения (6). .

Случай 1: m=n=3 , p ≠ 0.

Уравнение (6) принимает вид:

или

.

В зависимости от знаков чисел p₁, p₂, p₃ и p уравнение принимает различные виды.

а) – эллипсоид.

Так как не всякие два эллипсоидаравны и даже подобны, в евклидовой геометрии (см. опр. (3) §14) имеется возможность классификации эллипсоидов и других квадрик (при n=3 поверхностей 2-го порядка). Если a≠ b≠ c, то эллипсоид называется трёхосным. Если равны какие - либо две из чисел a, b, c, то имеем эллипсоид вращения. Если же a=b=c, то эллипсоид является сферой. Эта классификация инвариантна относительно движений пространства E_n .

б) – мнимый эллипсоид.

в) – однополостный гиперболоид (при a=b - о.г. вращения).

г) - двуполостный гиперболоид (при a=с – д.г. вращения).

Случай 2: m=n=3, p=0.

Уравнение (6) принимает вид:

Возможны частные случаи:

а) – конус (при a=b – конус вращения).

б) – мнимый конус с вершиной в начале координат.

Случай 3: n=3, m=2, d₃≠0.

Уравнение (6) принимает вид:

. .

Освободимся от свободного члена p с помощью параллельного переноса системы координат по формулам:

Получим уравнение: и его частные случаи:

а) – эллиптический параболоид (при a=b – э.п. вращения).

б) – гиперболический параболоид (или седловая поверхность).

Случай 4 (цилиндры 2-го порядка):

I. .

а) - эллиптический цилиндр (при - цилиндр вращения или

прямой круговой цилиндр).

б) - мнимый эллиптический цилиндр .

в) - гиперболический цилиндр.

II.

а) - пара пересекающихся по оси плоскостей.

б) - пара мнимых плоскостей, пересекающихся по оси .

III.

а) - пара различных параллельных плоскостей.

б) - пара мнимых параллельных плоскостей.

в) - пара совпавших с плоскостью плоскостей.

IV. где

то есть d₂ и d₃ не равны нулю одновременно,

Разделим обе части этого уравнения на p₁ ≠0 и освободимся, как и в случае (3), от свободного члена p:

Обозначим и выполним ортогональное преобразование переменных (проверить!) по формулам:

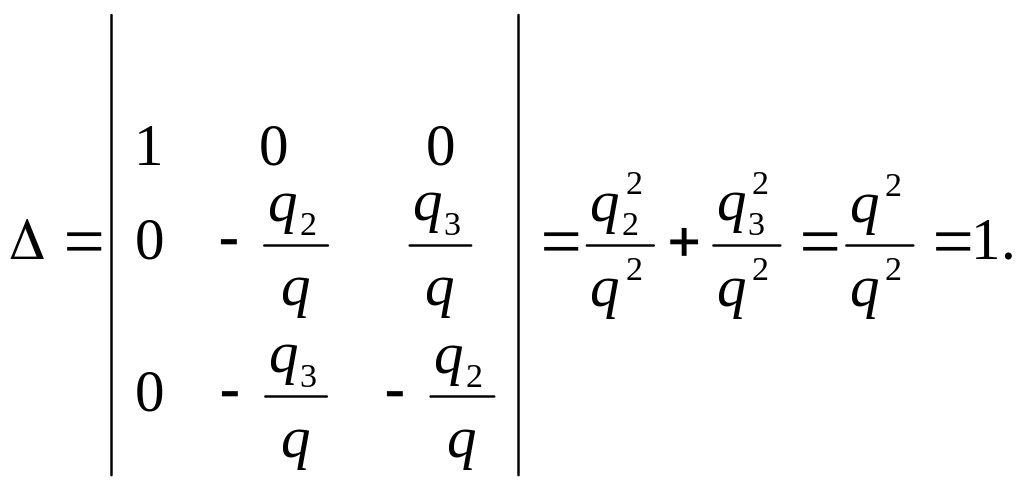
Оно означает переход к новой прямоугольной декартовой системе координат, относительно которой квадрика будет иметь уравнение:

– параболический цилиндр.

Замечание 2: подсчёт получившихся канонических или простейших уравнений показывает, что в пространстве E₃ существует семнадцать различных видов поверхностей 2-го порядка.

§ 25. Проективное пространство, его плоскости и прямые

Выберем в действительном n+1 -мерном аффинном пространстве А_n+1 точку О и рассмотрим множество всех проходящих через точку О прямых, двумерных плоскостей, трёхмерных плоскостей, ... , n-мерных плоскостей (гиперплоскостей пространства А_n+1). Назовем это множество связкой с центром О в пространстве А_n+1 и будем обозначать его одной буквой О. Установим между различными элементами связки, т.е. её прямыми, двумерными плоскостями, ..., (к+1)-мерными плоскостями, отношения инцидентности или взаимной принадлежности следующим образом:

k-мерная плоскость инцидентна (к+1)-мерной плоскости, если она содержится в ней.

Отношение инцидентности симметрично: если прямая d инцидентна плоскости , то говорят, что и плоскость инцидентна прямой d. Прямые связки О будем также называть ее лучами.

Опр. 1. Связку О пространства А_n+1 назовём действительным n-мерным проективным пространством и обозначим RPⁿ, соответственно переименовывая лучи, …, (к+1)-мерные плоскости связки в точке, ..., k-мерные плоскости проективного пространства RPⁿ (размерность уменьшая на 1).

Опр. 2. Аффинная система координат пространства А_n+1, начало которой совпадает с центром данной связки, называется аффинной координатной системой связки О.

Опр. 3. Любая упорядоченная последовательность из n+1 чисел х₁, х₂, ... , х_n+1, являющаяся координатами какого-либо направляющего вектора и данного луча m связки О, называется набором координат луча m в аффинной системе координат .

Замечание 1. Очевидно, набор, состоящий из одних лучей, является запрещенным и не рассматривается ( не имеет направления). Кроме того, все наборы координат луча m образуют класс пропорциональных между собой числовых наборов и, обратно, всякий класс пропорциональных между собой числовых наборов из n+1 чисел х₁,х₂, ..., х_n+1 является классом наборов координат некоторого луча m связки О относительно данной системы координат .

Отождествим каждый луч m связки О с классом наборов его координат относительно фиксированной аффинной системы координат . Тем самым мы приходим к понятию арифметического проективного пространства. Его точками являются всевозможные классы пропорциональных между собой наборов из n+1 чисел: если ( х₁,х₂, ..., х_n+1) || m, то M( х₁,х₂, ..., х_n+1) и обратно.

Опр. 4. Назовём гиперплоскостью, т.е. (n-1)-мерной плоскостью проективного пространства RPⁿ, множество точек M(х₁,х₂,..., х_n+1), координаты которых удовлетворяют линейному однородному уравнению

, (1)

где коэффициенты u₁,u₂, ..., u_n+1 определены с точностью до общего числового множителя и называются координатами данной гиперплоскости.

Опр. 5. Множество точек M(х₁,х₂,...,х_n+1), координаты которых удовлетворяют системе из n-r линейно независимых однородных уравнений вида:

(2)

называется r-мерной плоскостью n-мерного проективного пространства RPⁿ или коротко r-плоскостью. Ранг матрицы системы (2) равен n+l-(n-r) = г+1, значит, все её решения являются линейными комбинациями каких-нибудь независимых решений ,где .

Это позволяет получить параметрические уравнения r-плоскости:

(3)

где параметры независимо друг от друга всевозможные действительные значения.

В частности, параметрическое представление прямой в пространстве RPⁿ имеет вид:

, где , P(p₁,p₂,...,p_n+1) и Q(q₁,q₂,...,q_n+1) -некоторые её фиксированные точки, а числа и пробегают всевозможные числовые значения, кроме запрещенной пары .

Замечание 2. Множество всех гиперплоскостей n-мерного арифметического проективного пространства, а также множество всех его точек, находится в биективном соответствии с множеством всех классов, состоящих из пропорциональных между собой наборов из n+1 чисел. Точка то M( х₁,х₂, ..., х_n+1) и гиперплоскость (u₁,u₂, ..., u_n+1) инцидентны, если .

Между точками и гиперплоскостями проективного пространства имеется равноправие, выражающееся в следующем принципе (от PRINCIPIUM - (лат.) - основное, исходное положение какой-либо теории или учения).

Принцип двойственности: если верно какое-нибудь утверждение об инцидентности точек и гиперплоскостей проективного пространства, то при замене в данном предложении слова «точка» словом «гиперплоскость» и наоборот и сохранении инцидентности получается также верное утверждение *, двойственное утверждению .

Например, для проективной плоскости при n=2 имеем : «любой прямой инцидентно бесконечно много точек», *: «любой точке инцидентно бесконечно много прямых».