3º. Ортогональные инварианты

Подвергнем переменные в квадратичной форме f ортогональному преобразованию и будем рассматривать его как переход к новому ортонормированному базису евклидова векторного пространства . При этом преобразовании у линейного оператора, матрица которого совпадает с матрицей квадратичной формы, остаются неизменными коэффициенты характеристического многочлена. Они являются функциями элементов такой матрицы или равных им соответственно коэффициентов квадратичной формы. Так как эти выражения (функции) не меняются при ортогональном преобразовании, то они называются ортогональными инвариантами квадратичной формы.

Пример:

- характеристический многочлен линейного оператора, матрица которого совпадает с матрицей квадратичной формы.

Выражения - ортогональные инварианты квадратичной формы. Значит и корни характеристического многочлена также являются ее ортогональными инвариантами.

§24. Квадрики в евклидовом пространстве

1º. Упрощение уравнения квадрики

Определение квадрики, данное в §20 для аффинного пространства , сохраняется и для евклидова пространства . Но теперь уже используется только прямоугольные декартовы системы координат.

Пусть квадрика задана относительно ортонормированной системы координат общим уравнением вида: (1), где

Вначале производится линейное ортогональное преобразование переменных приводящее к каноническому виду квадратичную форму из левой части уравнения (1) (см. §23). Пусть оно имеет вид: (2), где .

С геометрической точки зрения это означает переход к новой прямоугольной декартовой системе координат, получаемой из исходной с помощью вращения вокруг начала координат. Уравнение (1) квадрики примет вид:

(3)

где и коэффициенты не равны нулю.

Выделим полные квадраты:

(4)

Подвергнем систему координат параллельному переносу

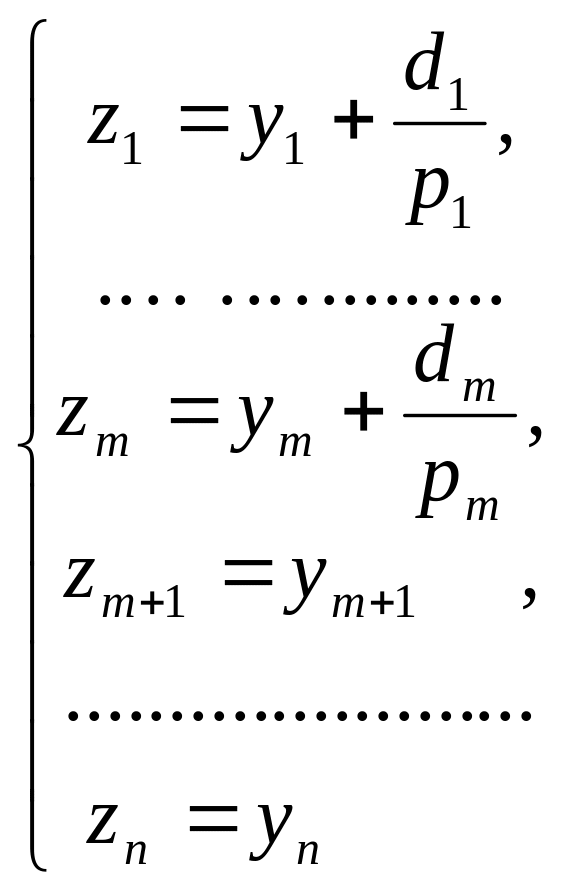(5) - это ортогональное преобразование ( ).

Вводя обозначение , получаем уравнение квадрики в новой ортонормированной системе координат:

, (6)

где и коэффициенты отличны от нуля.

При дальнейшем упрощении этого уравнения в общем случае уже не удается добиться того, чтобы все коэффициенты при квадратах координат были равны , так как при помощи отрицательного преобразования квадратичная форма не всегда приводится к нормальному виду. Поэтому в пространстве E_n уравнение квадрики в общем случае уже не удается привести к такому простому виду, как в пространстве A_n (нормальному виду).

Замечание 1: так как равные фигуры является также аффинно-эквивалентными, то проведённая в §21 аффинная классификация квадрик имеет место и в пространстве E_n . Однако не всякие аффинно-эквивалентные фигуры равны, поэтому каждый класс аффинной классификации разбивается на бесконечное множество классов так, что любые две квадрики из одного класса равны, а любые две квадрики из разных классов не равны. То есть в пространстве E_n появляются новые виды квадрик, отсутствующие в пространстве А_n .