§21.Классификация квадрик в пространстве An

1. Эллипсоиды и гиперболоиды

Уравнение (2) из §20 при m=n принимает вид:

, (1)

Числа равны .

В зависимости от знаков получаются квадрики разных видов.

1) При квадрика называется эллиптической и имеет уравнение .

Замечание 1: В аффинной геометрии отсутствует понятие расстояния между точками, поэтому нет и понятия сферы и эллипсоида вращения.

2) При уравнение (1) имеет вид: и определяет пустое множество точек, но по аналогии с предыдущем случаем называется мнимым эллипсоидом.

3) Если числа не все одинаковы, то квадрика называется гиперболоидом.

Замечание 2: Согласно теореме (2) из §20 эллипсоиды и гиперболоиды с уравнением (1) являются центральными квадриками; их центр совпадает с началом координат.

Примеры:

1) n=1

Для аффинной прямой A₁ имеем уравнение и , задающие соответственно пару точек и пустое множество.

2) n=2, квадрики аффинной плоскости:

- эллипс

- мнимый эллипс

- гиперболы, взаимно сопряжённые.

3) n=3, квадрики пространства :

- эллипсоид

- мнимый эллипсоид

- однополостный гиперболоид

- двуполостный гиперболоид

В остальных случаях следует изменить нумерацию координат.

2. Конические квадрики (конусы)

Уравнение (3) из §20 при m=n принимает вид:

(2)

где все равны .

1. Если значения не все одинаковы, то квадрика называется конусом. Это центральная квадрика, её центр совпадает с началом координат и называется вершиной.

Замечание 3: Если координаты точки , отличной от вершины конуса, удовлетворяют уравнению (2), то ему удовлетворяют так же координаты любой точки вида , . Множество всех таких точек является прямой, проходящей через точку A и вершину конуса – начало координат. Эта прямая называется его прямолинейной образующей.

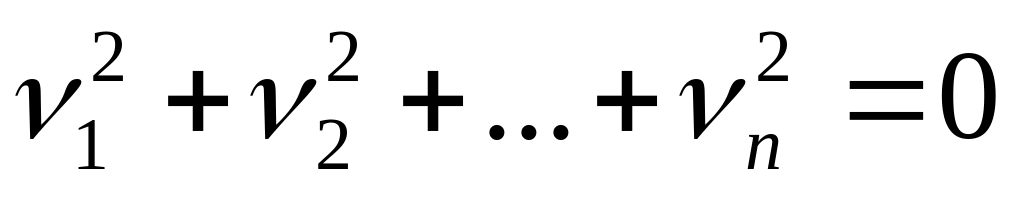2. Если , то имеем уравнение . Квадрика состоит, лишь из одной точки (начало координат) и называется мнимым конусом с вершиной в этой точке.

Примеры:

4) n=1: - пара точек аффинной прямой , совпадающих с началом координат.

5) n=2, квадрики аффинной плоскости .

или - пара пересекающихся в начале координат прямых.

или , - пара мнимых прямых, пересекающихся в действительной точке .

6) n=3, квадрики пространства

- мнимый конус (точка О),

- конус (с вершиной в точке О).

III. Параболоиды.

Уравнение (4) из §20 при m=n-1 принимает вид:

(3)

где все равны .

Квадрика называется параболоидом, она не имеет ни одного центра (является нецентральной), что вытекает из замечания (2) §20.

Примеры:

7) n=2, уравнение задаёт на аффинной плоскости параболу с вершиной и осью , .

Аналогично при имеем параболу .

8) n=3, поверхности пространства :

- эллиптический параболоид

- гиперболический параболоид

( ; )

IV. Цилиндрические квадрики (цилиндры)

Рассмотрим теперь случаи, когда в уравнениях (2) и (3) из §20 m<n, а в уравнении (4) из §20 m<n-1. Положим в уравнении (2) и (3) m=r, а в уравнении (4) m=r-1. Получим следующие уравнения:

(4)

(5)

(6)

где r<n и все равны .

Квадрики с такими уравнениями называются цилиндрическими (цилиндрами).

Замечание 4: Можно показать, что цилиндрическая квадрика состоит из параллельных друг другу (n-r) – мерных плоскостей, называемых образующими, пересекающих некоторую квадрику, называемую направляющей и лежащей в r – мерной плоскости . Квадрики с уравнениями (4) и (5) имеют бесконечное множество центров, являющееся (n-r)-мерной плоскостью. Так как переменная содержится в уравнении в первой степени, изменение её знака приводит к другому уравнению, следовательно, (6) центров не имеет.

Примеры:

9) n=2, линии аффинной плоскости :

- пара различных параллельных оси прямых. Образующими являются две прямые с уравнениями и , а направляющие – пара точек A(1;0) и B(-1;0), в которых эти прямые пересекают ось с уравнением .

- пара мнимых прямых, параллельных оси .

10) n=3, поверхности пространства .

- эллиптический цилиндр.

- мнимый эллиптический цилиндр.

- гиперболический цилиндр.

- параболический цилиндр.

- пара пересекающихся плоскостей.

- пара мнимых плоскостей, пересекающихся по действительной прямой с уравнениями .

- пара различных параллельных плоскостей.

- пара мнимых параллельных плоскостей.

- пара совпадающих плоскостей.

Остальные случаи сводятся к рассмотренным изменением нумерации координат.

Замечание 5: Сопоставление рассмотренных выше примеров показывает, что все квадрики пространства разбивается на три класса, пространства - на девять классов, пространства - на семнадцать классов. В один класс при этом объединяются все квадрики, уравнения которых с помощью надлежащего выбора аффинной системы координат можно привести к одинаковому виду. Любые две квадрики одного класса аффинно-эквивалентны, так как формулы перехода от одной системы координат к другой и формулы аффинного преобразования пространства с алгебраической точки зрения имеют один и тот же вид.

Замечание 6: Квадрики с различными нормальными уравнениями могут оказаться одинаковыми точечными множествами. Например, мнимый эллипс и пара мнимых параллельных прямых – пустое точечное множество. Поэтому аффинно-эквивалентными могут оказаться и квадрики из различных классов. С геометрической точки зрения эти классы не различаются между собой.