Глава 10. Рынки активов

1. Вы, бизнес-менеджер Буньян Форестс Инкорпорейтед, принимаете решение о том, следует ли вам рубить деревья. Рыночная стоимость лесоматериалов, которую вы выручите, если позволите деревьям расти до возраста t лет, задана функцией

Г-н Буньян может заработать на процентах 5% в год, положив деньги в банк. Темп роста рыночной стоимости деревьев будет превышать 5% до тех пор, пока деревья не достигнут _____ -летнего возраста.

a) Если г-н Буньян заинтересован в деревьях как в инвестиции, до какого возраста он должен позволить им вырасти?_______________________

b) В каком возрасте деревья имеют наибольшую рыночную стоимость?__________________________

2. Вы предполагаете, что цена некоторой картины будет подниматься на 8% в год в течение неограниченного периода. Рыночная процентная ставка составляет 10%. Допустим, что отсутствуют затраты на брокерское вознаграждение при покупке или продаже.

(а) Если вы платите цену х долларов за картину теперь и продаете её через год, во сколько вам обойдется то, что вы держите у себя картину вместо того, чтобы дать взаймы х долларов под рыночную кредитную ставку?__________

(b) Вы согласны были бы заплатить 100 долларов в год за то, чтобы картина висела у вас на стене. Напишите уравнение, которое можно решить относительно цены х, за которую вы согласны были бы купить картину. _________________________________________________________________

(с) За какую цену вы согласились бы купить картину?____________________

Глава 11. Неопределенность

1 . Вилли является владельцем маленькой шоколадной фабрики, расположенной близко к реке, которая иногда разливается весной с разрушительными последствиями. Следующим летом Вилли планирует продать фабрику и уйти на пенсию. Единственный доход, который у него будет – это выручка от продажи фабрики. Если наводнения не будет, его фабрика будет стоить 500 тыс. долл. Если случится наводнение, тогда то, что останется от его фабрики, будет стоить только 50 тыс. долл. Вилли может купить страховку от наводнения с затратами 0,1 долл. на каждый 1 долл. Страховой выплаты. Он полагает, что вероятность наводнения этой весной 1/10. Пусть c_F означает условное благо «доллары, если есть наводнение», а c_NF означает условное благо «доллары, если наводнения нет».

Функция полезности фон Неймана-Моргенштерна для Вилли имеет вид: U(c_F, c_NF) = 0,1( c_F) ^½, + 0,9 (c_NF) ^½

а) Если он не покупает страховку, тогда при наступлении любого из случаев потребление Вилли будет равно стоимости фабрики, таким образом его набор случайных благ будет (c_F, c_NF) = ____________________________

б) Чтобы купить страховку, по которой ему будет выплачиваться х долл. в случае наводнения, Вилли должен платить страховую премию 0,1х. (Страховая премия должна уплачиваться вне зависимости от того, будет потоп или нет.) Если Вилли будет застрахован на х долл., тогда, если случится наводнение, он получит х долл. страхового пособия. Предположим, что Вилли заключил страховой договор на случай наводнения на х долл. Тогда после уплаты страховой премии его потребление составит с_F = ________________ . Если Вилли заключил страховой договор на эту сумму и наводнения не произошло, тогда его потребление составит с_NF = ______________________________________ __________________________.

в) Вы можете убрать х из 2 уравнений, получив тем самым уравнение с 2 переменными с_F и с_NF. Таким образом вы найдёте уравнение бюджетной линии для Вилли. Данное уравнение может быть преобразовано в различные формы, путём умножение каждого члена уравнения на положительное число. Тогда, если принять «цену» c_NA за единицу, то уравнение примет вид

0,9 с_NF + ____ с_{F =} ____________________________________.

г) Предельная норма замещения Вилли между 2 случайными наборами, долларами, если не будет наводнения и долларами, если будет наводнение равна . Для того чтобы найти оптимальную точку выбора нашего героя необходимо приравнять MRS к числу _______________.

Решив это равенство вы найдёте, что Вилли выбрал потреблять случайные наборы в соотношении с_NF= с_F .

д) Поскольку мы знаем соотношение, в котором Вилли будет потреблять с_NF и с_F в точке выбора, и нам известно его бюджетное уравнение, то без труда, объединив их в систему, мы найдём, что оптимальный выбор для нашего героя таков (с_F , с_NF ) = ______________________________________________

Получается, что Вилли предпочтёт купить страховку, по которой он получит ___________________ в случае наводнения. Размер страховой премии, который должен заплатить наш герой равен ____________________________.

2. Функция ожидаемой полезности Билли Джонса описывается уравнением u(c)=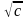 . Билли является выпускником профессионального футбольного колледжа. Ему предложили контракт стоимостью 1000000$, который полностью выплатят, если он не будет травмирован во время игр. Если он будет травмирован, то ему выплатят 10000$, чтобы ему хватило на обратную дорогу домой и восстановление. Предположим, что существует 10% вероятность того, что билли будет травмирован во время игры.

а) Рассчитайте ожидаемую полезность контракта Билли _______________

б) Если Билли заплатит р$ и застрахует свое здоровье, то ему выплатят 1000000$ при наступлении несчастного случая. Так он может быть уверен, что получит 1000000 – р не зависимо от того, что с ним случится. Запишите уравнение, показывающее какую максимальную сумму готов заплатить Билли за свою страховку?___________________________________________

в) Решите это уравнение относительно р ____________________________