
- •Требования к программе статистического наблюдения:
- •9.Виды статистических таблиц
- •6.7. Динамика производства контрольно-кассовых машин в России в 2006-2011 гг.
- •14. 3.5. Основные правила построения статистических графиков
- •3.6. Анализ графиков
- •16. Виды относительных величин
- •19. Средние величины и показатели вариации
- •22. Средняя арифметическая простая
- •2. Размах вариации. Среднее линейное отклонение
- •3. Дисперсия. Виды дисперсий
- •4. Среднее квадратическое (стандартное) отклонение. Коэффициент вариации
- •5. Структурные показатели вариационного ряда: мода, медиана, квартили, децили
- •6. Показатели дифференциации
- •Определение моды и медианы по несгруппированным данным
- •33. Индивидуальные индексы
- •4. Системы индексов.
- •5. Индексы структурных сдвигов.
- •6. Индексы пространственно-территориального сопоставления.
- •7. Важнейшие экономические индексы и их взаимосвязи.
- •2.3. Средний гармонический индекс.
- •36. Предмет, метод и задачи статистики промышленности.
- •42???. Взаимосвязь стоимостных показателей объема продукции
- •1. Статистика состава работников
- •2. Показатели движения трудовых ресурсов и использования рабочего времени
- •3. Статистика рабочего времени
- •Коэффициент использования числа дней работы на одного работника в году
- •Коэффициент использования продолжительности 1 рабочего дня в человеко-часах
- •Различаются следующие виды стоимостной оценки основных фондов:
- •3. Использование основных фондов
- •5. Статистика научно-технического прогресса
- •1. Понятие себестоимости и классификация затрат.
- •2. Классификация затрат по экономическим элементам.
- •3. Классификация затрат по статьям калькуляции.
- •2. Классификация затрат по экономическим элементам.
- •3. Классификация затрат по статьям калькуляции.
22. Средняя арифметическая простая
Простая среднеарифметическая величина представляет собой среднее слагаемое, при определении которого общий объем данного признака всовокупности данных поровну распределяется между всеми единицами, входящими в данную совокупность. Так, среднегодовая выработка продукции на одного работающего — это такая величина объема продукции, которая приходилась бы на каждого работника, если бы весь объем выпущенной продукции в одинаковой степени распределялся между всеми сотрудниками организации. Среднеарифметическая простая величина исчисляется по формуле:
![]()
Простая средняя арифметическая — Равна отношению суммы индивидуальных значений признака к количеству признаков в совокупности
![]()
Пример 1. Бригада из 6 рабочих получает в месяц 3 3,2 3,3 3,5 3,8 3,1 тыс.руб.
Найти среднюю заработную плату Решение: (3 + 3,2 + 3,3 +3,5 + 3,8 + 3,1) / 6 = 3,32 тыс. руб.
Средняя арифметическая взвешенная
Если объем совокупности данных большой и представляет собой ряд распределения, то исчисляется взвешенная среднеарифметическая величина. Так определяют средневзвешенную цену за единицу продукции: общую стоимость продукции (сумму произведений ее количества на цену единицы продукции) делят на суммарное количество продукции.
Представим это в виде следующей формулы:
![]()
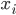 —
цена
за единицу продукции;
—
цена
за единицу продукции;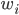 —
количество
(объем) продукции;
—
количество
(объем) продукции;
Взвешенная средняя арифметическая — равна отношению (суммы произведений значения признака к частоте повторения данного признака) к (сумме частот всех признаков).Используется, когда варианты исследуемой совокупности встречаются неодинаковое количество раз.
Пример 2. Найти среднюю заработную плату рабочих цеха за месяц
Заработная плата одного рабочего тыс.руб; X |
Число рабочих F |
3,2 |
20 |
3,3 |
35 |
3,4 |
14 |
4,0 |
6 |
Итого: |
75 |
Средняя заработная плата может быть получена путем деления общей суммы заработной платы на общее число рабочих:
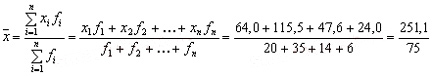
Ответ: 3,35 тыс.руб.
Средняя арифметическая для интервального ряда
При расчете средней арифметической для интервального вариационного ряда сначала определяют среднюю для каждого интервала, как полусумму верхней и нижней границ, а затем — среднюю всего ряда. В случае открытых интервалов значение нижнего или верхнего интервала определяется по величине интервалов, примыкающих к ним.
Средние, вычисляемые из интервальных рядов являются приближенными.
Пример 3. Определить средний возраст студентов вечернего отделения.
Возраст в годах !!х?? |
Число
студентов
|
Среднее
значение интервала
|
Произведение
середины интервала (возраст)
на
число студентов |
до 20 |
65 |
(18 + 20) / 2 =19 18 в данном случае граница нижнего интервала. Вычисляется как 20 — (22-20) |
1235 |
20 — 22 |
125 |
(20 + 22) / 2 = 21 |
2625 |
22 — 26 |
190 |
(22 + 26) / 2 = 24 |
4560 |
26 — 30 |
80 |
(26 + 30) / 2 = 28 |
2240 |
30 и более |
40 |
(30 + 34) / 2 = 32 |
1280 |
Итого |
500 |
|
11940 |

Средние, вычисляемые из интервальных рядов являются приближенными. Степень их приближения зависит от того, в какой мере фактическое распределение единиц совокупности внутри интервала приближается к равномерному.
При расчете средних в качестве весов могут использоваться не только абсолютные, но и относительные величины (частость):
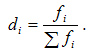
Средняя арифметическая обладает целым рядом свойств, которые более полно раскрывают ее сущность и упрощают расчет:
1. Произведение средней на сумму частот всегда равно сумме произведений вариант на частоты, т.е.
![]()
2.Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических этих величин:
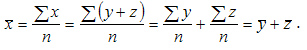
3.Алгебраическая сумма отклонений индивидуальных значений признака от средней равна нулю:
![]()
4.Сумма
квадратов отклонений вариантов от
средней меньше, чем сумма квадратов
отклонений от любой другой произвольной
величины ![]() ,
т.е:
,
т.е:
![]()
5. Если все варианты ряда уменьшить или увеличить на одно и то же число , то средняя уменьшится на это же число :
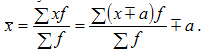
6.Если
все варианты ряда уменьшить или увеличить
в ![]() раз,
то средняя также уменьшится или увеличится
в
раз:
раз,
то средняя также уменьшится или увеличится
в
раз:

7.Если
все частоты (веса) увеличить или уменьшить
в ![]() раз,
то средняя арифметическая не изменится:
раз,
то средняя арифметическая не изменится:
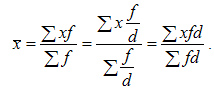

23. Вариационными называют ряды распределения, построенные по количественному признаку. Значения количественных признаков у отдельных единиц совокупности непостоянны, более или менее различаются между собой.
Вариация - колеблемость, изменяемость величины признака у единиц совокупности. Отдельные числовые значения признака, встречающиеся в изучаемой совокупности, называют вариантами значений. Недостаточность средней величины для полной характеристики совокупности заставляет дополнять средние величины показателями, позволяющими оценить типичность этих средних путем измерения колеблемости (вариации) изучаемого признака.
Наличие вариации обусловлено влиянием большого числа факторов на формирование уровня признака. Эти факторы действуют с неодинаковой силой и в разных направлениях. Для описания меры изменчивости признаков используют показатели вариации.
Задачи статистического изучения вариации:
1) изучение характера и степени вариации признаков у отдельных единиц совокупности;
2) определение роли отдельных факторов или их групп в вариации тех или иных признаков совокупности.
В статистике применяются специальные методы исследования вариации, основанные на использовании системы показателей, спомощью которых измеряется вариация.
Исследование вариаций имеет важное значение. Измерение вариаций необходимо при проведении выборочного наблюдения, корреляционном и дисперсионном анализе и т. д.
По степени вариации можно судить об однородности совокупности, об устойчивости отдельных значений признаков и типичности средней. На их основе разрабатываются показатели тесноты связи между признаками, показатели оценки точности выборочного наблюдения.
Различают вариацию в пространстве и вариацию во времени.
Под вариацией в пространстве понимают колеблемость значений признака у единиц совокупности, представляющих отдельные территории. Под вариацией во времени подразумевают изменение значений признака в различные периоды времени.
Для изучения вариации в рядах распределения проводят расположение всех вариантов значений признака в возрастающем или убывающем порядке. Этот процесс называют ранжированием ряда.
Самыми простыми признаками вариации являются минимум и максимум - самое наименьшее и наибольшее значение признака в совокупности. Число повторений отдельных вариантов значений признаков называют частотой повторения (fi). Частоты удобно заменять частостями – wi. Частость - относительный показатель частоты, который может быть выражен в долях единицы или процентах и позволяет сопоставлять вариационные ряды с различным числом наблюдений. Выражается формулой:
![]()
Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение. К относительным показателям колеблемости относят коэффициент осцилляции, относительное линейное отклонение, коэффициент вариации.
